停业了很久,雀氏对不起37个忠实粉丝,尽量保持不塌房。
言归正传,最近在写分支定界求TSP的一个小项目,涉及到图和树的各种知识,就浅浅的从无向图的遍历开始总结一下近期的学习工作,使用DFS的递归遍历无向图。
邻接矩阵、邻接表等都可以用来表示一张图,这里使用邻接表数组来表示,即以顶点为索引的列表数组,具体实现使用字典来创建邻接表数组。
graph = {0:[1,2],1:[0,3,4],2:[0,3],3:[1,2,5],4:[1,3,6],5:[3,6],6:[4,5]}
深度优先搜索DFS简单地来说,就是在访问其中一个顶点时,将它标记为已访问,递归的访问它所有没有被标记的相邻顶点。
老习惯,上代码。
def dfs(graph,s,visited):#输入 :无向图Graph,起始顶点s,已经标记的顶点visited []visited.append(s)for v in graph[s]:if v not in visited:dfs(graph,v,visited)
运行看结果。
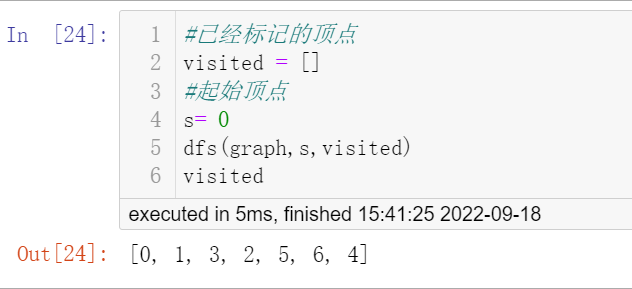
浅浅的分析一下递归的过程
graph = {0:[1,2],1:[0,3,4],2:[0,3],3:[1,2,5],4:[1,3,6],5:[3,6],6:[4,5]}def dfs(graph,s,visited):#输入 :无向图Graph,起始顶点s,已经标记的顶点visited []visited.append(s)for v in graph[s]:if v not in visited:dfs(graph,v,visited)
dfs(0) ---dfs(1)---0已经被标记了,下一个dfs(3)---1已经被标记了,所以下一个dfs(2)---graph[2]里的0,3都被标记了,回到graph[3],接着dfs(5)--3已经被标记了,所以dfs(6)---接下来就简单了,dfs(4)。好像就结束了应该是这样吧。
到这里如果就结束的话,显得敷衍,折腾了一下,实现了一个简单有点笨的s-v的路径构建的功能,还是用上面的例子来说明,最后visited = [0,1,3,2,5,6,4],根据这个标记顺序,会有且仅有0-1,1-3,3-2,3-5,5-6,6-4被选中(别问为什么,这是我的规则)。
def construct_path(G,u,v,visited):path = []if v in visited:#逆序求v-u的路径path.append(v)cur = v#如果找到了u,说明已经找到起点了,可以停止了while cur != u:#获取当前顶点的前一个被标记节点prepre = visited[visited.index(cur)-1]#如果pre在当前顶点cur的列表中#换句人说的话,pre和cur是直连的,并且被pre-cur被标记了if pre in G[cur]:path.append(pre)cur = pre#将路径v-u逆序,得到路径u-vpath.reverse()return path#构建0到5的路径 u = 0,v = 5construct_path(G,0,5,visited)#output : [0,1,3,5]
首先运行前面的dfs,得到 visited = [0,1,3,2,5,6,4],根据这个标记顺序,会有且仅有0-1,1-3,3-2,3-5,5-6,6-4被选中(别问为什么,这是我的规则)。看第4和5行,将构建u-v的路径转为构建v-u的路径。会有人好奇为啥0到5的路径为啥不是0-3-5这条,因为0-3没有被标记啊!至于为什么,这就是我的规则,别管(懂的自然会懂我的心路历程,不懂就算,反正构建路径又不对成本、距离等做要求)。
好了,这期就先到这里,下期打算做一个并查集union-find和最小生成树的联合。






