以木材切割为例讲解列生成法Column Generation(附Python代码）

前言

列生成法是一种用于求解大规模线性优化问题的算法，本质上是单纯形法的一种，所不同的是列生成法改善了大规模优化问题中单纯形法中基变换计算效率低的问题，在整数规划中已得到广泛应用。

因为是难度比较大的一个方法，默认读者具有一点点的先验知识，运筹学（线性规划及其对偶问题），矩阵(矩阵的逆和乘法)，真的就yi点点。

先带大家回顾，（1）线性规划问题的最优性判断和对偶理论；（2）列生成的理论知识；（3）最后上代码和结合例子分析。

最优性判断

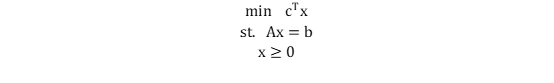
对偶理论

列生成Column Generation

列生成法是一种用于求解大规模线性优化问题的算法，本质上是单纯形法的一种，所不同的是列生成法改善了大规模优化问题中单纯形法中基变换计算效率低的问题，在整数规划中已得到广泛应用。

       列生成适用于解决变量很多但是约束相对较少的问题(反过来的话，可以考虑一下Benders,以后再分享)。列生成的思路是主问题(Master Problem,MP)把一部分变量限定为非基变量，得到限制主问题(Restricted Master Problem,RMP)。RMP的规模比MP小得多，这时候使用单纯形法在RMP上求最优解,But这个最优解只是RMP的最优解，不一定是MP的最优解，需要通过一个子问题(Subproblem)去检查那些未被考虑的变量中是否存在使RMP的Reduce Cost ＜ 0（忘了Reduce Cost是什么的同学，回到最优性判断一节复习）。如果有，那么把这个变量的相关系数加到RMP的系数矩阵A中，就多了一列，所以叫列生成！！！。重复上面的步骤，直至限制主问题RMP的Reduce Cost都大于等于0。

    用一个线性规划问题说明限定主问题RMP和子问题的关系(对！就是抄前面的那个LP)。

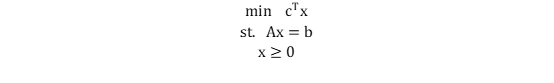
木材切割问题

    光说不练假把式,木材切割问题(Cutting Stock Problem)是学习列生成法绕不开的一个例子。假设有一定数量长度为20米的木材，需要长度为3、7、9、16米的木材各25、30、14、8根，怎样切割消耗的木材数量最少。

常规建模思路

列生成思路

把切割模式集合P全部枚举出来是困难的，几乎不可行，但是也没必要，不是每一种切割模式都会被用得到。

实验环节

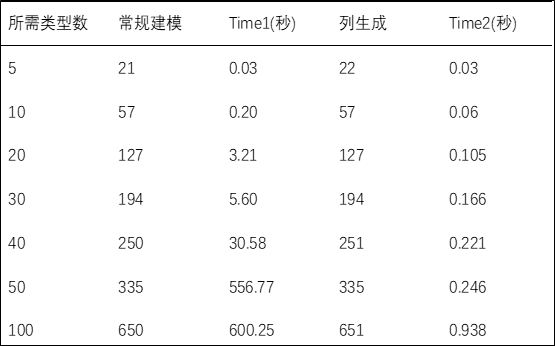
    写得我都麻了，开始进入实验环节，将两种建模方式都用Gurobi+Python写了个demo。列生成建模法参考了Gurobi官方的样例，常规建模自己写的，总得有一个是自己写的，免得你们说我不干活！在木材需求类型较少的情况下（10种以内），两种建模方式并没有很大的区别。但是从20种开始，需要的时间相差极大，列生成赢麻了！(其实100种木材，运行600秒时，常规建模法的gap还在2%左右，原则上不能说650是最优解！）

代码分析

1.常规建模法

第一步，生成需求的木材长度类型及其需要的数量，木材长度L=20(12-15）这种生成需求的方式，有一个漏洞，但是我已经写完了，不想改了，悟了请留言)

# -*-coding:utf-8 -*-
# @Time: 2022/6/9 21:38
# @Email: 151****3126@163.com
# @Author: Martin
import random
from gurobipy import *
random.seed(42)
# Types  = [3, 7, 9, 16]          # 需求长度
# Demand = [25, 30, 14,8]          # 需求的量
Types  = [] # 需求长度
Demand = [] # 需求的量
num = 100
for i in range(num):
    Types.append(random.randint(2,16))
    Demand.append(random.randint(9,20))
L = 20


K = 0  #设置一个20米长的木材数量上限
for i in range(len(Types)):
    K  += Demand[i]//(L//Types[i]) + 2
print(K)
x = {}
y = {}
m = Model("CSP_COMPACT")
for i in range(len(Types)):
    for k in range(K):
        name_x = "x_" + str(i) + "_" + str(k)
        x[i,k] = m.addVar(vtype= GRB.INTEGER,name=name_x)
for k in range(K):
    name_y = "y_" + str(k)
    y[k] = m.addVar(vtype=GRB.BINARY, name=name_y)


m.setObjective(quicksum(y[k] for k in range(K)),GRB.MINIMIZE)
#约束1
for i in range(len(Types)):
    m.addConstr(quicksum(x[i,k] for k in range(K)) >= Demand[i],\
    name = f"c1_i{i}")
#约束2
for k in range(K):
    m.addConstr(quicksum(Types[i]*x[i,k] \
    for i in range(len(Types)))<=L*y[k],name=f"c2_k{k}")
m.setParam(GRB.Param.TimeLimit,600)
m.optimize()
print(m.objval)

第二步，gurobi建模,第一种建模思路，直接按照gurobi的接口，一个一个循环写清楚就行，22-31行就添加了变量，别学我用这么低效的方法；33行在添加目标函数，并且设置了优化方向GRB.MINIMIZE最小化，循环加和请用quicksum() 真的YYDS；34-41添加约束1和2，对照着前面的常规建模看，其实是傻瓜式建模，42行设定最大运行时间600秒，万一解不出来，我可不想等一天！最后，优化运行，输出结果就好了。

2.列生成法建模

第一步是一样的。

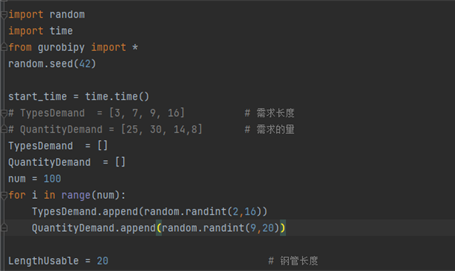
第二步，限制主问题-子问题迭代

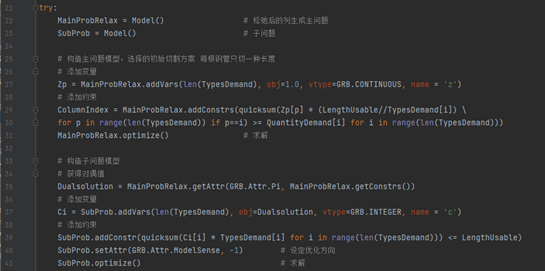
22行创建限制主问题，27行的addVars()会根据第一个参数，创建对应数量的变量，obj=1.0表示每个变量在目标函数中的系数是1.0，这种方式会自动写好目标函数，不需要像前面显式的再写一遍目标函数。29-30行添加和需求种类相同数量的切割模式(后面用例子说明)，不需要枚举所有切割模式。31求解限制主问题，33-41行，注释结合子问题模型看，很清楚，不说了。

案例说明

如下图所示，给出子集P1的初始切割模式，一共四种，和木材种类相同，列生成法的代码29-30行，限制主问题给出的切割模式就是这四种，变量松弛后获得右边的限制主问题，求解获得对偶变量的取值[0.166…,0.5,0.5,1.0]

代入子问题中，求解寻找新变量。

将新变量加入限制主问题中，继续迭代，得对偶变量值[0,0.5,0.5,1.0]。

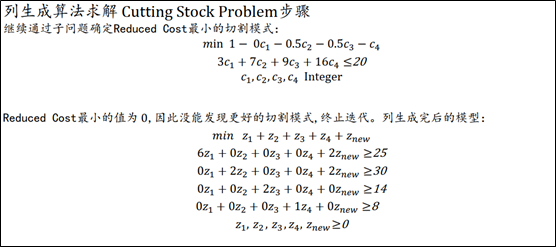
子问题再寻找新变量，但是Reduce Cost最小值为0了，停止列生成。

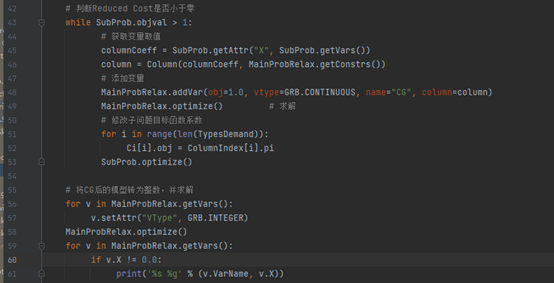
将下图中列生成结束后得到得模型的变量重新弄回整数约束，见列生成代码56-57行。

总结

    这篇分享诞生的背景是我最近在做关于branch-price-cut在cvrp问题应用的发展过程的一个文献调研作业，但是在这个问题上我还没写出代码，并且还涉及到各种Cuts，以及带资源约束的最短路问题等，太复杂了，做出来后，再逐步和大家分享。因为木材切割问题相对于其他更复杂的组合优化问题而言，还是比较简单的，就用它来做例子，当然用的各种cut和分支策略都是求解器默认的，并没有自己设计的cut和分支车略加进去，之后学废了再出一期。

        在私信框回复“column generation”,即可获得python源代码(不包含双引号“”哦）。