1. Prophet简介
Github:github.com/facebook/pro 官方网址:facebook.github.io/prop
2. Prophet算法原理

 表示趋势项,它表示时间序列在非周期上面的变化趋势;
表示趋势项,它表示时间序列在非周期上面的变化趋势; 表示周期项,或者称为季节项,一般来说是以周或者年为单位;
表示周期项,或者称为季节项,一般来说是以周或者年为单位; 表示节假日项,表示在当天是否存在节假日;
表示节假日项,表示在当天是否存在节假日; 表示误差项或者称为剩余项。Prophet 算法就是通过拟合这几项,然后最后把它们累加起来就得到了时间序列的预测值。
表示误差项或者称为剩余项。Prophet 算法就是通过拟合这几项,然后最后把它们累加起来就得到了时间序列的预测值。
趋势项模型
 如果增加一些参数的话,那么逻辑回归就可以改写成:
如果增加一些参数的话,那么逻辑回归就可以改写成: 这里的
这里的 分别为曲线的最大渐近值,曲线的增长率,曲线的中点。当
分别为曲线的最大渐近值,曲线的增长率,曲线的中点。当  时,恰好就是大家常见的 sigmoid 函数的形式。那么这里增加了参数的一般函数形式就为:
时,恰好就是大家常见的 sigmoid 函数的形式。那么这里增加了参数的一般函数形式就为:
 不可能都是常数,而很有可能是随着时间的迁移而变化的,因此,在 Prophet 里面,作者考虑把这三个参数全部换成了随着时间而变化的函数,也就是
不可能都是常数,而很有可能是随着时间的迁移而变化的,因此,在 Prophet 里面,作者考虑把这三个参数全部换成了随着时间而变化的函数,也就是 
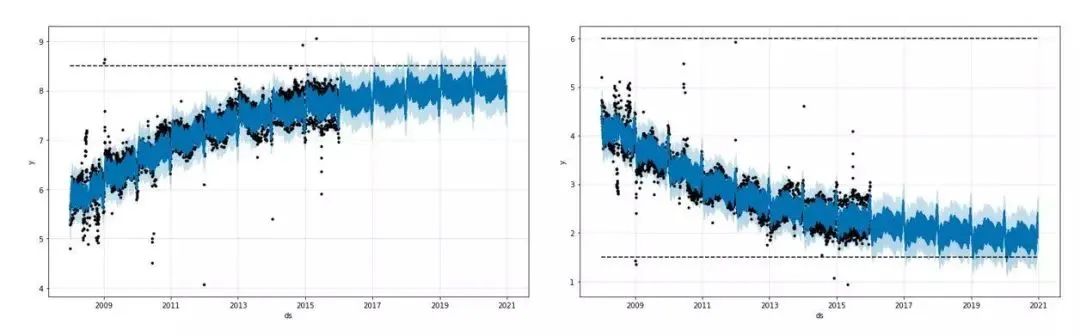
 ,这里的
,这里的 就是 change_point_scale。默认为0.05。因此总结起来就是变点的选择是基于时间序列的前 80% 的历史数据,然后通过等分的方法找到 25 个变点,而变点的增长率是满足 Laplace 分布
就是 change_point_scale。默认为0.05。因此总结起来就是变点的选择是基于时间序列的前 80% 的历史数据,然后通过等分的方法找到 25 个变点,而变点的增长率是满足 Laplace 分布  的。即这三个参数决定了k(t)和m(t)。两个函数的推导过程如下:
的。即这三个参数决定了k(t)和m(t)。两个函数的推导过程如下: 上。在这些时间戳上,增长率的变化changepoint_prior_scale,为向量
上。在这些时间戳上,增长率的变化changepoint_prior_scale,为向量  其中
其中  表示在时间戳
表示在时间戳  上的增长率的变化量,服从拉普拉斯分布。一开始的增长率使用
上的增长率的变化量,服从拉普拉斯分布。一开始的增长率使用  来代替,那么在时间戳
来代替,那么在时间戳  上的增长率就是
上的增长率就是  ,通过indicator函数
,通过indicator函数  表示为:
表示为:
 上面的增长率就是
上面的增长率就是  一旦变化量
一旦变化量  确定了,另外一个参数
确定了,另外一个参数  也要随之确定。在这里需要把线段的边界处理好,因此通过数学计算可以得到:
也要随之确定。在这里需要把线段的边界处理好,因此通过数学计算可以得到:
 中的常数换成关于时间的函数形式时
中的常数换成关于时间的函数形式时 就变成了分段的逻辑回归增长模型:
就变成了分段的逻辑回归增长模型:
 趋近于零的时候,
趋近于零的时候, 也是趋向于零的,此时的增长函数将变成全段的逻辑回归函数或者线性函数。
也是趋向于零的,此时的增长函数将变成全段的逻辑回归函数或者线性函数。季节项模型
周期性的变化因子是时间序列预测模型都会考虑的因素,为了拟合并预测季节的效果,Prophet基于傅里叶级数提出了一个灵活的模型。季节效应S(t)根据以下方程进行估算: 表示时间序列的周期,
表示时间序列的周期,  表示以年为周期,
表示以年为周期,  表示以周为周期。季节效应S(t)傅立叶级数形式是:
表示以周为周期。季节效应S(t)傅立叶级数形式是:

对季节性建模时,需要在给定N的情况下,估计参数 傅里叶阶数N是一个重要的参数,它用来定义模型中是否考虑高频变化。对时间序列来说,如果分析师认为高频变化的成分只是噪声,没必要在模型中考虑,可以把N设为较低的值。如果不是,N可以被设置为较高的值并用于提升预测精度。就作者的经验而言,对于以年为周期的序列
傅里叶阶数N是一个重要的参数,它用来定义模型中是否考虑高频变化。对时间序列来说,如果分析师认为高频变化的成分只是噪声,没必要在模型中考虑,可以把N设为较低的值。如果不是,N可以被设置为较高的值并用于提升预测精度。就作者的经验而言,对于以年为周期的序列 而言,
而言, ;对于以周为周期的序列
;对于以周为周期的序列 而言,
而言, 。
。
当  时,
时,

当  时,
时,

因此,时间序列的季节项就是:  而
而  。这里的
。这里的  值越大,表示季节的效应越明显;这个值越小,表示季节的效应越不明显。同时,在代码里面,seasonality_mode 也对应着两种模式,分别是加法和乘法,默认是加法的形式。
值越大,表示季节的效应越明显;这个值越小,表示季节的效应越不明显。同时,在代码里面,seasonality_mode 也对应着两种模式,分别是加法和乘法,默认是加法的形式。
节假日项模型
现实生活中的预测场景中有很多节假日,而且不同的国家有着不同的假期。还有类似于618、双十一等这样不列入官方节日,但是对于指标预测影响非常重要的日期。在 Prophet 里面,通过维基百科里面对各个国家的节假日的描述,hdays.py 收集了各个国家的特殊节假日。Prophet还允许分析师使用过去和未来事件的自定义列表,例如印度的The Super Bowl,国内的双十一等。
由于每个节假日对时间序列的影响程度不一样,例如春节,国庆节则是七天的假期,对于劳动节等假期来说则假日较短。因此,不同的节假日可以看成相互独立的模型,并且可以为不同的节假日设置不同的前后窗口值,表示该节假日会影响前后一段时间的时间序列。用数学语言来说,对与第  个节假日来说,
个节假日来说,  表示该节假日的前后一段时间。为了表示节假日效应,我们需要一个相应的indicator函数,同时需要一个参数
表示该节假日的前后一段时间。为了表示节假日效应,我们需要一个相应的indicator函数,同时需要一个参数  来表示节假日的影响范围。假设我们有
来表示节假日的影响范围。假设我们有  个节假日,那么
个节假日,那么

其中
其中  该正态分布的标准差默认值是 10,当值越大时,表示节假日对模型的影响越大;当值越小时,表示节假日对模型的效果越小。用户可以根据自己的情况自行调整。
该正态分布的标准差默认值是 10,当值越大时,表示节假日对模型的影响越大;当值越小时,表示节假日对模型的效果越小。用户可以根据自己的情况自行调整。
模型拟合
结合上面对增长项,季节项,节假日项三方面的详细讲解,现在可以用线性将三块结合一起来拟合时间序列:

在 Prophet 中,可以使用 Prophet 默认的参数,也可以自己设置以下四种参数:
Capacity:在增量函数是逻辑回归函数的时候,需要设置的容量值。
Change Points:可以通过 n_changepoints 和 changepoint_range 来进行等距的变点设置,也可以通过人工设置的方式来指定时间序列的变点。
季节性和节假日:可以根据实际的业务需求来指定相应的节假日。
光滑参数:
 changepoint_prior_scale 可以用来控制趋势的灵活度,
changepoint_prior_scale 可以用来控制趋势的灵活度,  seasonality_prior_scale 用来控制季节项的灵活度,
seasonality_prior_scale 用来控制季节项的灵活度,  holidays prior scale 用来控制节假日的灵活度。
holidays prior scale 用来控制节假日的灵活度。
1. 趋势参数
参数 | 描述 |
growth | ‘linear’或‘logistic’规定线性或逻辑趋势 |
changepoints | 包括潜在突变点的日期列表(默认为自动识别) |
n_changepoints | 若不指定突变点,需要提供自动识别的突变点数 |
changepoint_prior_scale | 设定自动突变点选择的灵活性 |
参数 | 描述 |
yearly_seasonality | 周期为年的季节性 |
weekly_seasonality | 周期为周的季节性 |
daily_seasonality | 周期为日的季节性 |
holidays | 内置的节假日名称和日期 |
seasonality_prior_scale | 改变季节模型的强度 |
holiday_prior_scale | 改变假日模型的强度 |
3. Prophet实战(附Python代码)
数据链接:https://datahack.analyticsvidhya.com/contest/practice-problem-time-series-2/
#import dataimport pandas as pdimport numpy as npfrom fbprophet import Prophet#Read train and testtrain = pd.read_csv('Train_SU63ISt.csv')test = pd.read_csv('Test_0qrQsBZ.csv')#Convert to datetime formattrain['Datetime'] = pd.to_datetime(train.Datetime,format='%d-%m-%Y %H:%M')test['Datetime'] = pd.to_datetime(test.Datetime,format='%d-%m-%Y %H:%M')train['hour'] = train.Datetime.dt.hour
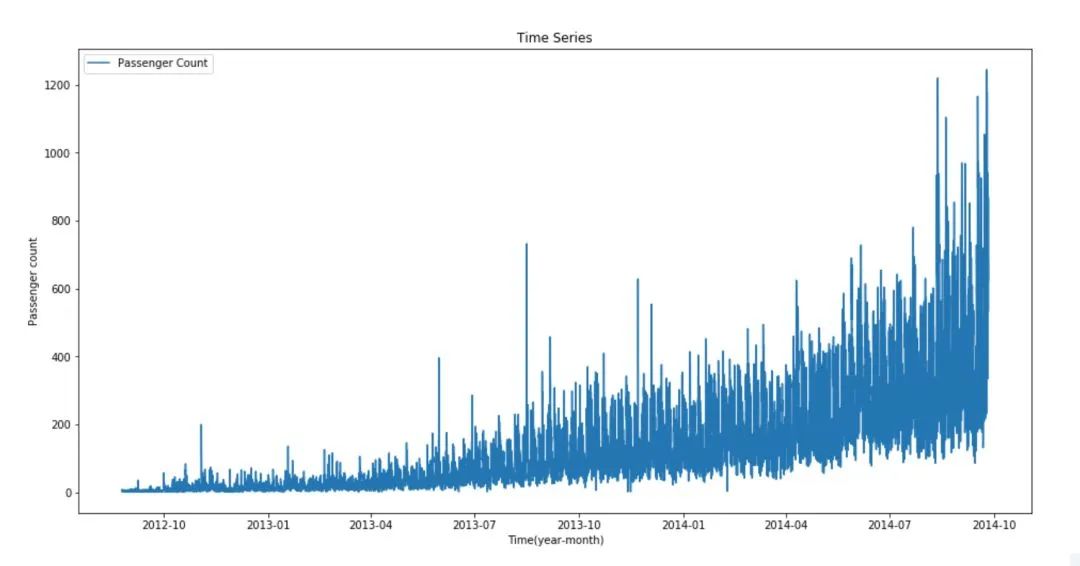
我们可以看到时间序列中有很多噪声。我们可以对其进行重采样并汇总,得到一个噪声更少的新序列,进而更易建模。
# Calculate average hourly fractionhourly_frac = train.groupby(['hour']).mean()/np.sum(train.groupby(['hour']).mean())hourly_frac.drop(['ID'], axis = 1, inplace = True)hourly_frac.columns = ['fraction']# convert to time series from dataframetrain.index = train.Datetimetrain.drop(['ID','hour','Datetime'], axis = 1, inplace = True)daily_train = train.resample('D').sum()
Prophet要求时间序列中的变量名为:
y -> 目标(Target)
ds -> 时间(Datetime)
因此,下一步是基于上述规范来转换数据文件:
daily_train['ds'] = daily_train.indexdaily_train['y'] = daily_train.Countdaily_train.drop(['Count'],axis = 1, inplace = True)
拟合Prophet模型(未设置的参数表明默认原设置):
#参数设置m = Prophet(yearly_seasonality = True, seasonality_prior_scale=0.1)#模型拟合m.fit(daily_train)#预测窗口future = m.make_future_dataframe(periods=213)#模型预测forecast = m.predict(future)#预测结果可视化fig = m.plot(forecast)
我们可以通过以下命令来查看各个成分:
m.plot_components(forecast)
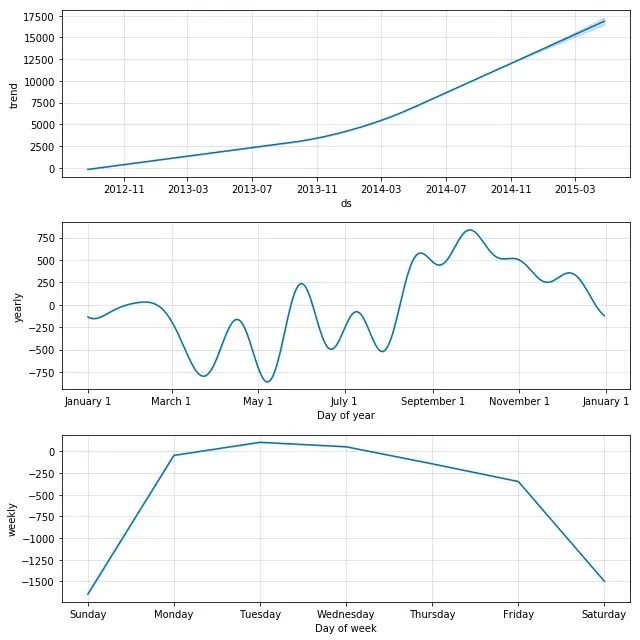
基于每日数据的预测如下。









