点击上方蓝色【数据攻略】关注+星标~
第一时间获取最新内容

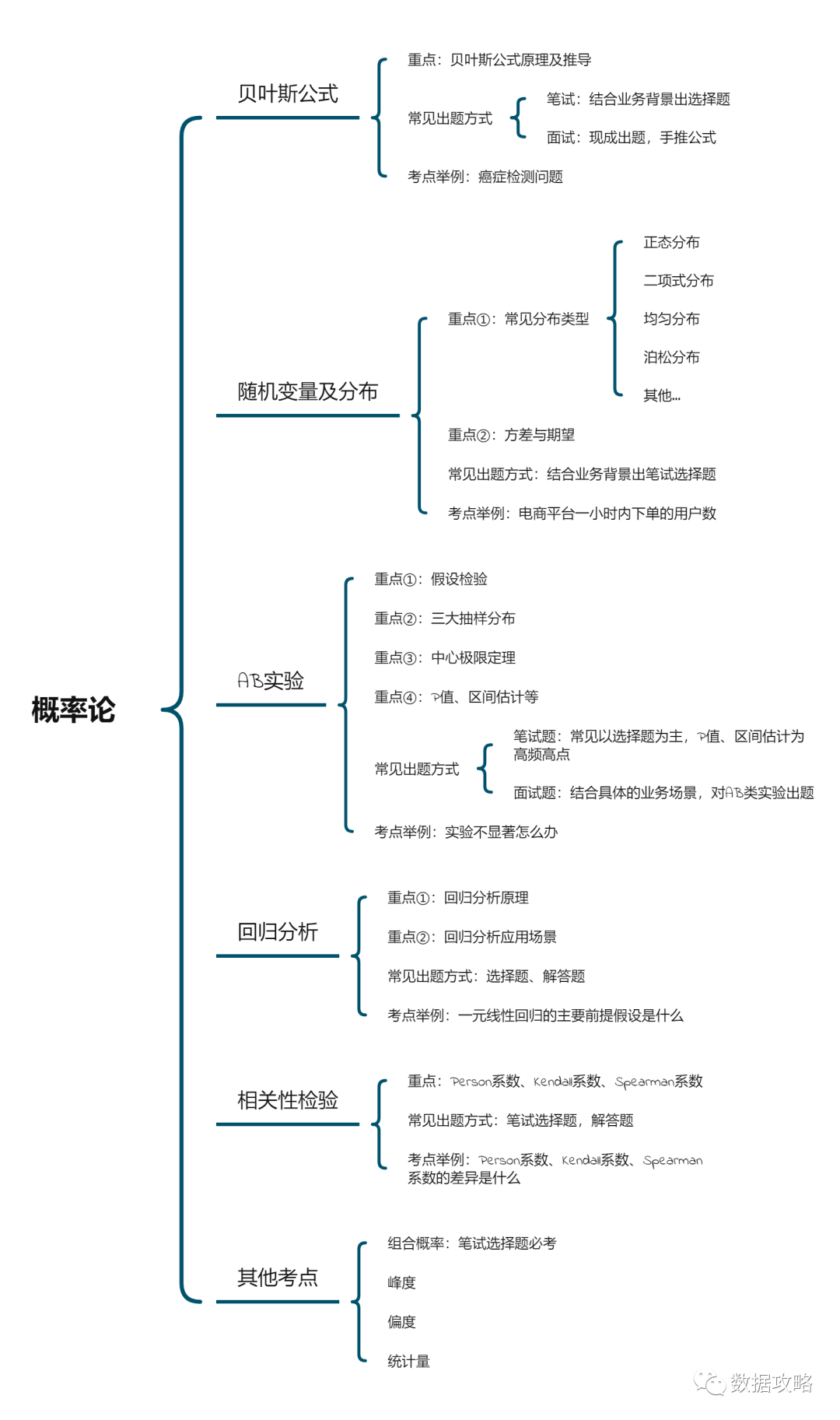

一、原理推导
二、样例解析
三、笔试真题
我们先用大白话理解一番:
之所以有概率一说,是因为我们对还没发生的事情(B)拿捏不准
但好在有时能有参考信息(条件Ai),所以咱就把这参考信息的每种情况都罗列出来,再来计算当每个参考信息发生时B这事发生的概率,综合汇总后就是这件事(B)发生的概率。
这就是所谓的全概率计算思想——直接求B有时候实在太难了,那咱就分而治之,逐个击破,达到目的!
贝叶斯其实要解决的问题,和全概率相反:

理解注意:Ai和B事件发生是有先后关系的,先A后B,有所谓的条件概率思想在里面,也是理解全概率和贝叶斯的基石所在。
▌符号定义
① P(A) : 事件A发生的概率
② P(B):事件B发生的概率
③ P(AB):事件A和事件B同时发生的概率
④ P(A|B):已知事件B发生,事件A发生的概率
⑤ P(B|A):已知事件A发生,事件B发生的概率
▌全概率公式
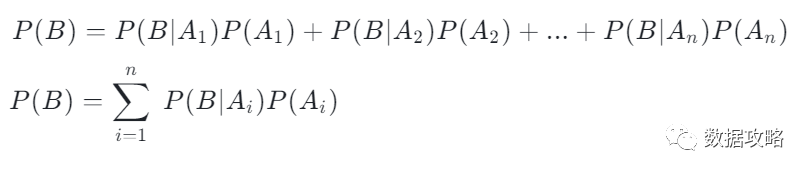
由条件概率公式可知:
P(AB)=P(A|B)P(B)=P(B|A)P(A)
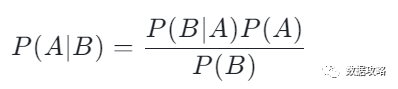
▼如果A事件拢共就两种情况
由全概率公式可得:
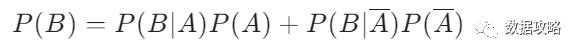
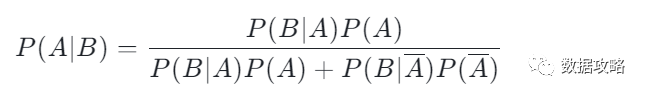
▼如果A事件有多种情况,那么分母代入 即可
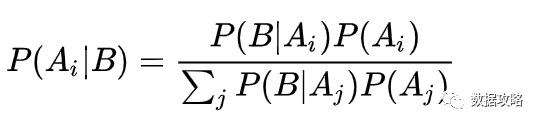
为方便大家理解,引入新冠疫情的例子
▌定义
① 事件A的定义:得了新冠。
② 事件B的定义:检测为阳性。
③ P(A|B)为:已知检测为阳性,得新冠的概率。
④ P(B|A)为:已知得了新冠,检测为阳性的概率。
假设检测的准确性是99%,也就是
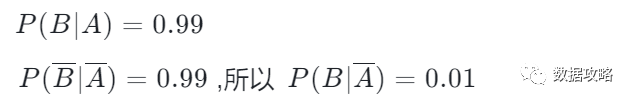
P(A)=0.0001,得新冠为万分之一的概率
▌问题
假设今日张三做核酸检测结果为阳性
请问张三得新冠的概率是多少?
▌解答
由贝叶斯公式可得

也就是说,张三检测为阳性,得新冠的概率为1%.
假设此刻你到清华大学,作为学霸府邸
如果清华大学同学IQ值大于110的概率为0.9999
那么此时有个同学有一道简单高等数学题做不出来
如果让你去判断该同学的IQ值是否低于110
你给出的结果很有可能是,否
也就是这位同学依旧是高智商
理由是:
基于高智商的认知
即便现在得到的结果是相反的
但依旧有很大可能是高智商
这就是贝叶斯
▌笔试真题1
「网易」现在有一个程序由A,B两个同学结对编程完成,在整个程序中的代码比例是3:5,据往常的统计A同学的千行代码缺陷率为0.1% ,B同学的千行代码缺陷率为0.15% ,现在在改程序中发现了一个缺陷,那么是由A同学的代码引起的缺陷的概率为( )
A 28.6%
B 37.5%
C 40.0%
D 47.4%
事件A:A同学编写代码,P(A)=3/8
事件B:B同学编写代码,P(B)=5/8
事件C:BUG事件
P(C|A)=0.1%
P(C|B)=0.15%
P(A|C)=P(A)P(C|A) (P(A)P(C|A)+P(B)P(C|B))
P(A|C)=(3/8*0.1%) (3/8*0.1%+5/8*0.15%)
P(A|C)=28.6%
★解题思路2:
假设A写了3000行,B写了5000行
那么A写了30个bug,B写了75个
发现1个bug,是A写的概率是30/(30+75)=28.6%
▌笔试真题2
「搜狐」所有人口中,某癌症的患病率为0.008。对有癌症的病人,医院的化验测试有2%的可能错判其无癌症。对无癌症的病人,有3%的可能错判其有癌症。问:现有一新病人,化验测试表明其有癌症,该病人实际患有癌症的概率是多少?(计算过程四舍五入保留4位小数)( )
A 0.0078
B 0.0298
C 0.2085
D 0.9800
正确答案:C
★解题思路:
事件A1:患有癌症,P(A1)=0.008
事件A0:没有癌症,P(A0)=0.992
事件B1:检测出患有癌症,P(B1 | A0)=0.03
事件B0:检测没有癌症,P(B0 | A1)=0.02
所以 P(B1 | A1)=0.98
P(A1 | B1) = P(B1|A1)*P(A1)
[P(B1|A1)*P(A1)+P(B1|A0) ]
P(A1|B1)=(0.98*0.008)/[0.98*0.008+0.03*0.992]
P(A1|B1) =0.2085
「阿里巴巴」假设淘宝用户上的用户看到一个商品后购买的概率是5%,收藏的概率是20%,而用户收藏一个商品之后购买的概率是20%,那么已知某用户看到某商品之后完成了购买,那么该用户收藏过该商品的概率是( )。
A 60%
B 70%
C 80%
D 90%
正确答案:C
★解题思路:
事件A1:购买,P(A1)=5%
事件A0:未购买,P(A0)=95%
事件B1:收藏商品,P(B1)=20%
事件B0:未收藏商品,P(B0)=80%
P(A1 | B1) = 20%
P(B1 | A1) = P(A1,B1)/P(A1)
P(B1 | A1) =P(A1 | B1)*P(B1) P(A1)
P(B1 | A1) = 20%*20% 5% = 80%
「360公司」考虑两队之间的足球比赛:队0 和队1。假设65%的比赛队0胜出、P(Y=0)=0.65。剩余的比赛队1胜出、P(Y=1)=0.35。队0获胜的比赛中只有30%在队1的主场、P(X=1|Y=0)=0.3,而队1获胜的比赛中75%是主场获胜、P(X=1|Y=1)=0.75。则队1在主场获胜的概率即P(Y=1|X=1)为:
A 0.57
B 0.42
C 0.69
D 0.28
正确答案:A
★解题思路:
事件Y0:0队获胜,P(Y0)=65%
事件Y1:1队获胜,P(Y1)=35%
事件X0:0队主场
事件X1:1队主场
P(X1 | Y0)=30%,P(X1 | Y1)=75%
P(X1)=P(X1 | Y0)P(Y0)+P(X1 | Y1)P(Y=1)
P(X1)=0.4575
P(Y1 | X1)=P(X1 | Y1)*P(Y1)/P(X1)=0.57
「携程」假设箱子中苹果和梨子的数量比是2:1,储存期间苹果腐烂的概率是0.02,梨子腐烂的概率是0.01。现在有一水果腐烂,求该水果是苹果的概率()
A 0.80
B 0.75
C 0.67
D 0.33
正确答案:A
★解题思路:
P(苹果)=2/3
P(梨)=1/3
P(腐烂 | 苹果) = 0.02
P(腐烂 | 梨) = 0.01
P(苹果 | 腐烂) = P(苹果)*P(腐烂 | 苹果)
/ ( P(苹果)P(腐烂 | 苹果) + P(梨)P(腐烂 | 梨))
P(苹果 | 腐烂) =0.8
如若盼 追更 『求职类』干货系列 

 往期好文推荐
往期好文推荐 
更多 『求职干货』 & 『日常学习』 系列好文,等你发现~

Ps. 微信推文改了规则
看完记得设置为 “ 星标 ”
不然我会消失的