『网易提前批』大厂笔试真题系列（二）

数据攻略 2022-07-13

365

点击上方蓝色【数据攻略】关注+星标~

第一时间获取最新内容

大家好，我是六哥~

最近一些厂的提前批已陆续开始了

（Ps：需要靠谱内推码的同学，可以后台联系我

）

前几篇已对笔面试各种题型做了系统梳理

但俗话说：百看不如一练

因此，前面给大家梳理了携程数据分析笔试真题

【数据分析岗】大厂笔试真题系列（一）

本篇继续为大家输出笔试真题此系列第二篇

『网易提前批』数据分析笔试题

文内含答案，可作为参考

我希望你，掐好时间，模拟自测

------正文手动分割线------

本文结构速览：

一、选择题

二、编程题

一、选择题

[1] 在5张卡片上按顺序写上laval这五个字母，并依次放入5个盒中，有人从中任意取出两张卡片使用，但是在放回时，忘记了两张卡片各自的位置，求此人将卡片随意放回两个空盒子后卡片顺序仍为laval的概率 ( )

A、 2/5

B、 1/2

C、 1/5

D、 3/5

答案：D

[2] 有一堆石子，共80颗，甲，乙轮流从该堆中取石子，每次可以取2,4或者6颗，取得最后的石子的玩家为赢家，甲乙都足够聪明都想赢，若甲先取，则（）

A、其他说法都不正确

B、甲乙都是50%几率获胜

C、甲必胜

D、乙必胜

答案：D

[3] x+y+z+m=10，其中x,y,z,m都是正整数，那么x,y,z,m有多少种不同的取值组合（）

A、 84

B、 112

C、 165

D、 220

E、 64

答案：A

[4] 若总体X～N(µ,δ^2),其中δ^2已知，当样本容量保持不变时，如果置信度减小，则的置信区间（）.

A、长度变大

B、都有可能

C、长度变小

D、长度不变

答案：D

[5] 访问记录visit表中包含日期date,用户user_id,访问的页面url 3个字段，以下哪个选项不能计算'2019-03-11'这一天访问过页面的所有用户数（）

A 、

SELECT count(DISTINCT user_id) 
FROM visit 
WHERE date = '2019-03-11'

B、

SELECT count(user_id) 
FROM visit 
WHERE date = '2019-03-11' 
GROUP BY date

C、

SELECT COUNT(user_id)
FROM 
(
  SELECT user_id 
  FROM visit 
  WHERE date = '2019-03-11' 
  GROUP BY user_id
 ) f

D、

SELECT COUNT(user_id)
FROM 
(
  SELECT DISTINCT user_id 
  FROM visit 
  WHERE date = '2019-03-11'
) f

答案：B

[6] 设随机变量X和Y都服从正态分布,且它们不相关，则（）

A、 X + Y服从一维正态分布

B、 (X, Y)服从二维正态分布

C、 X与Y未必独立

D、 X与Y一定独立

答案：C

[7] 小明在玩掷骰子的游戏，将一颗骰子掷了两次，两次骰子的点数之和为7，求其中一次掷到6点的概率 ( )

A、 1/12

B、 1/3

C、 1/18

D、 1/6

答案：B

[8] 一个盒子中有三个大小相同的球，这三个球可能是红和蓝两种颜色，并且一个球是红的还是蓝的是等可能的。已知其中有一个是红色的，那么至少有一个球是蓝色的概率是多少（）

A、 3/4

B、 7/8

C、 1/3

D、 6/7

答案：D

[9] 以下不是稳定的排序算法的是（）

A、插入排序

B、归并排序

C、冒泡排序

D、快速排序

答案：D

[10] 设随机变量X和Y的相关系数为0.5，E(X) = E(Y) = 0, E(X^2) = E(Y^2) = 2, 则E[(X +Y)^2] = ( ).

A、 2

B、 8

C、 6

D、 4

答案：C

[11] 某电灯泡生产商声称，它们生产的电灯泡的平均使用时间为85小时。质检部门抽取20个电灯泡的随机样本，在的显著性水平下，检验结果是未能拒绝原假设，这意味着()

A、该企业生产的电灯泡的平均使用时间是85小时

B、没有证据证明该企业生产的电灯泡的平均使用时间不是85小时

C、没有证据证明该企业生产的电灯泡的平均使用时间是85小时

D、该企业生产的电灯泡的平均使用时间不是85小时

答案：B

[12] 在10件产品中有五件是残次品，从中任取五件，求其中至少有两件是残次品的概率( )

A、 113/126

B、 4/5

C、 105/126

D、 1/12

答案：A

[13] 如下哪些sql语句能查询出每门课都都大于80分的学生姓名,部分数据如下表(student_score)所示：

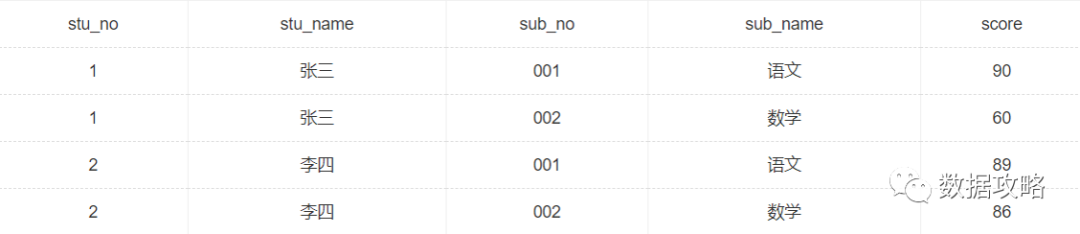
A、

select distinct stu_name 
from student_score 
where stu_name not in 
  (select distinct stu_name 
   from student_score 
  where score <= 80)

B、

select stu_name 
from student_score 
group by sub_name 
having min(score) >80

C、

select distinct stu_name 
from student_score 
where score >80

D、

select stu_name 
from student_score 
group by stu_name having min(score) >80

答案：A

[14] 有无限多水源，一个4L无刻度桶和一个9L无刻度桶，只利用这2个无刻度桶，将不可能获得（）L水

A、 8

B、 1

C、 7

D、 11

E、 3

F、所有选项均能获得

答案：F

[15] 以下是泊松分布概率密度函数的是（）

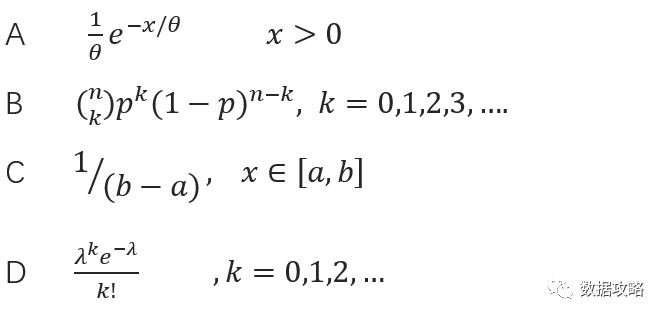
答案：D

二、编程题

▌题目一：

▼ 题目描述：

小易有一个初始为空的数字集合，支持两种操作：1、加入数字x到集合中。

2、询问集合中是否存在一个子集，满足子集中所有数字的Or值恰好为k。

Or为二进制按位或操作，C++中表示为"|"。小易希望你能解决这个问题。

▼ 输入：

第一行数字q,表示操作个数接下来q行，每行两个数字：1 x表示插入数字x

2 x表示询问数字x(即题设中询问的数值k)

1<=q<=100000,1<=x<=100000

▼ 输出：

对于每个询问，输出"YES"或者"NO"表示是否存在。

▼ 样例输入：

9 1 4 2 5 1 9 1 15 2 4 1 11 2 10 2 7 2 9

▼ 样例输出：

NO YES NO NO YES

▼ 答案（Python）

import sys
def main():
    def exist(x):
        y = 0
        for i in lst:
            if i | x == x:
                y |= i
                if x == y:
                    return True
        else:
            return False


    lst = set()
    res = []
    q = int(sys.stdin.readline().strip())
    m = map(int, sys.stdin.read().split())
    xlst = list(zip(m, m))
    for i, j in xlst:
        if i == 1:
            lst.add(j)
        else:
            res += ['YES' if exist(j) else 'NO']
    print(*res, sep='\n')


if __name__ == '__main__':
    main()

▌题目二：

▼ 题目描述：

小易给定了一个长度为n的数字序列，对于每一个1<=k<=n，小易希望能求解出所有长度为k的连续子序列的最大值中的最小值。

▼ 输入：

第一行数字n

接下来一行是一个长度为n的数字序列

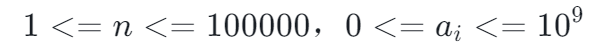
▼ 输出：

一行n个数字，第i个数字表示k = i时的答案。

▼ 样例输入：

6 1 3 2 4 6 5

▼ 样例输出：

1 3 3 4 6 6

▼ 答案(C++)：

#include <map>
#include <vector>
#include <stdlib.h>
#include <stdio.h>


using namespace std;
int main() {
    int n, i, temp, left, right;
    scanf("%d", &n);
    vector<int> a;
    map<int, int> radius;
    map<int, int>::iterator key;
    for (i = 0; i < n; ++i) {
        scanf("%d", &temp);
        a.push_back(temp);
    }
    for (i = 0; i < n; ++i) {
        left = i - 1;
        right = i + 1;
        while (left > -1) {
            if (a[left] > a[i]) {
                break;
            }
            --left;
        }
        while (right < n) {
            if (a[right] > a[i]) {
                break;
            }
            ++right;
        }
        int sum = right - left - 1;
        key = radius.find(sum);
        if (key == radius.end()) {
            radius[sum] = a[i];
        } else {
            if (radius[sum] > a[i]) radius[sum] = a[i];
        }
    }
    int min = radius[n];
    map<int, int>::reverse_iterator rkey;
    for (rkey = radius.rbegin(); rkey != radius.rend(); rkey++) {
        if (min < rkey->second) {
            rkey->second = min;
        } else {
            min = rkey->second;
        }
    }
    int rRes = 1;
    for (i = 1; i <= n; ++i) {
        key = radius.find(rRes);
        if (key == radius.end()) {
            while (key==radius.end()) {
                ++rRes;
                key = radius.find(rRes);
            }
            printf("%d ", key->second);
        } else {
            printf("%d ", key->second);
            if (rRes == i) {
                ++rRes;
            }
        }
    }
    return 0;
}