【数据分析岗】概率论类高频考点框架这篇，重点讲解【概率论】系列 之 假设检验 常见高频考点 ↓
涉及考点：假设检验、统计功效、最小样本量
内含 推导 及 考点解析
也是AB实验中非常常用的两个基本概念
因此，是各大厂面试官考察应聘者对假设检验的 真实 掌握情况
考点举例：
▶ 第一类错误的定义？
▶ 统计功效的定义，以及应用场景？
▶ 统计功效较低的影响是什么？
假设检验
假设检验作为AB实验最基础的知识点。
我们必须熟记第一类错误和第二类错误的定义，以及检验统计量相关的前提条件。
（关于检验统计量后面我们将开展详细的文章讲解，在此不进行阐述）
原假设，用H0表示，通常将不应轻易加以否定的假设作为原假设。
备择假设，用H1表示，当H0被拒绝时而接收的假设。
H0为真但由于随机性使样本观测值落在了拒绝域中，从而拒绝原假设H0，这种错误称为第一类错误，也称为α错误。 H0不为真，但由于随机性使样本观测值落入接受域中，从而接受假设H0，这种错误称为第二类错误，也称为β错误。
下面用一张图来理解一下这两类错误：
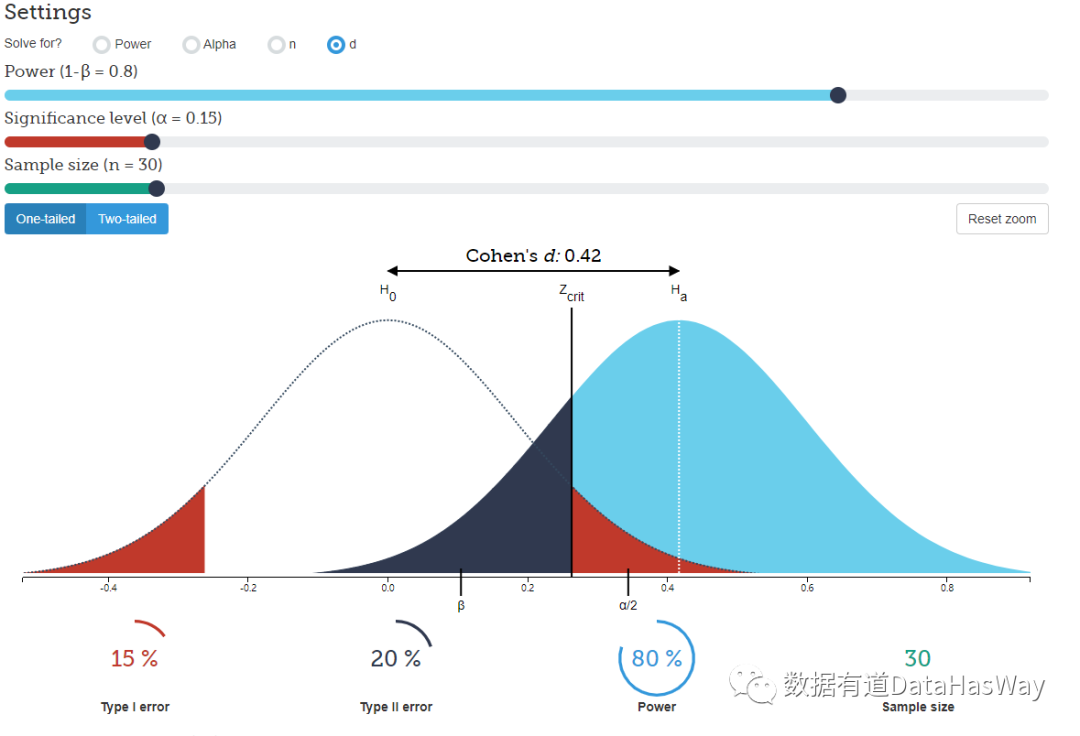
互联网每日可获取大量的用户行为数据，根据统计量的检验方法，当样本量较大的时候，我们采用U（正态分布）检验法。
后面我们也将基于U检验法进行相关的讲解和推导。
统计功效
统计功效（statistical power）是指，当H0为假拒绝H0的概率。也就是1-β的概率。
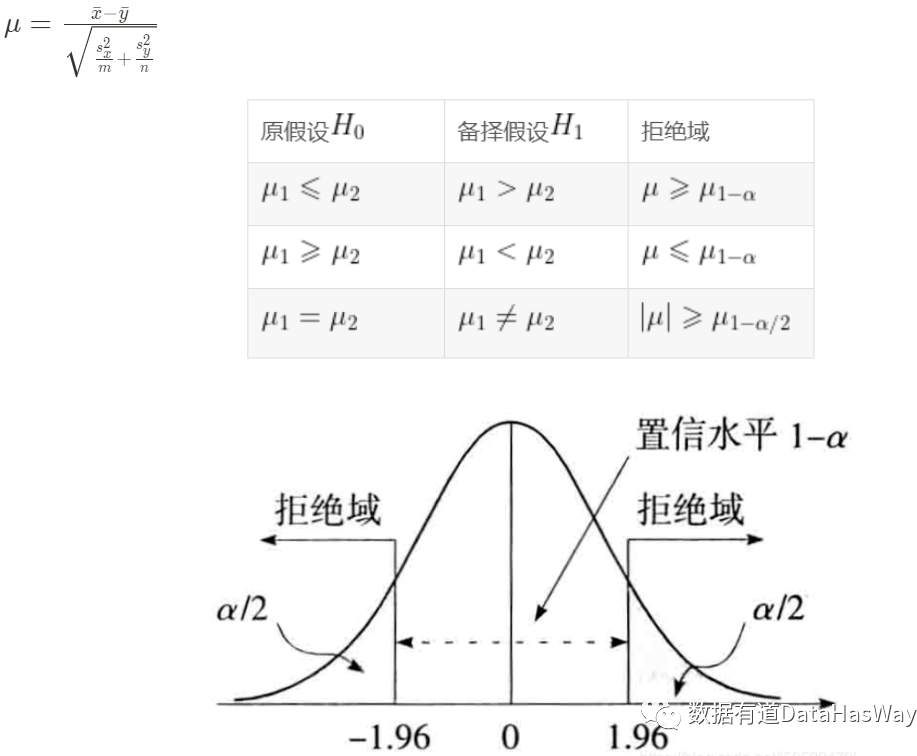
下面我们以双边检验为例，单边检验只要进行相应的替换即可。
原假设和备择假设如下：
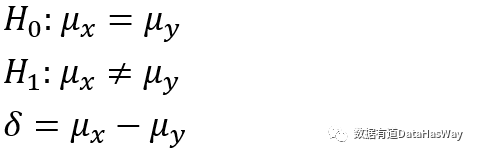
假根据第二类错误的定义当H0为假时，接受H0的概率，下面来详细推导统计功效的计算逻辑。
对于单边检验，功效power的推导结果为：
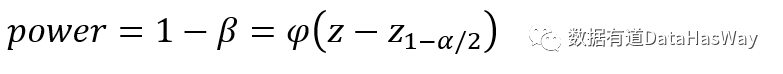
▼ 划重点：
统计功效的定义及公式展示结果。
统计功效低，那么当AB两组差异真的存在时，我们很可能会错误判断两组差异不存在。
我们一般把统计功效定义在80%（或90%）以上，即β在0.2（或0.1）以下。认为这样的可信度是可以接受的。
最小样本量
最小样本量是在准备开展AB实验时，对目标提升效果预计需要的样本量估算，方便提前估算出AB实验的运行周期。
以单边检验为列，进行最小样本量计算，假设两组样本数量相等，均为n ，则最小样本量为：
双边检验的推导类似，最小样本量为：
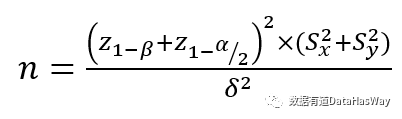
▼ 划重点：最小样本量同时考虑了第一类、第二类错误。
以上，就是关于假设检验 | 统计功效 | 最小样本量的考点梳理。
如若其中某一方面、某一细节点对你有帮助，欢迎点赞，点亮在看
也可以在公众号后台找到我，说说你目前的困惑 ~
欢迎关注
更多 『求职干货』 & 『日常学习』 系列好文，等你发现~
