朝阳目标上有这样一道题:
大球A原来所带的电荷量为Q,小球B原来不带电。现在让小球与大球接触,达到静电平衡时,小球获得的电荷量为q。现给A球补充电荷,使其所带电荷量为Q,再次让小球接触大球,每次都给大球补充到电荷量为Q。问:经过反复多次接触后,小球所带的电荷量为多少?
常理看这个题似乎不难,但是它不容易真让学生懂。我们都知道,“懂”比“会”要难太多了。学生知道怎么模仿,但不知道为什么要这样做。
有小伙伴给我发来网页上的截图,网页上面的解法,核心关键是一语没道破两球带电量总要成比例,但却一直在依据成比例列式子!
下面就记录一下给小伙伴答疑时的、我的表述方式。好像好懂一点儿。
一、深刻理解“带电量”的意思
静电场一章一开始就说了物体带电的意思,所谓“带”,意思是“持有”。就是不带电的物体,跟别人接触一下,它“抢夺”别人的电荷的能力与别人“保护”自己的电荷不被夺走会达到一种平衡,当带电达到稳定状态,想抢夺的再抢夺不走别人所拥有、想保护的再保护不了自己所失去。
这就好理解了。不论原来他人有多少,带电量之“带”,是一方之“夺”与另一方之“护”的能力之象征,故此两球带电量必成比例。
如果抛开“比例”这个词不提它。列个表、再加个代换思想(数学基本功吧?)也容易。
第1次分配后:Q-q、q;
第2次分配后:Q+q-q1、q1;
假设数不清的某一次分配后,A球带电恰好是第2次分配后的k倍,k只是一个实数。比如k=5吧,那就好像是有5个人在一起做了A、B接触再分开看B球带电多少这件事。然后这5个人又把5个A球(像空心皮球那样)套在一起观察、5个B球一起观察,看它们作为帮派你抢我夺的能怎么着?那显然可以断定B球们带电是kq1这么多。如果k=5.1、k=5.10001……结论都一致。因为这个过程中,A还是那个A、B还是那个B,“夺”与“护”的能力没变。
直接看最后一次吧。最后A上有Q,无非就是先前带电的k倍,于是B球带电也是先前带电的k倍。先前是哪个先前?第1次分配,于是可以列式。(图中标注正负号混了)
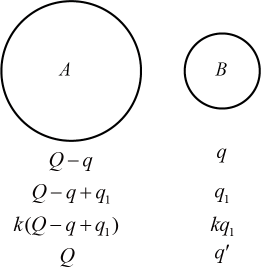
二、适当建构模型
高中静电场教材里还有什么地方能定量地研究和计算电量这件事呢?装电的容器,电容器。
考虑到电荷们被抢夺完毕时,A、B间接触与不接触,也就是弄根导线把A、B连接或不连接,不影响电荷的分配。类比到地面上的高度,两个瓶口一样高度了,A瓶口对着B瓶口倒水,谁也再倒不出、谁也再装不下,等高了;也就这里的A、B两个球等势了。假设在无穷远还有两个金属极,并且A、B带了正电荷。就可以设A、B电势均为φ。A与无穷远的极构成电容器C1、B与无穷远的极构成电容器C2。
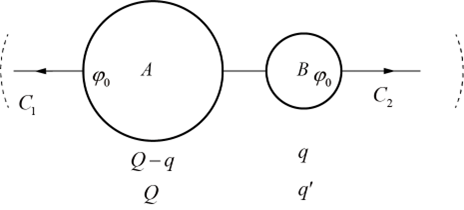
由图,设A最后被充满Q电量时,电势变成φ1了,于是Q-q=C1φ0、Q=C1φ1,q=C2φ0、q'=C2φ1。可解。
三、遗留的没太大意义但有趣的问题
有的小伙伴被引入到“不完全归纳法”的坑儿里去了,类似于数列求通项。大体思路是看电荷分配,如表格:
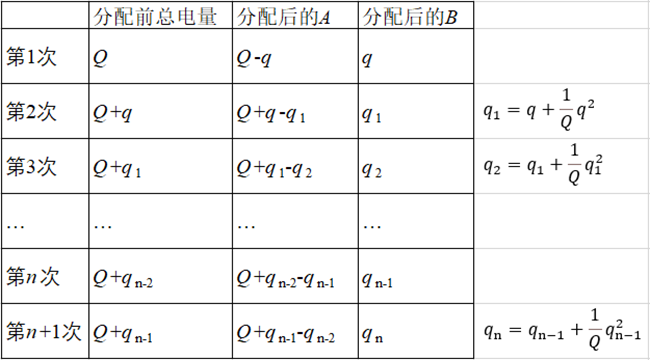
这样,我们如果能够得到qn的通项,令其通项中相邻的两项相等,则可解出项数n,这个n的意思,就是对应这样的操作:A、B两球在那碰啊碰啊碰,但是电荷不再重新分配了,而此时从表格最后一行第3列上可以看到,A上的电量就是Q。
于是问题聚焦在如何求出形如an=an-1+Kan-12的通项{an}。我原来的想法是构造一个带着cosx、ex的函数,比如双曲余弦函数,平方之后还能落回到原函数形式,没解决;再后来请教了N多地面上的、网络上的数学老师们,没解决;再再后来在一些专业点儿的数学论坛和博客上看到:这种邻项平方形的数列,只有极为苛刻的K值,才可能有解析解!包括所谓不动点法求通项,也不是都能解决通项的。
但是反过来细细推究起来,其实以上面的“相邻的两项相等”作为A球带电的终极状态,显然是头脑一热掉入的第二个坑儿:就算我们去求qn的极限,应该也求不出什么来,因为n趋于无穷时,qn趋于零,qn/qn-1是零比零型极限,好像又是走不通呢。
果然是一条没有困难创造困难也要上的道路。






