1 背景

在日常生活中，我们常需要从大量数据中筛选出符合某些空间约束的数据，比如在出行时，我们可能想要找到附近500m内的共享单车。解决这样的问题的一个简单想法是从数据库中取出所有共享单车的记录，然后根据用户的位置与共享单车的位置得到用户与各个共享单车的距离，最后再筛选出距离小于500m的数据。然而，这个算法显然是十分耗时的。

在数据库中一般可以利用索引来进行查询的优化。比如传统的MySQL使用B树或B+树作为索引来加速查询。然而，建立B树或B+树的前提是数据是可以排序的，空间信息作为二维的数据，并不能直接进行排序，所以想为空间信息添加索引是比较困难的。接下来本文将介绍一些比较常用的空间索引。

2 R树

如图 1和图 2所示，D1是带有空间信息的数据，R8就是D1的MBR。R树最左边的叶子节点存储了D1、D2、D3所对应的MBR，R3是该叶子节点的父节点，其代表的空间区域R3就是R8、R9和R10的MBR，重复这样的过程，直到每个节点对应的数据量在给定阈值范围内时就构成了最终的R树。

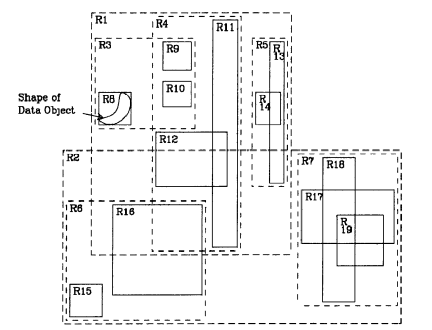
图 1 R树个节点对应的空间范围

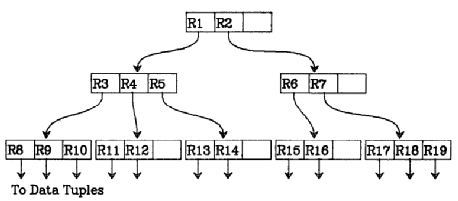
图 2 R树示例

在进行空间搜索时，比如给定空间范围S,我们想要找到与S在空间上相交的数据。这里R树加速查询的思想是尽量访问较少的节点，在查询时，假如S与某个节点对应的空间范围不相交，那么该节点对应的所有子节点就可以不必访问了，因为子节点表示的空间范围包含于父节点代表的空间范围。搜索过程就是树从上到下的遍历过程，只是可以根据上述性质进行剪枝。在到达叶节点时，我们找到叶节点中符合空间约束的记录，放入最终的结果集中。

3 K-D树

K-D[2]树是一棵二叉树，其中每个节点存储了一个k维的点，主要用于空间划分和k最近邻（KNN）搜索等问题。

K-D树的构造过程也就是空间划分的过程。构造过程主要有两点值得注意：划分维度的选择以及划分依据。这里介绍其中最简单的一种构造方式：我们交替地选择划分维度，然后以该维度对应的中位数为划分依据，将空间划分成两部分。

这里我们用二维的K-D树举例说明K-D树的构造过程，假如我们有(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)这些数据，每个数据对应了二维区域中的一个点。我们这里假设首先选择X维度进行划分，可以发现数据集中X维度的中位数为7，对应的点为（7,2），可以把空间划分成两部分，即在X维度上小于7的部分和大于7的部分，对应的K-D树就是以(7,2)为根节点，X维度上小于7的数据放到该节点的左子树，其余放到右子树。第二次我们选择Y维进行划分，划分过程与上述类似。重复这样的过程，直到叶节点中只包含一个数据时停止划分，该数据集对应的K-D树如图 3所示。

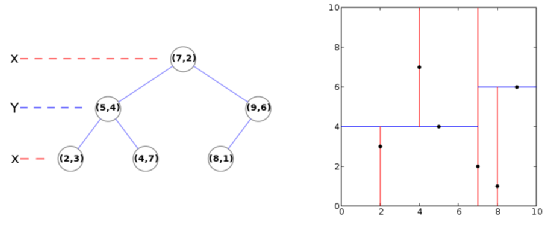
图 3 k-d树示例

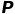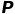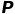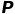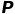接下来介绍如何利用K-D树进行最近邻搜索。假如给定点(3,4.5)，想要找到距离它最近的点，数据集与上个例子相同。这里我们首先找一个与相隔较近的叶节点，过程如下：首先访问根节点，此时划分维度为X,，划分的值为7，而3<7，因此我们接下来访问左子树，通过类似的过程最终到达叶节点(4,7)，由于这两点位于同一个划分区域内，因此(4,7)很可能就是最终的答案。这里首先假设(4,7)离最近的点，然后以为圆心，到(4,7)的距离为半径画一个圆，对应图 4中红色的圆，那么，最终的答案一定位于该圆之中。接下来进行回溯，发现(5,4)所对应的区域与该圆相交，因此对(5,4)进行距离的计算，发现该距离更小，因此将候选答案更新为(5,4)，更新后的圆就是图 4中绿色的圆。在访问完(5,4)后，由于(5,4)的左子树对应的空间区域与绿色的圆相交，因此再对(2,3)进行计算。在回溯到根节点后搜索停止，最终的答案就是点(2,3)。

假如想要进行KNN搜索，即找到与某个点最近的k个点，过程与搜索单个点时类似，不过需要维护一个优先队列进行答案的更新[7]。

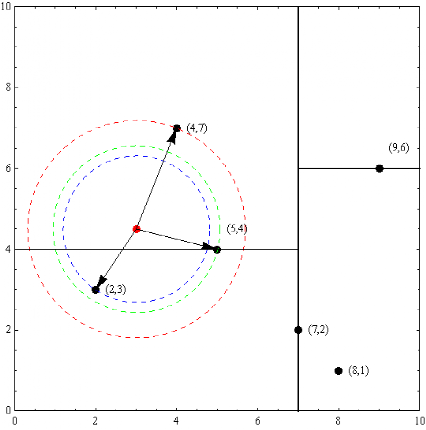
图 4 K-D树搜索过程

4 四叉树

四叉树[3]是一种树形的数据结构，其中每一个节点都有0个或4个子节点。构建四叉树时，是递归地对整个空间区域进行划分，划分成四个相同的子区域，直到每个子区域中的数据量小于给定的阈值。如图 5左半所示，初始的空间中有9个点，假如阈值为1。由于此时空间的数据量为9>1，故将该空间划分成四个子空间，即橙色部分。之后发现左上角的子空间的数据量为2>1，故再进行一次划分，重复这样的过程后，得到的四叉树如图 5右半所示。

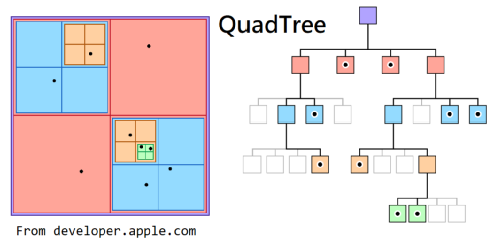
图 5 四叉树

在进行空间搜索时，比如给定空间区域S，我们想要知道哪些点位于S之内。搜索过程与R树类似，依然是从根节点向下搜索，碰到与S不相交的节点就进行剪枝，到达有存储数据的节点后就将满足空间约束的数据放入结果集中。

5 空间填充曲线

空间填充曲线是一条可以穿过任意维空间中所有点的曲线[9]，可以利用空间填充曲线对数据进行降维。在用作空间索引时，我们首先将空间进行划分，之后利用空间填充曲线对划分后的网格进行编号达到降维的效果。降维后就可以利用一些一维的数据结构进行索引，比如存成一维的ID，利用B树进行索引。

为了提高空间查询的效率，我们希望原空间上越接近的点，在降维后依旧接近。接下来本文首先介绍基于Z曲线的空间索引[10]。

如图 6左上角所示，一阶的Z曲线是将空间划分为四个相同的子区域，之后将各个区域的中点以Z字形连接起来得到。二阶的Z曲线，如图 6右上角所示，是将划分好的四个子区域分别再次划分成四份，并分别建立一阶Z曲线，最后将各个Z字首尾相连。重复这样的过程，可以得到任意阶的Z曲线。

图 6 Z曲线

在划分区域后，根据Z曲线的顺序，我们进行从0开始的递增编号，如图 7所示。假设我们对X轴和Y轴也进行编号，可以发现：将Y轴的编号与X轴的编号进行交叉编号后得到的编号恰好就是Z曲线对应的编号，这就是GeoHash降维所采用的方法。

通过GeoHash可以将点编码成一维的ID，将空间区域转换成一个或多个ID的范围。在进行空间搜索时，首先将空间区域转换成ID的范围，之后可以利用一维的索引进行范围搜索得到候选答案，从候选答案中筛选出符合空间约束的数据就可以得到最终的答案。之所以要进行进一步的筛选是因为GeoHash本质上是将一个点看成了一个区域，因此直接根据ID进行筛选会有少量误差。

图 7 Z曲线编号

然而，Z曲线存在一定的突变型。如图 8所示，标记上颜色的点在原空间上并不相近，然而在编码后却是相邻的。突变性会使得将空间范围转换成ID范围时存在较大的误差。

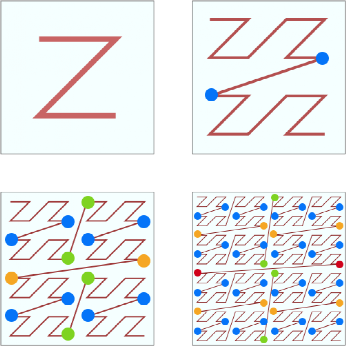
图 8 Z曲线的突变性

在空间填充曲线中比较好的代替方法是希尔伯特曲线，如图 9所示，可以发现它并没有如Z曲线一般的突变性。

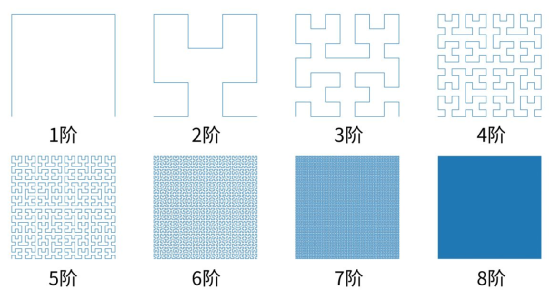
图 9 希尔伯特曲线

目前基于希尔伯特曲线的空间索引有Google的S2算法[8]。该算法的具体流程如图 10所示：

S2算法进行空间查询的过程与GeoHash类似，依旧是将空间区域转换成对应的ID范围后进行范围搜索，最后进一步筛选出符合空间约束的数据。

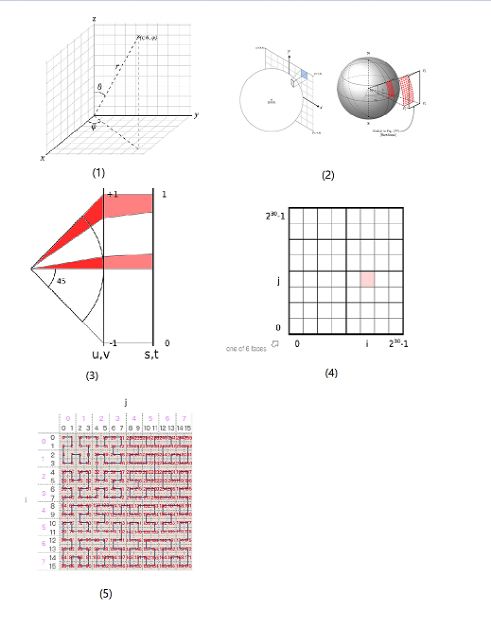
图 10 流程

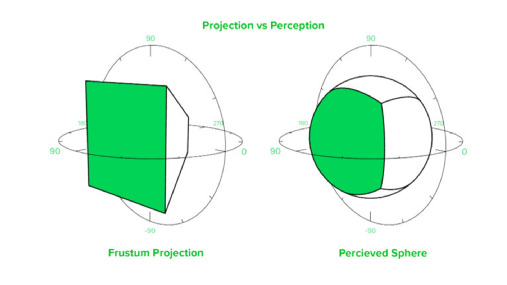
图 11 球面投影

参考文献：