一文读懂遗传算法（附源代码）

        顾名思义，遗传算法正是一种模仿生物学遗传规律的启发式求解方法。科学理论研究中存在着许多与优化及自适应相关的问题，正类似于自然界生物的进化规律，物竞天择，适者生存，使得更适应生存环境的物种留存下来。

        遗传算法通过选择、交叉、变异等操作，来模拟生物界的遗传过程，进过多轮的迭代从而试图求得问题的最优解。由于其简便而通用的性质，遗传算法已被广泛应用于自适应控制，机器学习，管理决策等领域。本文简介最基本的遗传算法，并通过一个实例来探索遗传算法各个参数对最终迭代结果的影响，以便对遗传算法有更深刻的理解。最终附上源代码，供初学者参考。

一．简介：

        基本的遗传算法包括：编码、解码模块，适应度函数模块，遗传模块（选择，交叉，变异），以及主函数模块。

1. 编码、解码模块：

        遗传算法的基本操作对象是染色体，多个染色体组成种群。而编码模块相当于一个外部数据转换成染色体的接口，解码模块相当于将染色体还原成数据的接口。

编码方式有很多种，最常见的是01编码，即用一串二进制数字表示一个变量，例如自变量x的取值范围是[0,1]，实数。假如我们用8位的二进制数来表示x，x=1对应11111111，x=0对应00000000，即我们用长度为8的染色体，表示了变量x。

        而解码是编码的逆操作，假如遗传算法结束后所得染色体为：10101101，则我们可以根据编码时的对应规则，将其还原为对应的x值。

2. 适应度函数：

        即表示一条染色体适应环境的程度，它是一个函数，输入一个染色体，输出一个值，其值越大，代表此染色体更适合生存。当面对的是求最大值问题时，适应度函数可取与目标函数相同。当所求为最小值时，可取适应度函数为目标函数的倒数。

3. 选择：

        选择用于交叉的父母染色体，输入为整个种群，输出为两个染色体。

        而选择的规则有很多，最基本的是赌轮盘法，即种群中适应度值较大的，被选中的概率越大。编程实现时，可先将种群中所有染色体适应度函数计算出来，然后求和，再用每个适应度函数除以和即归一化为概率分布，随机产生0-1之间的随机数，找出此随机数对应的适应度区间，进而确定所选的染色体

4. 交叉：

        将已选择的两个染色体，直接交换部分片段。那具体要交换哪个片段呢？随机在染色体上取一个位置，将此位置后的片段互换。此为单点交叉，若随机选择两个位置，将位置间的片段交换，成为两点交叉。多点交叉类似。输入：2个染色体，输出：2个新染色体。

5. 变异：

        随机选取染色体的一个位置，将此位置处的值在定义域内随机替换为一个新值，例如若是01编码，假如选取位置处的值是1，则变为0，是0则变为1。

输入：一个染色体，输出：一个染色体。

关于具体的遗传算法实现逻辑有很多种，本文采取的是其中一种。有关于遗传算法更多的信息可参考《遗传算法原理及应用》

二. 举例

题目：

Obj: max  y=100*(x1²-x2)²+(1-x1)²

S. t. -2.048<=xi<=2.048     (i=1,2)

已知解析解：3897.9342（局部极大点），3905.9262（全局最大值）

参数：

单纯的遗传算法由于择优的法则，种群中的多样性逐渐减小，容易使得算法陷入局部最优解，所以通常会在传统的遗传算法中加入“模拟退火”，来帮助算法跳出局部最优，使得其获得更好地全局搜素能力。关于“模拟退火”的原理会在下一篇文章详细介绍，故此处不再赘述。

迭代过程如下图，最终结果：3905.926227，可见与解析解一致，精度也足够。

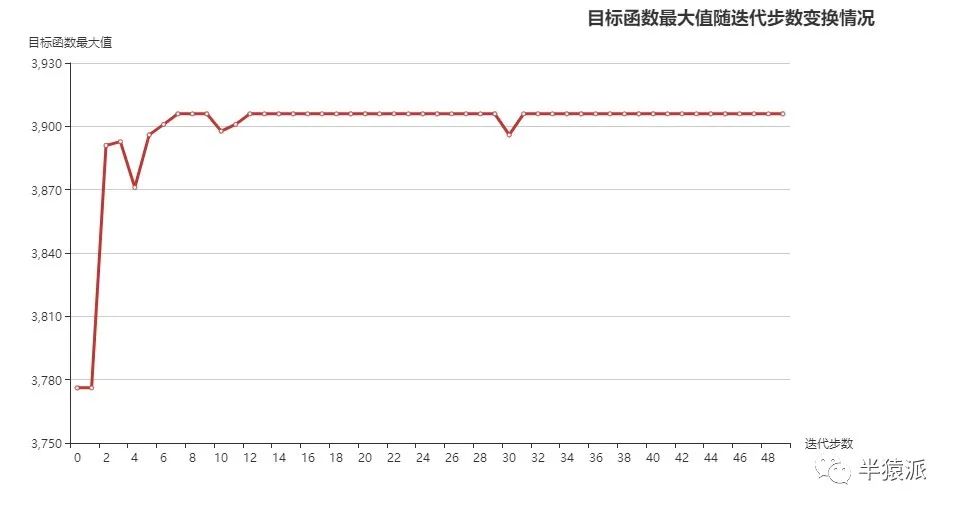
接下来我们控制变量，分别改变一下不同的参数，看看得到的结果有什么规律。基础

参照组：

1.模拟退火的影响。分别打开和关闭模拟退火，并进行五次实验，得到结果如下：

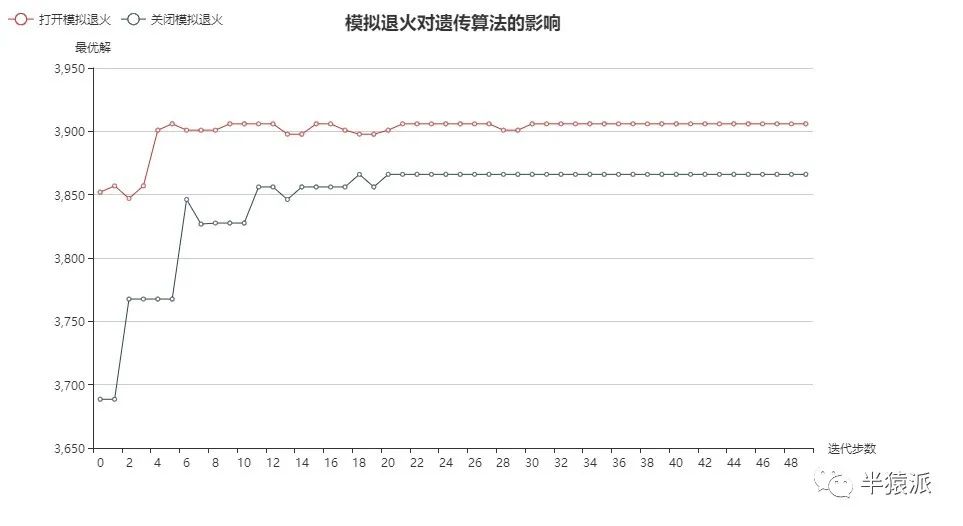
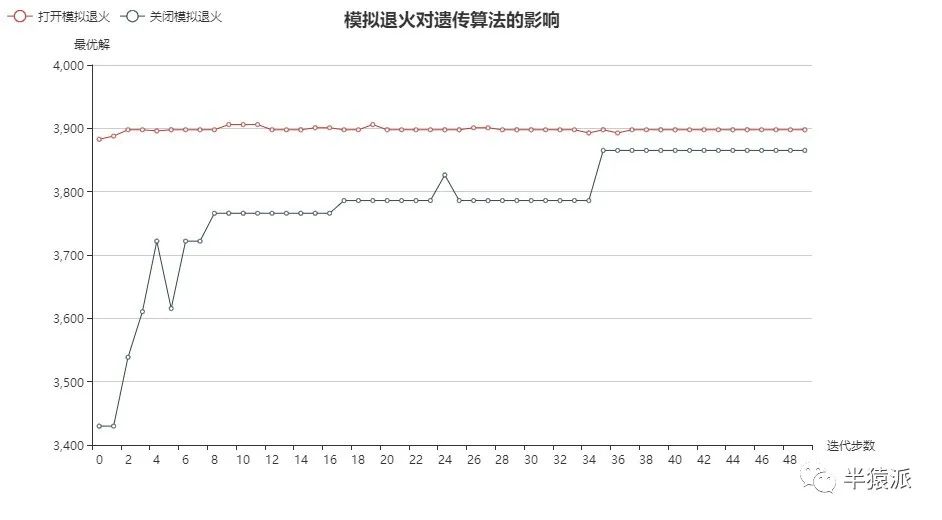
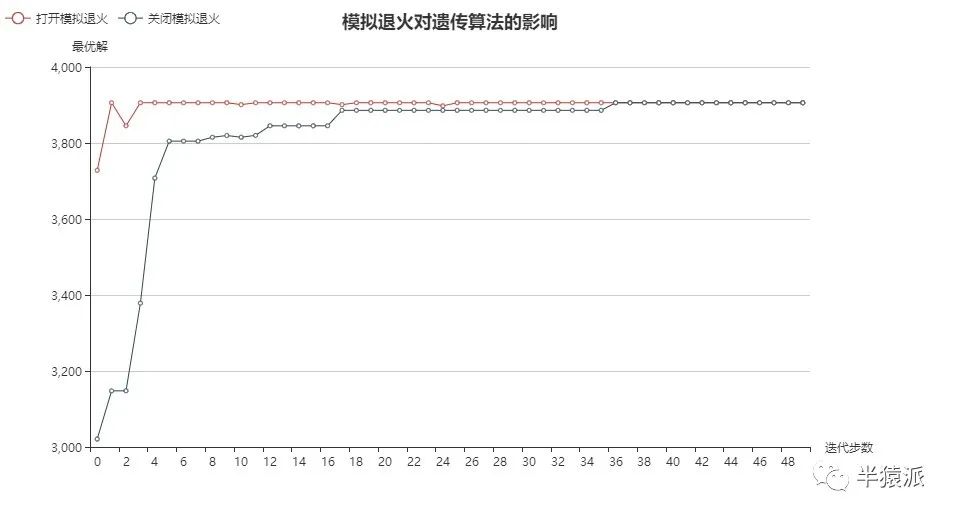
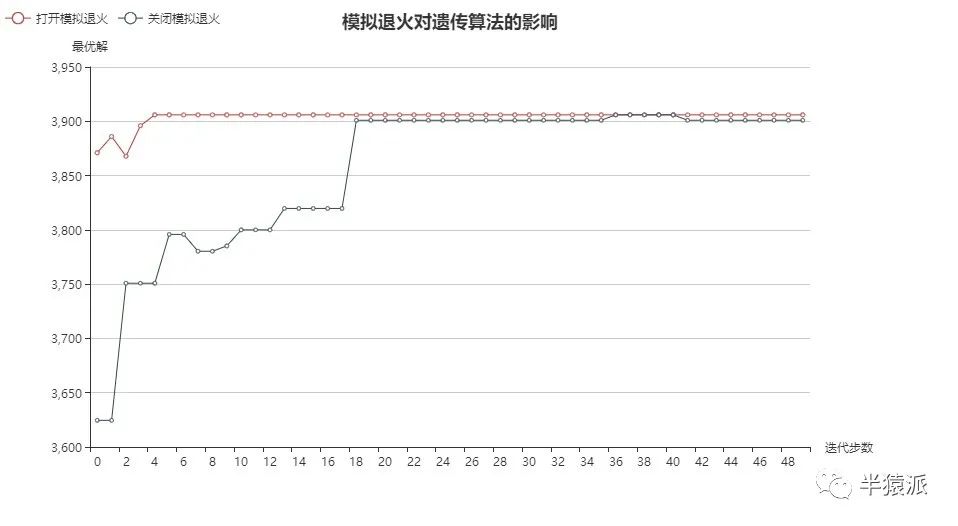
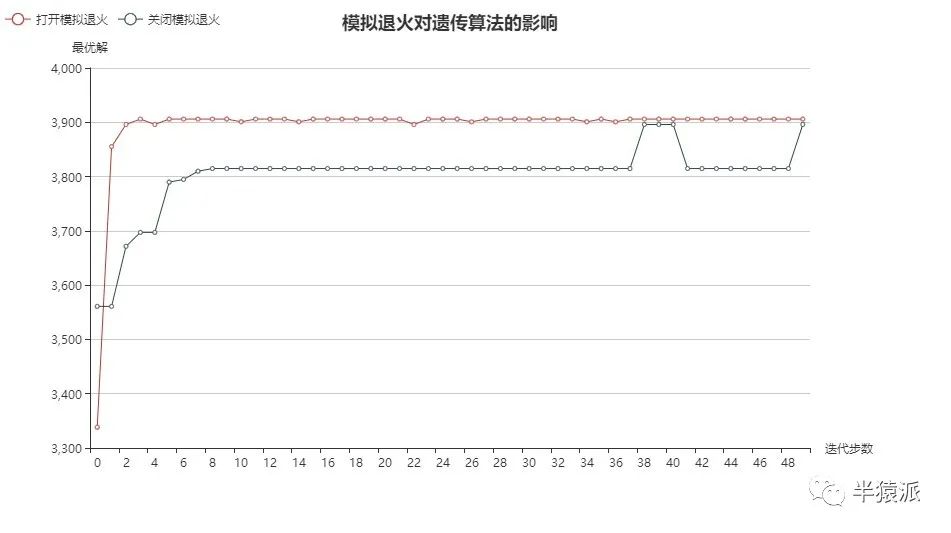
结论：模拟退火能够加速算法收敛；能有助于跳出局部最优解，有更好地全局寻优能力。

2. 种群数量分别取：10，20,40,60,80,100，avg是目标函数在种群中的平均值，max为目标函数在种群中的最大值，即最优染色体的适应度函数值。

所得结果如下：

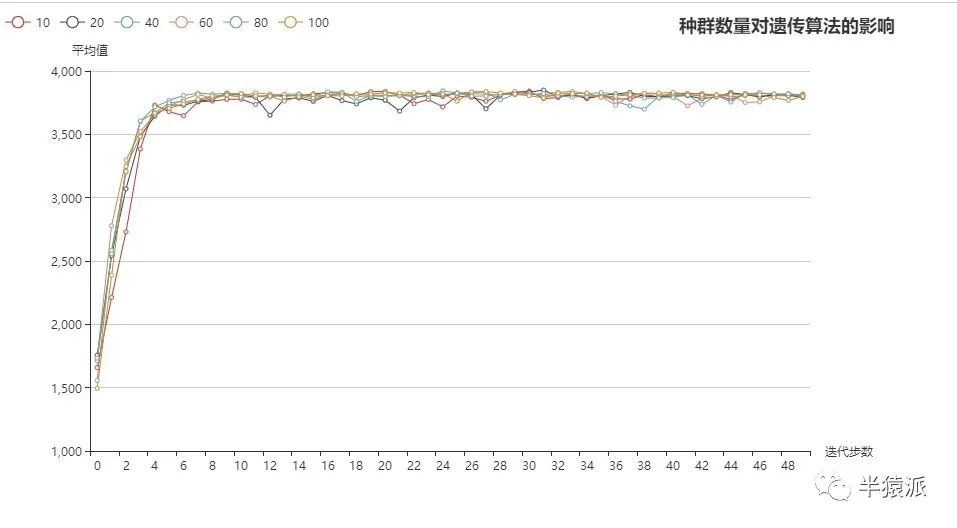
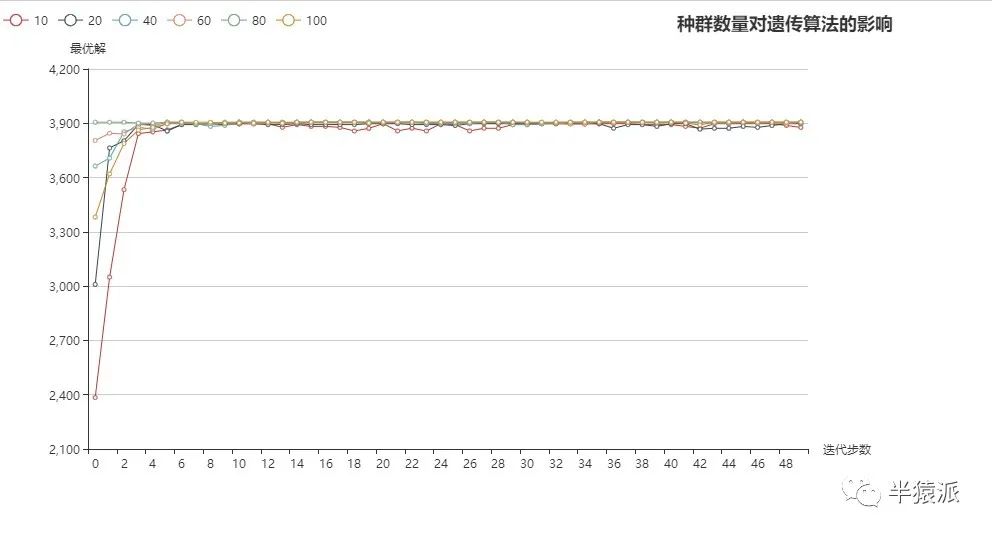
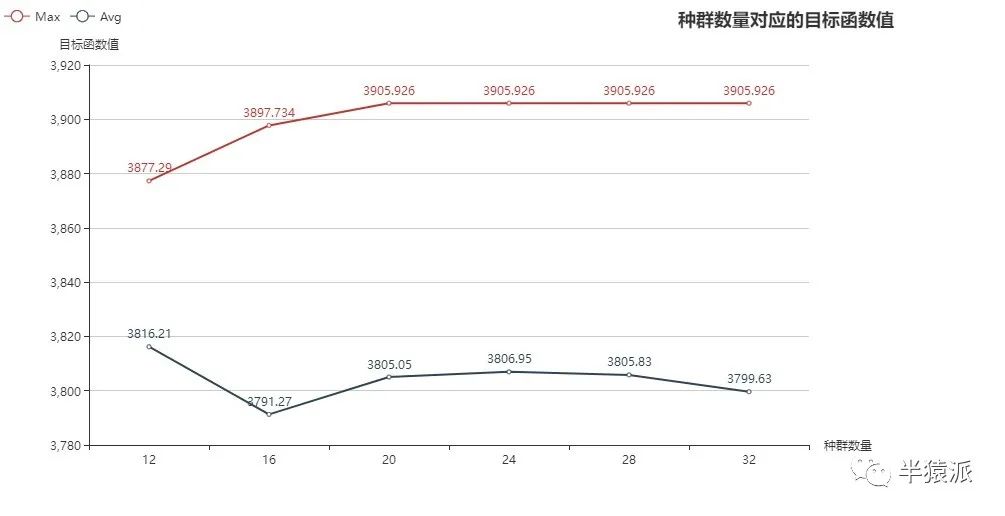
结论：种群数量过小时，算法可能无法找到最优解；种群数量过大时，由于迭代循环数更多，必然花费更多得时间。

3. 编码长度：12,16,20,24,28,32，种群数量：5,10,40,80,160,320

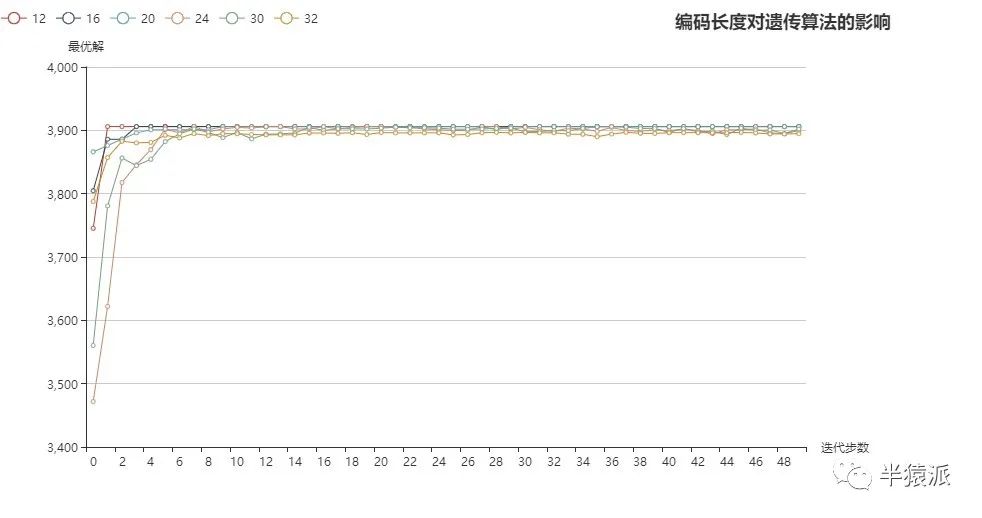
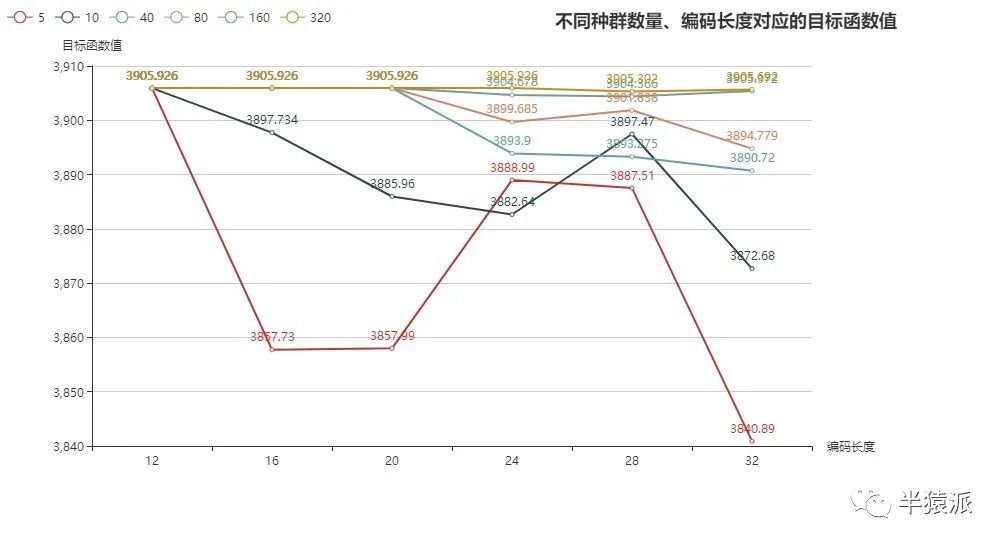
结论：编码长度在一定情境下可理解为变量的精度，而种群数量在一定程度上可以理解为解空间的大小。由图中可以看出，对于更大的编码长度，需要更大的种群数量来支撑。所以在设计遗传算法的参数时，种群数量和编码长度要相互匹配。根据问题的复杂度，种群数量与编码长度的比值也许可以作为算法参数选择的依据。

4. 交叉概率：0,0.2,0.4,0.6,0.8,1.0；变异概率=0

（1）模拟退火关闭：

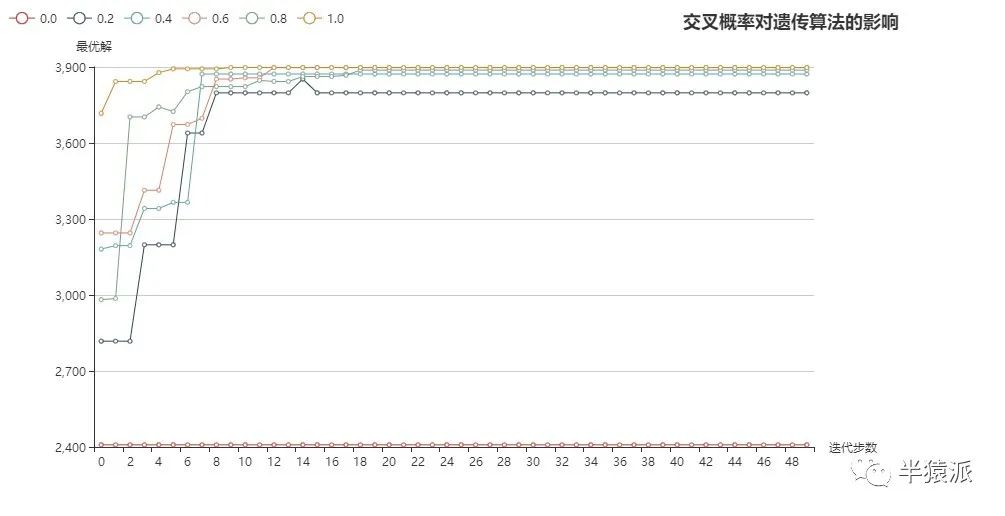
（2）模拟退火打开：

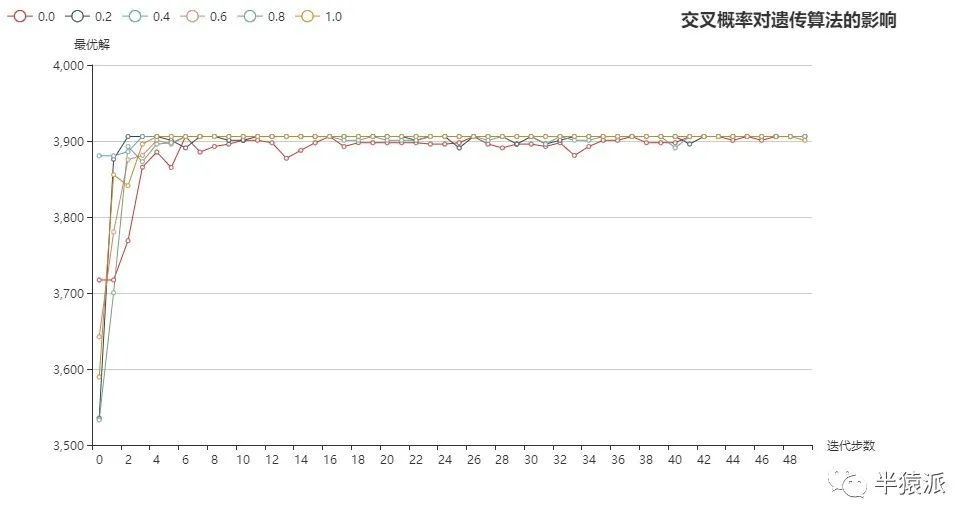
（3）对比曲线：

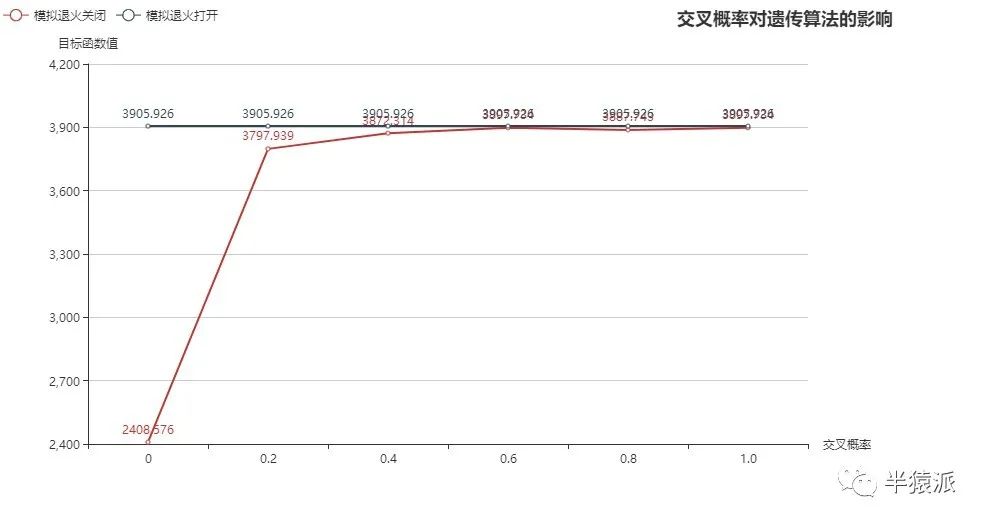
结论：

（1）由上图可看出，当模拟退火关闭，交叉概率为0时，种群没有新个体生成，所求的的解一直相同，且距离解析解距离较大，随着交叉概率的增加，算法逐渐找到局部最大值，但大部分算例无法找到全局最优。

（2）因为模拟退火会产生新的染色体，所以当模拟退火打开时，很快收敛到全局最优；当交叉概率较小时，收敛曲线波动较大。

5.变异概率：0，0.2,0.4,0.6,0.8,1.0；交叉概率=0

（1）模拟退火关闭：

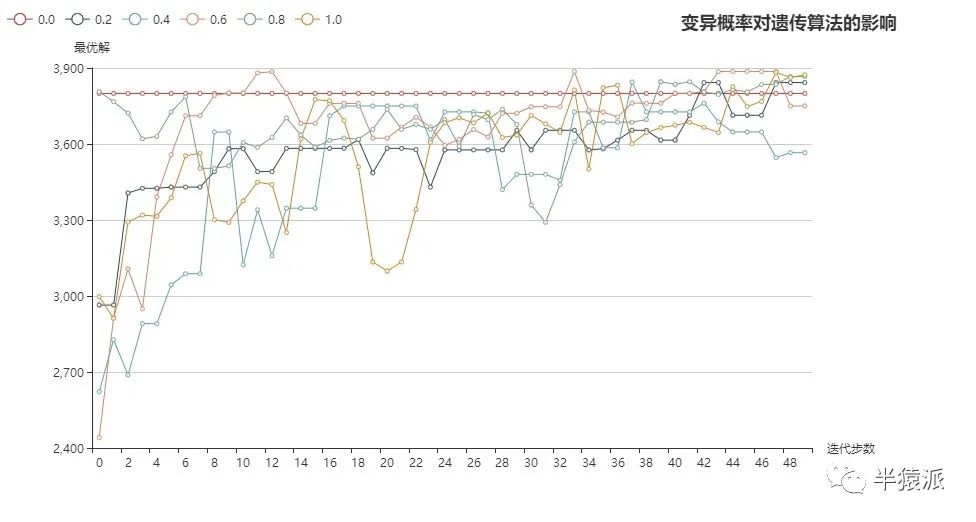
（2）模拟退火打开：

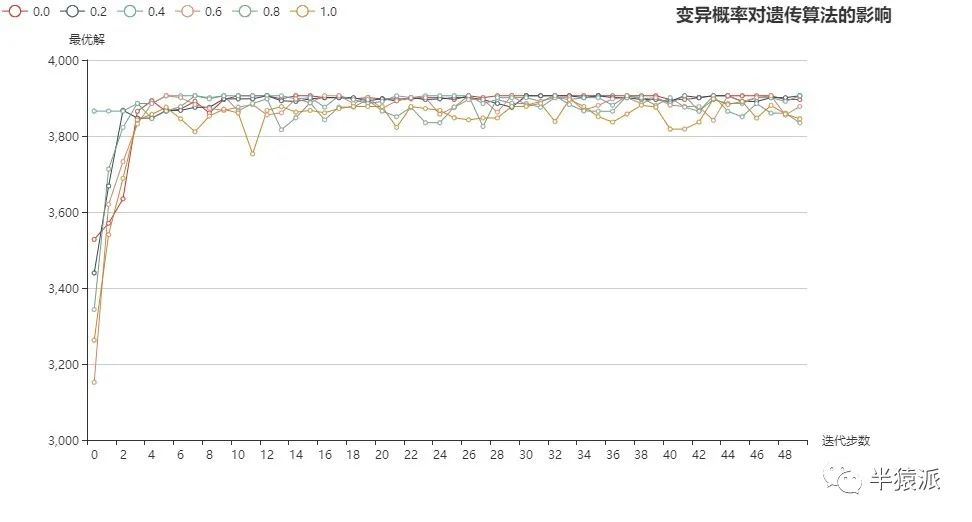
（3）对比曲线：

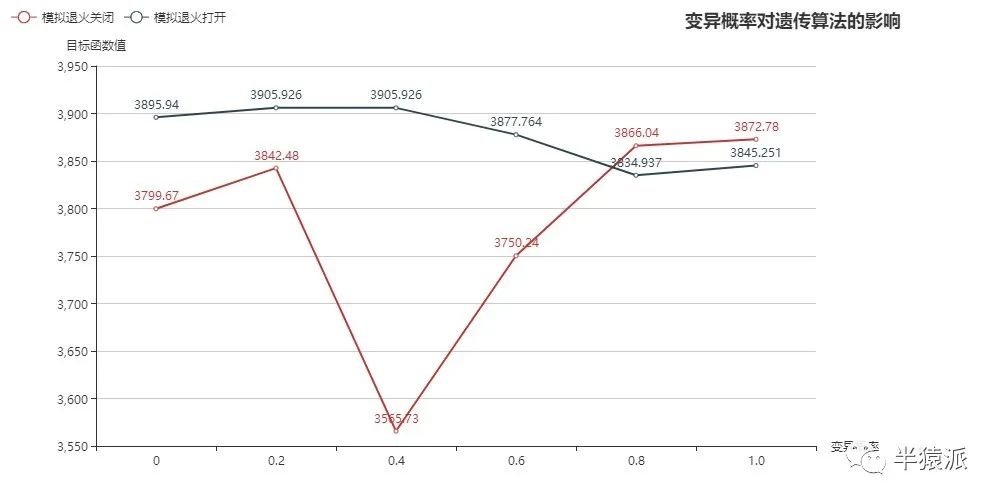
结论：（1）单纯通过变异产生更优染色体的效率较低；

（2）模拟退火+变异产生更优染色体的效率较（1）有所提高，但是低于交叉的效率。

三. 代码展示：

1. 适应度函数

def FitnessFun(Chrom_In):
    x1,x2=encoding(Chrom_In)
    Fitness=100*pow((pow(x1,2)-x2),2)+pow((1-x1),2)
    return Fitness

2. 初始化种群

def init():
    global Chrom_N
    global Fit_np
    Chrom_N=np.random.randint(0,2,(N_num,L))            #初始化种群


    for i in range(N_num):
        Fit_np[i]=FitnessFun(Chrom_N[i])                #初始化种群适应度
    return 0

3. 解码：因为我们是随机初始化种群，为方便起见，在初始化时就应经是20位二进制数的染色体，相当于已经编码完成，故本例并没有单独的编码模块。若实际应用时变量的值需要读取excel的数据，则需要单独的编码模块。

def encoding(Chrom_In):
    sum_n1=0
    sum_n2=0
    for i in range(int(L/2)):                       #由二进制转换为十进制数
        sum_n1 += Chrom_In[int(L/2)-i-1]*pow(2,i)
        sum_n2 += Chrom_In[L-i-1]*pow(2,i)
    x1=4.096*sum_n1/1023-2.048                      #求得x1,x2值
    x2=4.096*sum_n2/1023-2.048
    return x1,x2

4. 选择

def Select(ChromS_In):


    P_array=(Fit_np/(Fit_np.sum())).cumsum()    #产生累积的概率分布
    Sel_random=np.random.rand(2)                #赌轮盘法选择两个染色体
    Sel_index=[]
    for s in Sel_random:
        for i in range(N_num):
            if s<P_array[i]:
                Sel_index.append(i)
                break
    return [ChromS_In[Sel_index[0]],ChromS_In[Sel_index[1]]]

5. 交叉

def Crossed(Select_ChromS_In):
    Chrom_i=Select_ChromS_In[0].copy()
    Chrom_j=Select_ChromS_In[1].copy()
    P_1=np.random.randint(0,L)


    Chrom_i[0:P_1],Chrom_j[0:P_1] = Chrom_j[0:P_1],Chrom_i[0:P_1]
    Chrom_best=Chrom_i      #交叉产生两个染色体并和父母染色体比较
    if FitnessFun(Chrom_best)<FitnessFun(Chrom_j):
        Chrom_best=Chrom_j
    for i in range(2):
        if FitnessFun(Chrom_best)<FitnessFun(Chrom_Selected2[i]):
            Chrom_best=Chrom_Selected2[i]   #返回1个最优染色体
    return Chrom_best

6.变异

def Mutation(Chrom_In_):
    Chrom_In=Chrom_In_.copy()
    P_1=np.random.randint(0,L,1)
    if Chrom_In[P_1]<1:
        Chrom_In[P_1]=1
    else:
        Chrom_In[P_1]=0


    return Chrom_In

上述为遗传算法各部分的实现函数，如果大家觉得看起来麻烦，点击关注后，回复"GA”，获取整个源代码。

四 .结语

        遗传算法可应用于各种函数优化的场景，思路原理简单。感兴趣的同学可以关注本公众号，持续更新，共同学习。

        以上所有文字，图片，代码均属原创，如果觉得不错，欢迎分享，但请注明出处。