一、引言
分享知识+推广我的Python书。
上次本号转载了中国科技术语公众号的文章《冯志伟 | 术语研究中的最小编辑距离》,现在介绍最小编辑距离的Python程序实现,介绍两种方法:递归法和动规法,另外还将对比两者的时间效率。
《Python程序设计(基于计算思维和新文科建设)》,ISBN:9787121435577,胡凤国,电子工业出版社,2022年6月。本书是电子工业出版社在国内较早采用纸质版+电子版的创新图书发行模式的第一次尝试。本书是这套创新图书的纸质版部分,与之内容互补的电子版图书将稍后出版。基础篇介绍Python程序设计的入门知识,共12章,包括:⑵ Python软件的安装和Python程序运行;⑶ Python的基本概念(对象、数据类型、表达式、内置函数);排错篇总结初学者常遇到的错误并介绍程序调试方法,包含2章:与本书内容互补的电子版图书包含文本篇和应用篇两部分:文本篇:介绍字符集、编码和文本文件读写的知识,包含了对国家规范《通用规范汉字表》8105个汉字当中难以输入和难以显示的汉字的处理。应用篇:介绍Word、Excel、PPT、PDF、图片等常用办公文件的处理,是大家提高办公和科研效率的好帮手。本书配套有详细的PPT和教学大纲,还有全部例题的程序代码和绝大部分思考题的程序代码。本书配套PPT里面还加入了配套电子版图书中的部分内容,比如字符集和编码,不同编码的文本文件的读写,Word、Excel、PPT、PDF等一些常用办公文件的读写。1、大学文科生, 可选本书当Python教材或自学Python的参考书。2、大学理工科学生, 可选本书当自学Python的参考书。可拿本书当工具书,本书的配套程序会为您节省效率,在当前大数据和新文科的背景下,本书可以为相关领域的量化研究提供技术支持。本书配套的电子版图书中的编码和文本处理知识也可以作为理工科教师和科研人员处理文本数据的参考资料之一,毕竟专门开辟章节介绍国家标准《通用规范汉字表》汉字处理的程序设计图书并不多见。
本书有专门的海龟画图章节,有大量的有趣数学题目,可以培养学生的计算思维,适合对编程感兴趣的中小学生阅读,也适合打算让娃参加编程辅导班的家长朋友参考。本书在各大实体书店和网店均有销售。尤其在电子工业出版社天猫旗舰店销售火爆,月销量100+。京东、天猫、当当的购买渠道如下(可扫码直达购买页面)。我们把两个字符串之间的最小编辑距离定义为把源字符串编辑为目标字符串所需要的代价之和,这里的编辑仅限于三种操作:删除、插入、替代,每次编辑操作只能且必须操作一个字符。最小编辑距离公式如下(由于公众号上的公式排版比较乱,小编另找了一个清晰版的公式,来自冯志伟先生著的《自然语言处理简明教程》):

上述公式中的 distance[i, j] 表示目标字符串的前 i 个字符组成的子串跟源字符串的前 j 个字符组成的子串之间的最小编辑距离。我们把插入和删除的代价定为1,替代的代价定为0或2(当两个字符相同时,替代的代价为0,否则为2)。
动规法是动态规划法的简称,求最小编辑距离可以用动规法来求解。我们这里不介绍动态规划算法,只是根据公众号文章里面提到的算法来求解两个字符串之间的最小编辑距离。跟递归法一样,我们把插入和删除的代价定为1,替代的代价定为0或2(当两个字符相同时,替代的代价为0,否则为2)。
跟递归法不同的是,动规法必须设置一个矩阵d,这个矩阵有m+1行n+1列,这里m是源串s的长度,n是目标串t的长度。矩阵d的元素d[i][j]表示源串s的前i个字符构成的子串跟目标串t的前j个字符构成的子串之间的最小编辑距离。
显然,当 i 为 0 时,d[i][j]=j;当j为0时,d[i][j]=i;当i和j都不为0时,d[i][j]的值要根据前面提到的最小编辑距离公式来计算。我们首先给矩阵d的第0行和第0列各元素赋值,然后就可以设定一个两重循环,逐个给d中的其它元素赋值。最后得到的元素d[m][n]的值就是源串s和目标串t的最小编辑距离。
两个算法的结果应该是一样的,我们重点看它们的时间效率的对比:

上述代码的运行结果如下:
源 串:intention
目标串:execution
递归法用时:0.76997 秒
非递归法用时:0.0 秒
源 串:intentiona
目标串:executiona
递归法用时:4.2706 秒
非递归法用时:0.0 秒
源 串:intentionaa
目标串:executionaa
递归法用时:23.464 秒
非递归法用时:0.0 秒
源 串:intentionaaa
目标串:executionaaa
递归法用时:131.82 秒
非递归法用时:0.0 秒
我们看到,源串和目标串的长度每增加1,递归法求解耗费的时间大约是原来的5倍多,而动规法耗费的时间可以忽略不计。
可见,在最小编辑距离这个问题的求解方面,递归法只有理论上的意义,实际中是不可行的。
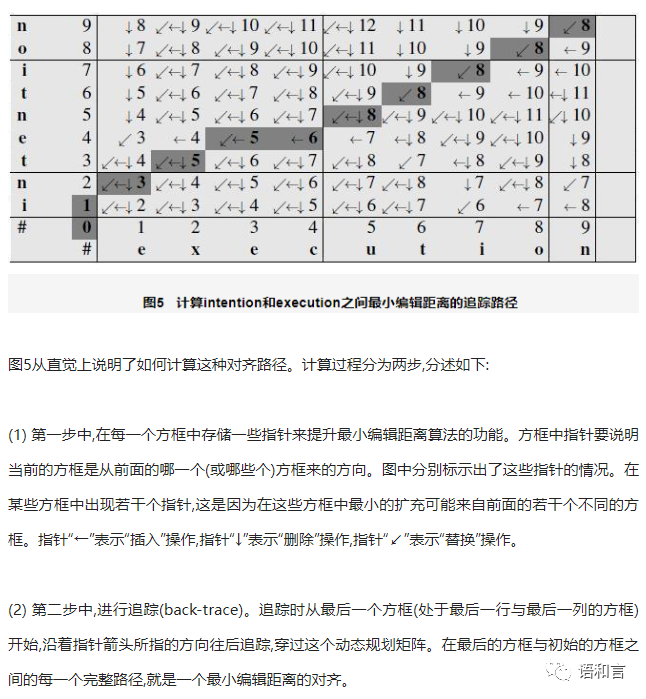
这个追踪路径我们称之为最短编辑路径,我们可以写一个Python程序来求出把源串变成目标串的一条最短编辑路径。由于最短编辑路径可能不止一条,我们可以把程序修改一下,使之能求出所有的最短编辑路径。
最短编辑路径的一个直接应用就是比较两篇文本的异同(以行为基本的比较单位),文本编辑软件EmEditor就有这样的一个功能,我们不知道该软件比较的算法是什么,但我们知道用最小编辑距离和最短编辑路径可以比较两篇文本的异同。感兴趣的童鞋可以考虑一下把源串变成目标串的最短编辑路径这个问题,并用Python程序实现之。欢迎跟图书《Python程序设计(基于计算思维和新文科建设)》的作者胡凤国老师进行交流,作者电邮:cuchufengguo@163.com ,也可以给公众号留言进行交流。欢迎关注微信公众号“语和言”,本公众号将不定期发布对本书Python知识点的解读和补充内容。
语和言公众号还有读者交流群,经常跟作者交流的读者朋友可以入群一起讨论问题。














