Table of Contents

• 一. 线性规划问题的数学模型
• 1.1 例子
• 1.1.1 例1
• 1.1.2 例2
• 1.1.3 例3
• 1.1.4 例4
• 1.2 线性规划的数学模型概要
• 二. 线性规划的解
• 2.1 图解法
• 2.2 单纯形法
• 2.2.1 基本原理
• 2.2.2 从一个简单例子入手
• 2.3 解的类型
• 2.3.1 初始基本可行解的确定
• 2.3.2 例子
• 四. 线性规划模型的应用
• 4.1 案例:公交车司机
• 4.2 案例:生产计划问题
• 4.3 案例:套载下料问题
• 参考:

一. 线性规划问题的数学模型

1.1 例子

1.1.1 例1

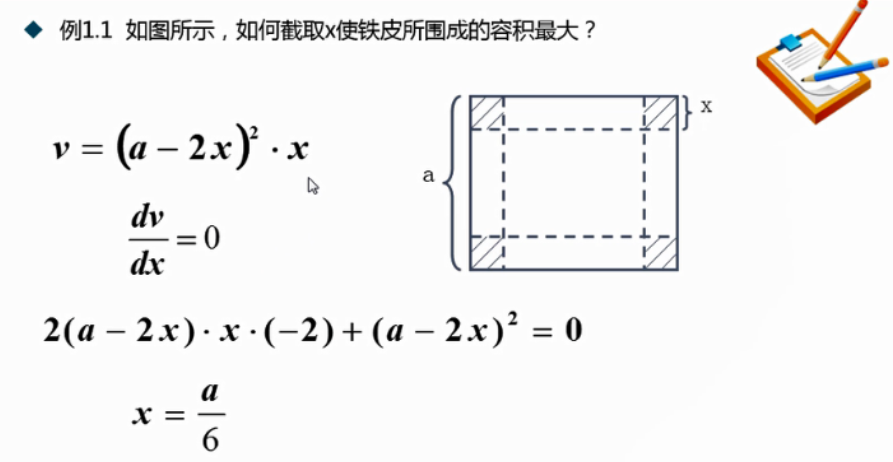
设四个角截去的小正方形边长为X.
则有盒子的体积为:
V=(a-2X）*(a-2X)*X =a^2X-4aX^2+4X^3

V’=a^2-8aX+12X^2 =(a-2X)*(a-6X)
令V’=0得:X1=a/2； X2=a/6
又:V”= -8a+24X
当X1=a/2时,V”= 4a＞0,V有极小值0；
当X2=a/6时,V”= -4a＜0,V有极大值：
V极大=(2/27)a^3

1.1.2 例2

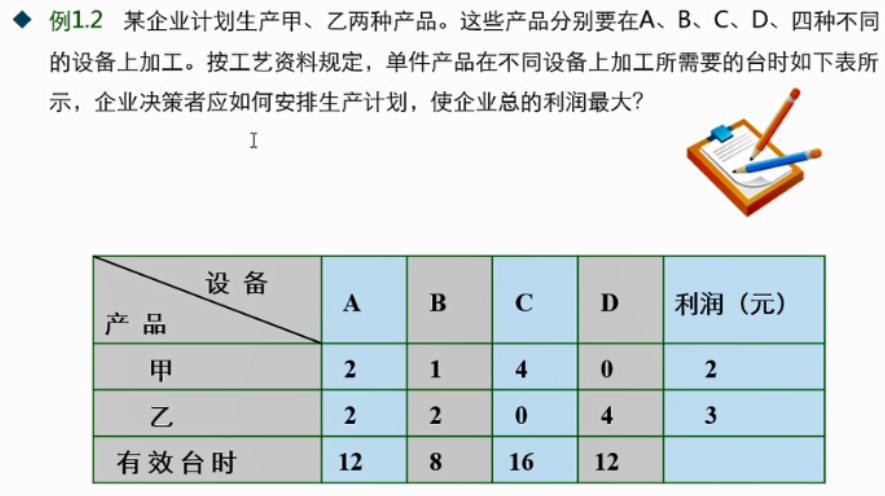
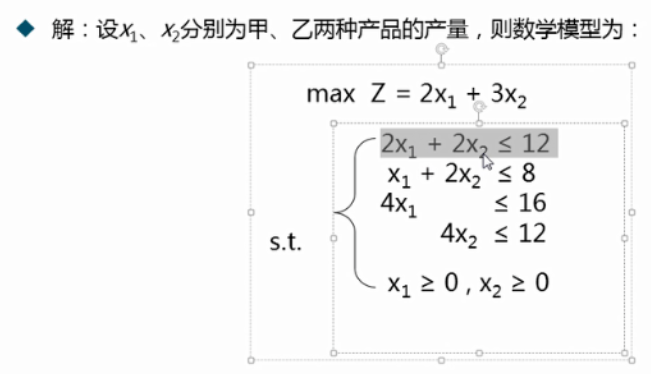
1.1.3 例3

例3区别于例1和例2，已经转换为了标准的数学公式

1.1.4 例4

通过矩阵来求最优解

1.2 线性规划的数学模型概要

三要素:

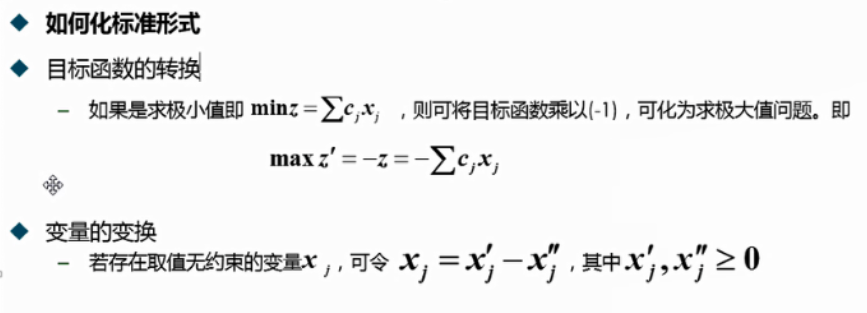
二. 线性规划的解

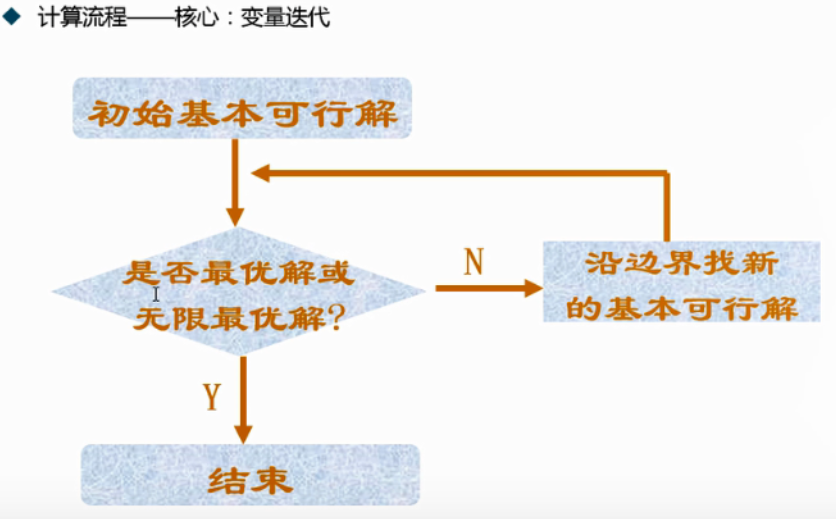
求解方法
图解法有点类似几何的解法
单纯形法有点类似代数的解法

2.1 图解法

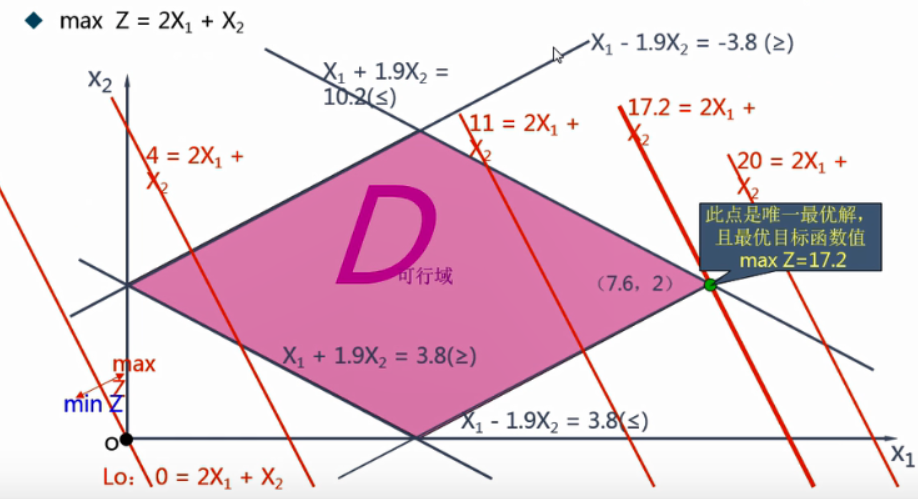
2.2 单纯形法

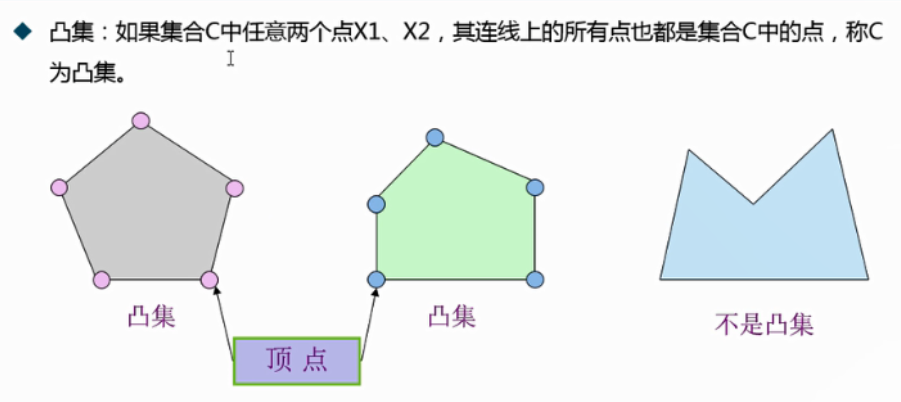
2.2.1 基本原理

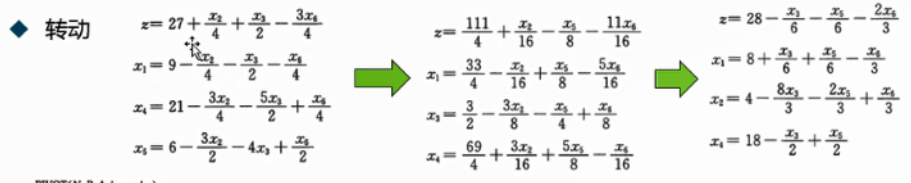
2.2.2 从一个简单例子入手

2.3 解的类型

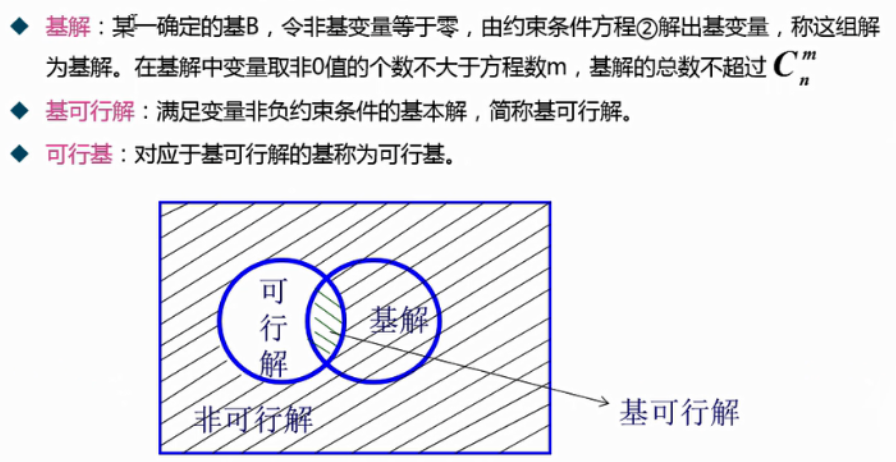
2.3.1 初始基本可行解的确定

最优性检验:

总结计算步骤:

2.3.2 例子

四. 线性规划模型的应用

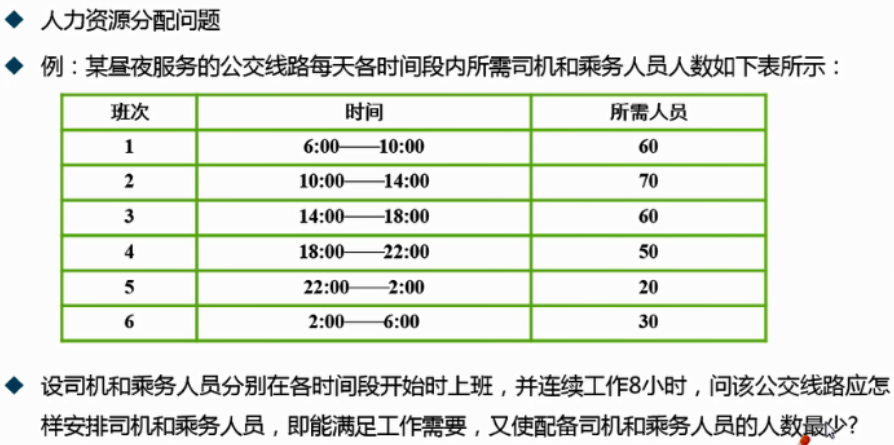
4.1 案例:公交车司机

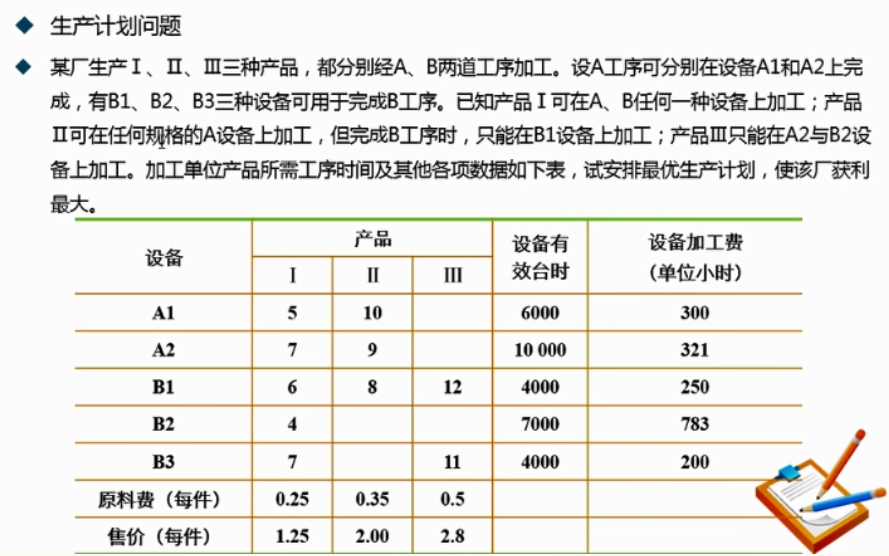
4.2 案例:生产计划问题

4.3 案例:套载下料问题

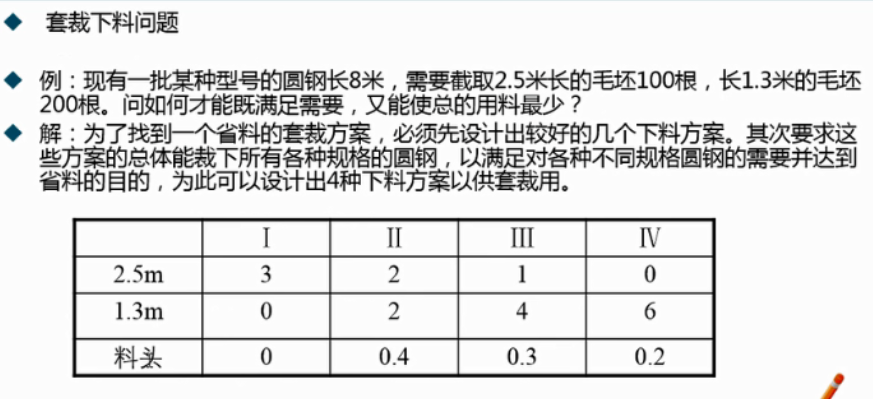
目标函数:
Min x1 + x2 + x3 + x4

约束条件:
3x1 + 2x2 + 3x3 + 0x4 >= 100
0x1 + 2x2 + 4x3 + 6x3 >= 200
x1,x2,x3,x4 >= 0

参考:

1. http://www.dataguru.cn/article-5747-1.html