前段时间看肉食动物的漫才脱口秀讲到龟兔赛跑的故事,别小看龟兔赛跑这么个故事,用到链表中能发挥很大的作用,不仅可以用来检测链表是否存在环路,还能提供断开环路的方法,这就是龟兔赛跑算法(tortoise-and-hare algorithm),也称为 Floyd 判圈算法(Floyd's cycle finding algorithm)。
算法原理
假设存在一个链表,有一只乌龟和一只兔子都从链表的头节点出发,乌龟每步移动一个节点,兔子每步移动 2 个节点。如果链表存在环路,那么兔子先进入环路,并在环路中绕圈圈,乌龟虽然慢点儿,但最终也会进入环路,两者的速度不一样,所以迟早会相遇,相遇了,那链表存在环路这个事儿就被检测出来了。

那如何把这个环路断开呢?咱们需要知道两个东西:
环路的起点在哪儿? 环路的终点在哪里? 不急,回到上面那张图,咱们先假设几个未知数:
T
——乌龟进入环路前经过的节点数;H
——乌龟走了 T 步后从环路开始位置到兔子位置的节点数;L
——环路中的节点数;从图1来看,T=4
(乌龟从哨兵节点出发),H=4
,L=5
。哨兵是链表的头结点,不存储值,用来简化边界条件。基于上述的设定,咱们可以推出两个重要事实:
乌龟走了 T
步后,兔子走了2T
步,意味着兔子在环路中走了T
步,此时兔子距离环路开始节点H
步。==>如果从环路开始节点移动T
个节点,那么距离环路开始节点 H 个节点。当乌龟进入环路时,兔子和乌龟相距 L-H
个节点,兔子每步比乌龟多移动 1 个节点,所以兔子将在L-H
步后赶上乌龟。当两者相遇时,乌龟移动了L-H
个节点,因此乌龟和兔子相遇的位置距离环路开始节点L-(L-H)=H
个节点。==>乌龟和兔子相遇的节点距离环路开始位置 H 个节点。
我们的目标是找到环路的起点和终点从而断开环路,但是L、T、H
的值都是未知的,怎么办?
有请龟小弟上场👏🏻,当乌龟和兔子在环路中相遇时,第二只小乌龟也就是龟小弟从哨兵节点出发,每步移动一个节点,兔子跑了那么多圈太累了不动了,前面的龟大哥继续每步移动一个节点。
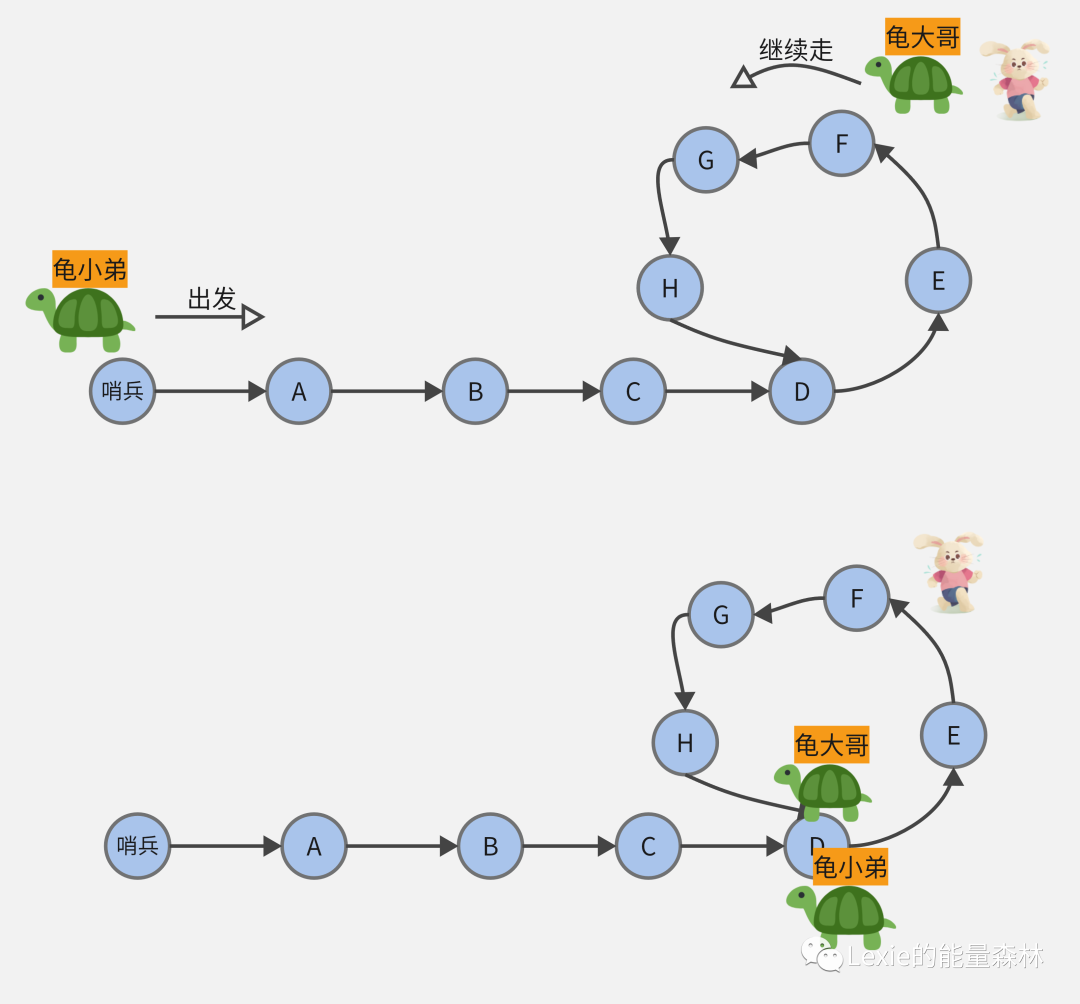
龟大哥和龟小弟最终在环路开始节点相遇。为什么恰好是环路开始节点呢?龟小弟走到环路开始节点需要走T
步,当龟小弟走了T
步后,龟大哥则是从相遇的节点也走了T
步,此时龟大哥的位置在哪儿呢?
先看重要事实1:如果从环路开始节点移动T
个节点,那么距离环路开始节点H
个节点。那么龟大哥此时应该距离相遇的节点H
个节点。
再看重要事实2:乌龟和兔子相遇的节点距离环路开始位置H
个节点。对了,龟大哥此时距离环路开始节点恰好H
个节点,所以当龟小弟走到环路开始节点时,龟大哥也正好走到了环路开始节点!
根据上述事实,可以推出:
环路的起点在哪儿?——龟大哥和龟小弟相遇的节点就是环路开始的节点。 环路终点在哪里?很好解决,龟大哥和龟小弟在环路起点相遇后,兔子休息够了,从和龟大哥的相遇点开始走,直到下一个节点为龟大哥,那么兔子所在节点即为环路终点。
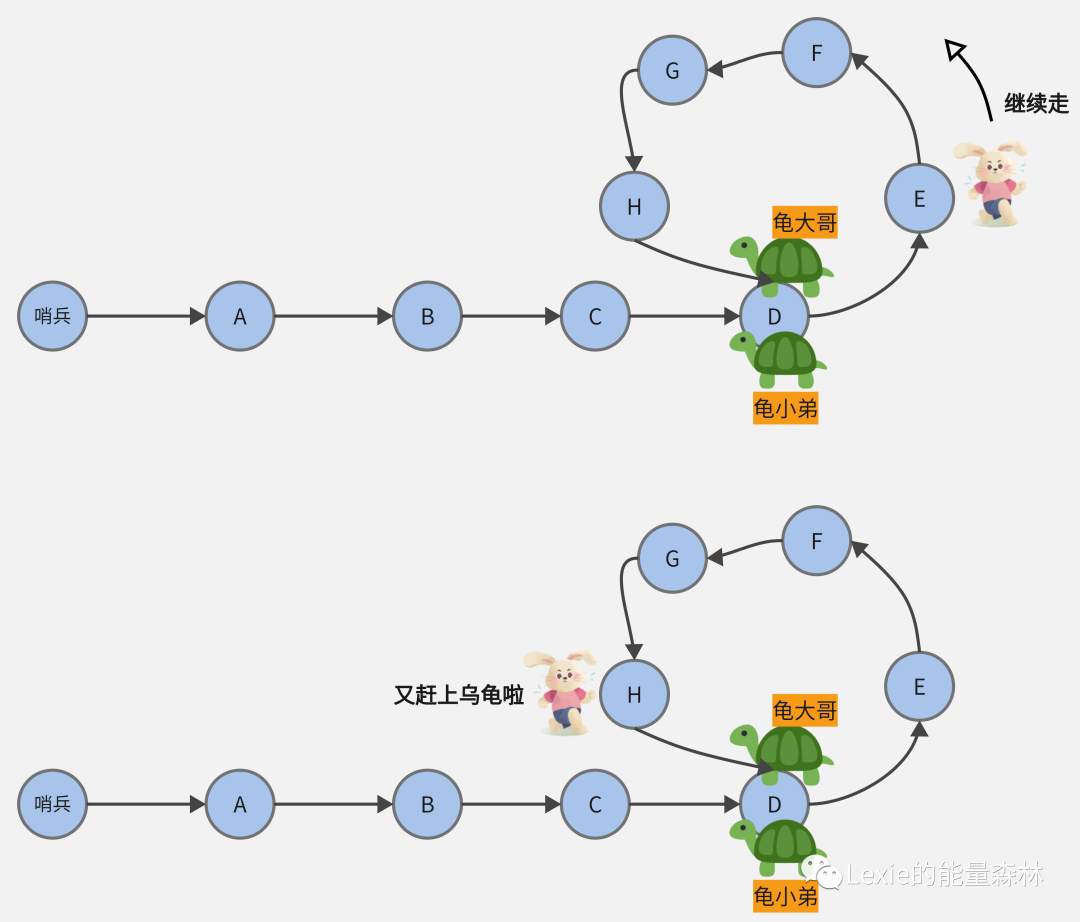
环路的起点和终点都明确了,将起点和终点间的链接断开,则环路断开,问题解决!
原理说完了,来看看用python代码如何实现吧。
class Cell:
"""定义链表节点类"""
def __init__(self, value, next):
self.value = value
self.next = next
def __str__(self):
return f"{self.value}"
def has_loop_tortoise_and_hare(sentinel):
"""
输入是链表的哨兵节点
存在环路返回True,并断开环路
"""
# 乌龟从哨兵节点出发,兔子从第一个节点出发
# 简化边界条件,不影响环路判断
tortoise = sentinel
hare = sentinel.next
while tortoise != hare:
# 当兔子到达链表末尾时,不存在环路.
# 由于兔子每次移动两个节点,所以需要判断当前和下一个节点
if (hare == None) or (hare.next == None):
return False
# 乌龟每步移动1个节点,兔子每步移动2个节点.
tortoise = tortoise.next
hare = hare.next.next
# 兔子和乌龟相遇后,第二只乌龟从哨兵节点出发
# 第一只乌龟从相遇后下一个节点出发,抵消一开始比兔子多走的一步
new_tortoise = sentinel
tortoise = tortoise.next
while tortoise != new_tortoise:
tortoise = tortoise.next
new_tortoise = new_tortoise.next
# 两只乌龟在环路起点相遇,兔子开始每次移动一个节点,寻找环路终点
while hare.next != tortoise:
hare = hare.next
# 断开环路
hare.next = None
# 存在环路
return True
算法复杂度分析
兔子和乌龟本质就是快慢指针。由于慢指针最多走一遍单链表,所以该算法是线性级时间复杂度 O(n);
程序只需保存几个指针,还有环路的起点、终点,所以空间复杂度为 O(1),是常数空间的算法。
参考文献
《算法基础:python 和 C#实现》罗德·斯蒂芬斯 著,余青宋 江红 余靖 译






