前言
张量（tensor）这个词听得多了，但总不知所云，不妨学习一下，从向量空间开始，讲一些前期储备，到张量具体定义为止，不求甚解，提供了一些向量空间中和物理比较相关的概念、张量的一个初步印象，后面可能会继续补充一些，积累数学储备不能被数学束缚，学我所需，来去自如~
本文主要为Jeevanjee的教材、Arfken写的Mathematical Methods For Physicists的读书记录。如果你在我的公众号文章中看到某本教材，大概率我是有电子版的（某些书异常罕见，占用了我不少精力和开支，当然和知识比起来不值一提），如需要可以在后台留言，我看到后会发给你用来学习。
顺带一提为了稍微严谨一点本文标题可以加一个“域上的”，区别于“环”、“模”什么的，忽略即可。张量有很多定义方式，多重线性函数的定义方式是比较正规和容易理解的，本文不需要太多的储备，简单的线性代数学过足矣。
1 向量空间
1.1 定义
一个抽象向量空间由以下几部分组成：
[1] 一个元素称为向量的集合V
[2] 一个元素为标量的集合C（一般是或）
[3] 对加法和标量乘法是封闭的，满足以下公理：
向量空间的标量乘法依赖于C，当需要指明时，我们说V是C上的向量空间，上的向量空间称为实向量空间，上的向量空间称为复向量空间。
张成（span）：是中k个向量的集合，则Span 或者Span S定义为具有以下形式的向量的集合：
也就是我们熟悉的的线性组合。
向量空间的基就是一组可以张成的一组有序的线性无关的向量集合。这里的“有序”强调了如果有一组有相同向量但顺序不同的向量集，则这两个基是不同的。有限基中向量的个数即为有限维向量空间的维数。
1.2 一些例子
例如，是我们熟悉的三维笛卡尔空间，是狭义相对论中的时空，在经典物理中常用来描述多粒子系统的位形空间。向量的定义是广义的，例如在一定区间平方可积的复值函数构成一个复向量空间，这里函数也是向量，事实上，下文会提到，的基是，是无限维的，是一个无限维希尔伯特空间（Hilbert space）。
狭义上的向量只是一维矩阵（行向量、列向量），但在这里，容易从上述定义发现矩阵属于广义向量。向量空间有实向量空间和复向量空间之分，构成向量的元素是实数还是复数不是判断向量属于实向量空间还是复向量空间的依据，关键是看标量乘法中的c对实数成立还是复数成立，例如所有的厄密矩阵（转置共轭等于自身的矩阵）当被虚数i作用时，成为反厄密矩阵，不满足封闭性，尽管厄密矩阵非对角元可以是复数，所有的厄密矩阵构成一个实向量空间。 对于定义中的标量集C的元素为复数的复平面（complex plane）是可以由1张成，因为，因此是一维的，对于定义中的标量集中元素为实数的复平面，记为，因为，因此是二维的。因此尽管向量集合、是一样的，但是因为标量集的不同而既可以是一维，也可以是二维，我们称为复数一维的（复向量空间）、实数二维的（实向量空间）。当我们在谈论复平面时，实际上更多是在讨论而不是。
1.3 分量（Components）
由于有基，向量空间的任何向量都可以用基进行展开：
我们称这些是相对于的分量。进一步的，我们可以把向量用行向量（基是行向量）或者列向量（基是列向量）来表达：
向量独立于任意选择的基而存在，但是例如写成的行向量或者列向量的的表达式依赖于基的选择，不同的基有不同的展开，所以对应的分量、行向量或列向量是不同的。 按照基的展开：
上式其实就是典型的的傅里叶级数，而就是傅立叶系数，同时也是相对于的分量。
1.4 线性算子（Linear Operators）
向量空间的一个线性算子是一个从映射到自身的线性函数（线性变换）：
我们有时把写作。上所有线性算子的集合构成一个空间，记为。的实矩阵就是上按照矩阵乘法作用的线性算子。因此或可以看成元素本身是线性算子的向量空间。在一个空间，我们定义一个线性算子以该方式作用于（对易子，commutator）：
上式中在上的作用称为伴随作用（adjoint action），或者称为伴随表示（adjoint representation）。 线性算子和矩阵是不同的东西。在一个有限维向量空间，选择基，那么线性算子的作用可以由它在基上的作用决定：
称为向量相对于基的分量，注意到，即的第j个分量，我们有：
这看起来像矩阵，事实上，我们我们可以定义在基上的矩阵，记为：
当写成上式时，的作用变成矩阵的乘法作用，此外，如果我们有两个线性算子、，我们定义其乘积（product）或复合（composition）为线性算子：
。算子的分量成为了相应的矩阵。
1.5 对偶空间（Dual Spaces）
粗略地说，一个对偶向量是一个“吃掉”一个向量并“吐出”一个数的对象。准确地说，对于一个给定的向量空间和标量集，上的一个对偶向量（或说线性泛函（linear functional））是上一个值属于标量集的线性函数（C -valued linear function），同样线性意味着：
注意到和是标量，将向量映射为标量，将向量的加法映射为标量的加法。上对偶向量的集合称为的对偶空间，并记为，是标量集上的向量空间。 举个例子。设为的一个基，因此任意的向量可以写为，所以我们可以通过以下方式定义一个对偶向量：
也就是把视为的第i个分量。显然，满足：
对偶向量的一个关键性质是它完全由其作用在基向量上的值决定，根据线性性质，我们有：
我们定义了。
如果是有限维的，维数为n，那么容易检验（两边同时作用于基向量）：
从上式可以看出为在上的分量。因为是任意的，这意味着张成，利用容易证明是线性无关的，因此就是对偶空间的基，我们有时称是的对偶。注意到和具有相同的维度。我们可以相对于基将写成分量的形式：
借助于行向量我们可以把写为：
在不引起歧义的情况下，上式最后一个等式去掉了表示基的下标。
在有限维，我们看到中的基诱导了中的基，但这在无限维并不是这样，在无限维，我们仍然有给定基的线性泛函，但这些线性泛函并不张成对偶空间。考虑，我们定义为：
这一定义满足，因此是的对偶。但是有些线性泛函并不能写成的线性组合，其中之一为狄拉克δ函数：
2 张量
张量的三个重要属性
(1) 秩：A function which eats a certain number of vectors (known as the rank r of the tensor) and produces a number.
(2) 多重线性：The distinguishing characteristic of a tensor is a special property called multilinearity, which means that it must be linear in each of its r arguments.
(3) 分量：These values of the function on basis vectors are nothing but the familiar components of the tensor
—An Introduction to Tensors and Group Theory for Physicists
2.1 初识张量
2.1.1 列维—奇维塔（Levi–Civita）
按照前面提到的张量的属性，我们不妨尝试设计一个rank-3 张量，在设计的过程中理解张量是什么。设"吃掉"了三个向量u、v、w（我在下文称其为（有序）基组，即基向量的有序组合），并产生了一个新的数，并且我们把设定为u、v、w张成的（有方向的）平行六面体的体积，我们能导出该体积为
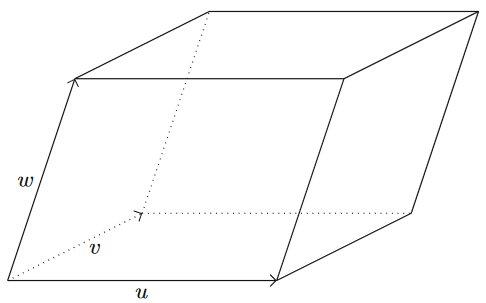
为了让确实成为一个张量，必须要是多重线性（multilinear）的，这意味着：
可以验证满足上式
如果取u、v、w为基向量，，可以推出：
按照上面的设定，我们可以定义张量的分量（components）为，而这正是物理中常见的Levi–Civita符号。
事实上，我们上面设计的张量被称为体积张量（volume tensor）或Levi–Civita张量（Levi–Civita tensor），当基组以组合时，Levi–Civita符号对应的就是Levi–Civita张量的分量，张量的分量就是给定一组基向量计算得到的张量的值，在几何上，对应的是张成的（有方向的）平行六面体的体积。
在最开始定义时，我们并没有指定u是什么，v是什么，w是什么，代表平行六面体体积这一特性不随基组的选择而变化，张量独立于任何基向量存在，但其分量却是依赖基组的。
2.1.2 rank-2 张量
下面的讨论中，我们会认识到一个张量就是一个多重线性函数（multilinear function）。我们考虑rank-2 张量T，“吃掉”两个向量v、w，并产生一个数T(v,w)，前面提到，多重线性意味着：
多重线性带来一个重要的性质，如果我们用向量空间的坐标基底如来表示基向量，即：
那么我们能够得到
我们定义：
则：
上式再次表明给定一组基向量，张量的分量就是张量的函数值。假定我们有一组新的基底向量，，与旧基底的关系是：
我们重新计算张量的分量，例如：
之后我们会学习到，采用爱因斯坦求和约定（Einstein summation convention），可以把上式写为：
张量可以用矩阵描述，但不是矩阵，当我们把分量写成矩阵形式[T]：
则T(v,w)可以写为：
需要注意的是，这种张量与矩阵的关系依赖于基的选择，且写成矩阵形式[T]只是为了方便计算。T是一个多重线性函数，而[T]是T在特定坐标系统中的表象（representation）。 过去，矩阵、张量通常被视为将向量转化为向量的线性算子（算符），但我们这里张量的定义是“吃掉”向量，“吐”出数字。其实，对于rank-2 张量，这两种观点是等同的。假设我们有一个线性算子R，我们可以通过下式将R转化为rank-2 张量：
上式可以粗略理解为把v、w“吃掉”，并“吐出”Rw在向量v方向上的分量。
计算的分量，例如：
我们发现张量的分量和线性算子的分量相等，具体的：
这个例子告诉，我们可以向三明治一样将线性算子R夹在两个向量中间得到一个rank-2 张量。反过来，我们也可以将一个二阶张量T转化为一个线性算子：
这建立了rank-2 张量与线性算子之间的一一对应关系，两者因此等价。
现在我们研究一下rank-2 转动惯量张量，角速度为，角动量为，动能为（kinetic energy），取基底为，我们可以认为是由下式定义的rank-2 张量：
2.1.3 rank n
事实上，标量是rank 0张量（0个基向量），向量是rank 1张量（1个基向量），rank n张量在d-维空间（d-dimensional space）中是一个具有以下特性的对象：
[1] 具有由n个指标标注的分量，每个指标可以从1到d中取，因此一共有个分量。
[2] 分量在特定的坐标变换下按照特定的方式变换。这是很重要的，因为物理量本质上不能因为坐标系统的选择而变化。
我们这里对张量随着基的变换的变换没有太多讨论，这并不影响我们导出张量的定义，但对理解张量特别重要，我可能会在后面的文章中学习分享。
2.2 更进一步的定义
2.2.1 爱因斯坦求和约定（Einstein Summation Convention）
当表达式中一个指标同时出现上标和下标时，省略对该指标的求和符号，这样变为，变为，被求和的指标称为哑标（dummy index），如这里的，未被求和的指标被称为自由标（free index），如这里的。在写任意基或坐标下的方程时，自由标只能在等式两边各出现一次，且在相同的位置（同时在上方或下方）。 当然爱因斯坦求和约定不止这些内容，其他的约定涉及更多概念时再引进即可。
2.2.2 定义
前文，我们把rank n的张量定义为一个“吃掉”n个向量并产生一个数的多重线性函数，现在我们推广一下这个定义，一个张量“吃掉”r个向量和s个对偶向量（dual vectors），我们定义在向量空间V（r,s）型张量为一个C值函数（C -valued function，C是指标量集）T：
对于每个变量（argument）满足线性，即多重线性，例如：
可以把对偶向量视为(1,0)型张量。向量视为(0,1)型张量，如下：
线性算子可以被视为(1,1)型张量：
向量是(0,1)型张量、线性算子是(1,1)型张量并不是那么显然的，不过可以从上文中的讨论里直觉上感受这一观念。
标量可以视为(0,0)型张量。
向量空间上(r,s)型张量，记为或，形成一个向量空间，前文我们看到：
利用爱因斯坦求和约定，上式可以写为，类似的，利用多重线性，我们有：
为张量相对于基的分量：
[1]
JEEVANJEE N. An Introduction to Tensors and Group Theory for Physicists[M]. Cham: Springer International Publishing, 2015.[2] ARFKEN G B, WEBER H J, HARRIS F E. Mathematical Methods for Physicists: A Comprehensive Guide[M]. 7th edition. Amsterdam ; Boston: Academic Press, 2012.
