Turro 1_分子光化学范式

1 光化学、光物理及范式

⭐️The field of molecular organic photochemistry can be conveniently classified in terms of the photophysics of organic compounds and the photochemistry of organic compounds. —Turro

广义上的分子光化学包括光化学与光物理，尽管光物理过程并没有发生净的化学反应，但要理解光化学反应，就必须理解光物理过程。事实上，光化学过程与光物理过程存在竞争关系。下面一个简单的方程概括了分子有机光化学的全过程：R+hv→∗R→P

有机分子（R）吸收光子（hv）成为激发态分子（*R）并最终形成产物（P），如果P=R，则为光物理过程，如果P≠R，则为光化学过程。

像上面这样简单的一个式子称为一个“范式”（paradigm），该词最早由Thomas Kuhn定义。

Paradigm: a complex set of intellectual experimental structures consisting of assumptions, concepts, strategies, methods, and techniques that provide a framework for performing scientific research in a field and for organizing and interpreting observable phenomena of the universe in a systematic and organized manner.

Turro在Molecular Photochemistry of Organic Compounds一书中通过有详有略的范式为学习分子光化学提供了框架。

我们不知不觉就在使用范式，与套模板类似，但可以上升为方法论，范式一般有成熟的实验与理论基础，为我们提供了可靠的思路，发挥奥卡姆剃刀的作用。但是我们也要认识到范式不是一成不变的，主要原因有：实验信息的不完整性、理论的暂时性、新技术带来意外结果的必然性。如从经典力学到量子力学，我们将光子、电子理解为具有波粒二象性的量子实体（entity），这为非经典情况提供了更好的范式。

学习一个领域的范式的一个重要认知工具是对特定信息进行了清晰考虑并检验良好（well-tested）的样本（examples），称为范例（examplars）。如有机化学中的各种官能团就是各种范例。

上面的全局范式（global paradigm）概括性太强，我们需要一些工作范式（working paragm），下面进行一些范式的详细描述（补充）以形成工作范式。

2 第一次补充：中间过程

让我们补充一下对R+hv→∗R→P的描述：

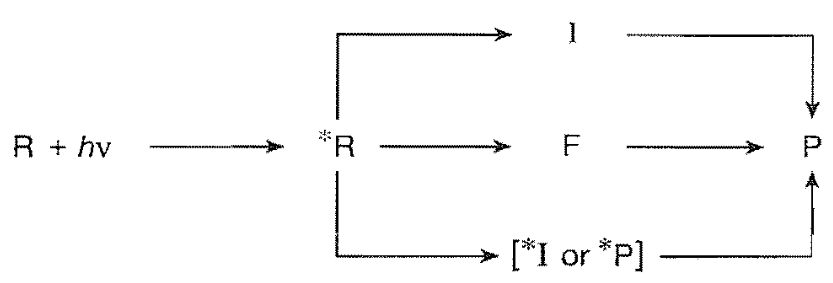
这里*R到P中间出现了三个选择，经过独立活性中间体（I，discrete reactive intermediate），漏斗（F，funnel），I的电子激发态或P的电子激发态（*I or *P），为简化起见，这里并没有显式地画出光物理过程。需要指出的是，这里的路径并不是独立和唯一的，比如可以*R→F→I→P，但I、F、*I、*P描述了所有的情形

①I：I可以为自由基对（RP，radical pair）、双自由基（BP，biradical）或两性离子（Z，zwitterion），是最常见的情形。自由基对是两个具有自由基中心的分子，双自由基是一个分子具有两个自由基中心（不要求定域）

②F：通过一个“漏斗”形成产物P，后面我们会用势能面的语言（锥面交叉，conical surface）来描述该过程③*I or *P：形成电子激发中间体（*I）或电子激发产物（*P），比较少见的情形

下图的例子（examples）中，（a）为经过自由基对的过程，（b）为经过双自由基的过程。k是反应速率常数。

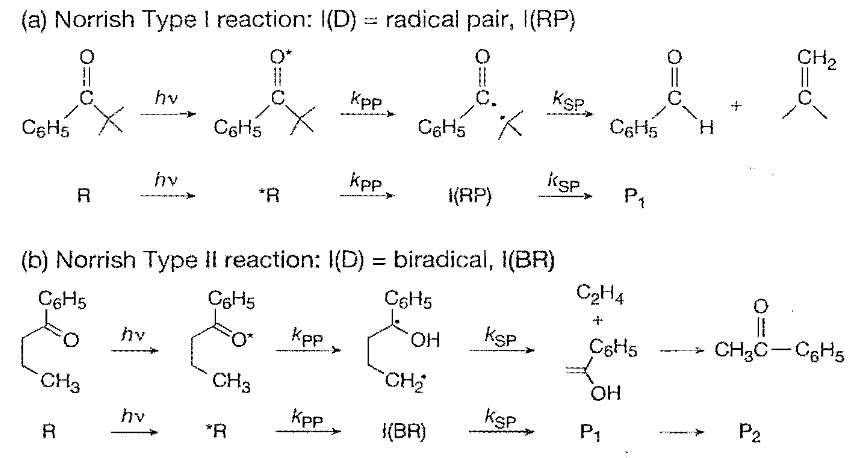
从*R到I的过程是初级光化学反应（primary photochemical reaction）过程，从I到P的过程（二级热反应（secondary thermal reactions））本质上与光化学反应无关（即使是热裂解形成的自由基，和光裂解形成的自由基在接下去的反应中行为是一样的），但是理解I→P的过程对理解整个光化学反应还是重要的。

3 第二次补充：分子轨道

我们讨论*R→I→P的路径。分子轨道理论认为，分子轨道由原子轨道线性组合得到，在前线分子轨道理论中，我们考虑两个前线分子轨道（MOs）——最高占据分子轨道（HOMO，简称为HO）、最低未占分子轨道（HUMO，简称为LU）。

如下图所示，在R与*R中，HO与LU的能带隙较大，基态分子（R）中HO上的一个电子吸收光子跃迁到LU上，成为激发态分子（*R）。这里并没有画出剩余的自旋成对的电子，这些能量较低的电子难以被扰动，对反应是次要的

中间体I拥有两个非键轨道（NB）（就是没有用于成键的轨道），它们的能量一般相近，两个电子处于两个NB上，如果这两个NB处于同一个分子中，对应的是双自由基（BP）；如果两个NB位于不同的分子，对应的是自由基对（RP），BP和RP都属于类双自由基（D，diradicaloid）。如果NB1和NB2的能量差有显著差距，则I中的两个电子倾向于到能量较低的那个轨道，形成两性离子Z(NB)²。

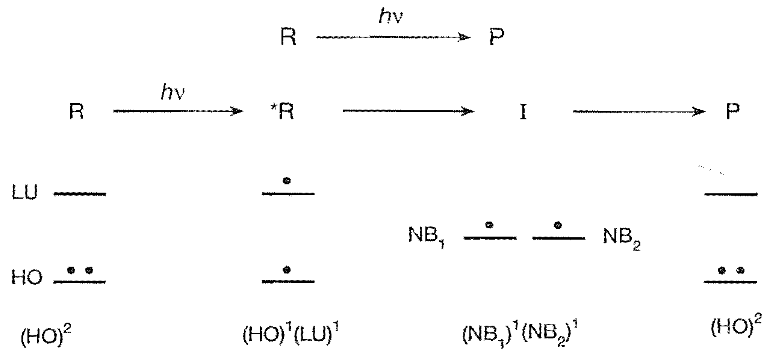
需要注意的是，当我们在利用分子轨道理论时，我们采用了单电子近似，忽略了电子激发后由于电子相互作用导致的轨道能量的变化

4 第三次补充：电子自旋

考虑电子自旋后，前面提到的激发态分为单线态（S）和三线态（T），电子的基态（S₀）总是单线态（自旋成对），而对于激发态，第一激发态、第二激发态等分别以S或T加上右下角标1，2，... 表示。在同一分子中，不同线态能态间的非辐射跃迁称为系间窜越（ISC，intersystem crossing），相同线态能态间的非辐射跃迁称为内转换（IC，ICinternal conversion）。非辐射跃迁指原子在不同能级跃迁时并不伴随光子的发射或吸收。不同线态能态间的辐射跃迁放出的光称为磷光，相同线态能态间的辐射跃迁放出的光称为荧光。

这里我们只画出了第一激发态，因为较高能量的激发态一般会快速失活回到S₁、T₁。

卡莎（kasha）规则：光子仅能由最低激发态以荧光或磷光的形式发射，因此发射光的波长与激发光的波长无关。当然有反例

如下图所示，考虑电子自旋后，*R分为单线态¹*R(S₁)和三线态³*R(T₁)，同样，I分为单线态¹*I(D)和三线态³*I(D)。

单线态、三线态的粗浅说法：电子自旋向上自旋磁量子数记为+1/2，自旋向下自旋磁量子数记为-1/2，两个电子组合后总自旋磁量子数s为0或1,而2s+1这个数是在标记原子状态时的一个记号罢了，在这里2s+1为0或3，分别记为单线态和三线态，当然更深的理解在量子力学中

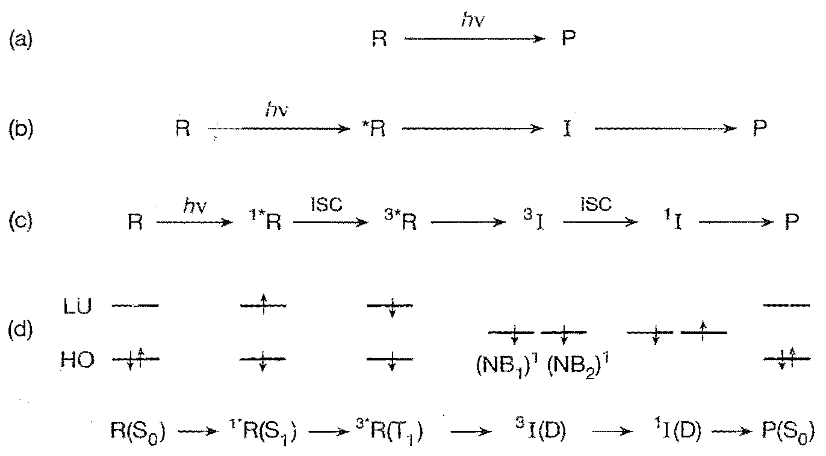
R与*R具有相同的组分（原子种类、数目）、相同构造（原子连接方式），但化学性质不同，我们称之为电子异构体，不同的电子构型产生电子异构体，不同的电子自旋组态产生自旋异构体，S_n与T_n间的关系称为自旋-电子异构体。

5 第四次补充：能态图

清晰了解反应过程中各分子状态的能量是重要的，我们以“能态图”来详细描述R(S₀)、*R(S₁)、*R(T₁)间的过程。在能态图中，y轴是系统的势能（PE，potential energy），x轴无特殊的物理意义。

从S₀到S₁的跃迁是自旋允许的（spin-allowed），从S₀到T₁的过程是自旋禁阻的（spin-forbidden），自旋禁阻的光谱强度仅为相应自旋允许的几百分之一。

从S₁到S₀可以通过辐射跃迁放出荧光，也可以通过非辐射跃迁进行内转换，能量以热能耗散，从S₁到¹I的过程称为单线态反应；从T₁到S₀可以通过辐射跃迁放出磷光，也可以通过非辐射跃迁进行系间窜越，从T₁到³I的过程称为三线态反应；S₁到T₁也是一种系间窜越。

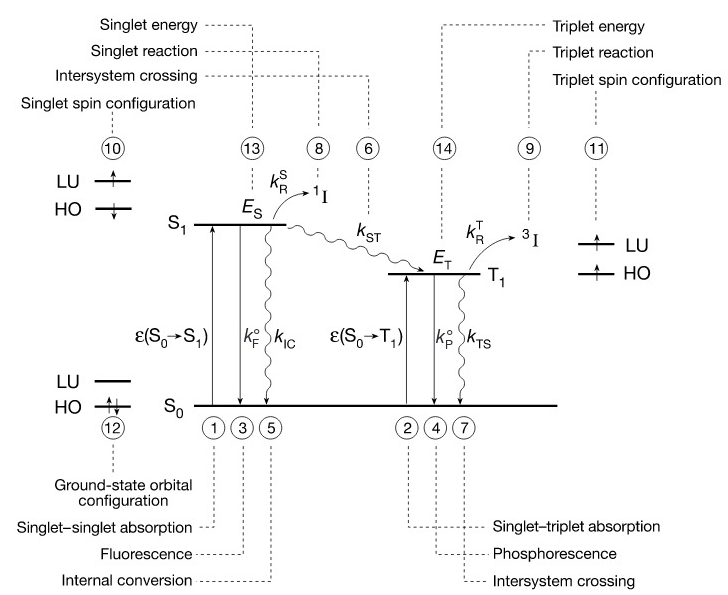
在之前我们提到过自旋-电子异构体，事实上，能态图上的能态间，有可能在电子构型和自选组态上都一致，但是原子核的分布是不一样的，这种情况叫做空间异构体。

⭐️非常重要的一点，在能态图中，我们假定核平衡态的几何构型是不变的，也就是假定R和*R的核几何构型是一样的，也就是电子跃迁后核的位置是不变的，但事实上，电子跃迁后核的几何构型会发生变化，核与电子相对位置的变化导致势能发生变化，下面我们将用势能面来重新描述激发态与基态之间的一些过程。

6 第五次补充：势能面

核的不同空间分布对应着不同的体系势能，如何在一张图上表示不同的空间分布然后对应不同的势能，显然我们要处理的是不计其数的核几何构型，这是高维的数学对象，但我们不妨把一个核几何构型视作x轴上的一点，x轴代表不同的核几何构型（分子结构），这就把高维问题转化为2D图（称为零级近似或工作近似），y轴仍然是势能。为简化起见，用能面来描述势能曲线。

沿着给定势能面的最低势能通道称为反应坐标。个人理解就是从一种核几何构型（如R）变化到另外一种核几何构型（如P），原子核位置分布需要调整，哪一系列调整对体系来说是势能上占优势的变化，一般来说，一种平衡的核几何构型是相应情况下势能最低的

势能曲线上每一个点代表不同的核几何构型（x）及相应的势能（y），对于一个给定的核几何构型（x），势能（y）主要由电子轨道构型及其自旋组态决定。当涉及多个势能面时，简化起见，假定从R开始的基态能面与从*R开始的激发态能面有相同的反应坐标。然而一般而言，对于R→P基态转换过程的最低能量路径并不需要与*R→P的最低能量路径相同，个人理解是由于一个点一次只能在一条曲线上，所以问题不大

两个势能面任意一点都可以作为（体系PE随核几何构型沿反应坐标变化的）代表点（representative point），光物理、光化学过程转化为代表点的运动（轨迹），代表点通过与环境中其他分子的碰撞沿反应坐标推进。

简单起见，下图对应的激发态为单线态。

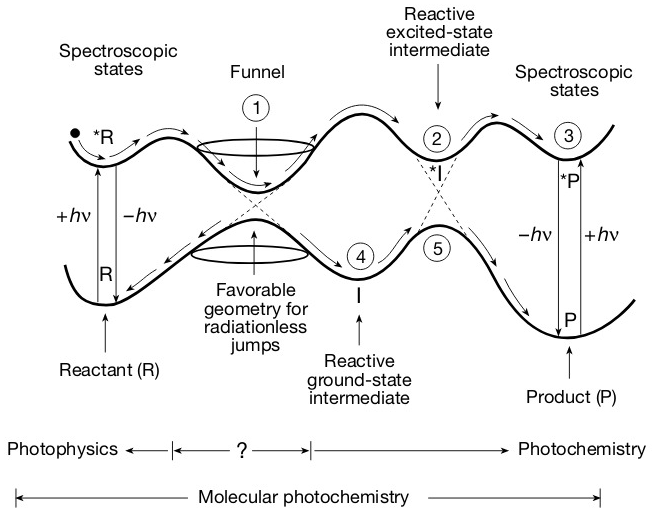
我们考虑一些假定的势能面的拓扑性质（定性的性质），如极值（较大值、极小值）、极值分布、两能面能差变化。

在R与*R间，吸收光子时从基态能面的极小值到激发态能面的极小值，发射光子时，从激发态能面的极小值到基态能面的极小值（也可以非辐射跃迁从*R到R），这种极小值称为光谱（Franck-Condon极小值），由于沿着反应坐标的推进有小的能垒（几kcal/mol），因此类似于势阱效应，这种过程比较容易发生。我们看到R与*R附近的势能曲线变化趋势是相似的，意味着基态与激发态的核几何构型相似，事实上，相对于振动，吸收光子后从R到*R的电子跃迁非常快，导致核的几何构型来不及变化就发生了，发生“垂直跃迁”。

弗兰克-康登原理：在发生电子跃迁时，分子中各原子核的位置及其环境可视为几乎不变。

电子激发态的代表点在*R→P的过程中，沿着激发态能面推进，当遇到漏斗（funnel）时，可在很短时间时间内从一能面跳跃到另一能面，对单线态而言，跳跃的时间非常短。漏斗对应着激发态能面的极小值与基态能面的极大值，描述为势能面交叉，包括真实的交叉、弱避免交叉（weakly avoided crossings，图中区域①）、强避免交叉（strongly avoided crossings，图中区域②）

事实上，基态能面的极大值都可以近似看做一个交叉区域，上图中弱避免交叉对应的是基态能面上一个较大的能垒，强避免交叉对应的是基态能面上一个较小的能垒。

电子跳跃后新电子分布产生的新负电力场导致分子的原子核重排以适应新的电力分布，核运动产生核动能（这种情况下产生的核动能称为振动能），（在几皮秒内）能量迅速通过分子内、分子间转移至周围溶剂，使*R达到最小振动能。代表点的运动控制这核的运动，在漏斗处，两能面接近，相互竞争代表点，核体系的控制权被打乱。

在*R以非辐射路径向P推进的过程中，归因于与周围分子的热碰撞，*R上的代表点克服小的能垒沿激发能面推进到区域①，弱避免交叉促进从激发能面到基态能面的跳跃，跳跃后，很可能“摔落“回R，这是光物理过程。极少数情况下，*R获得足够的热能继续在激发态能面推进，到达电子激发态活性中间体（*I），这时候，光化学过程就发生了。在一些罕见的情况下，代表点从*I沿激发态能面推进到*P，然后最终形成P，这种路径成为绝热光反应（adiabatic photoreaction），可能（possible）发生，但是除了特殊条件下并不是（似乎）合适（plausible）的路径。

从以上讨论我们可以看出，光化学过程和光物理过程是竞争的。

7 寻找最佳可能路径

现在我们了解到从底物（R）到产物（P）有许多路径，那么究竟那一条才是最佳可能路径呢？一个比较好的思路就是，在给定条件下，先列出所有可能的（possible）路径，在这一过程中，随便我们异想天开。然后通过一些约束条件进行选择。主要的约束（选择规则）有：

①四个化学反应守恒定律：能量守恒、动量守恒（线动量、角动量）、质量守恒（原子种类与数目）、电荷守恒。②就是我们接触到的范式。当然如果合理我们可以跳出范式提出新思路并进行检验

进行初步的选择规则，我们完成了从可能到（似乎）合适（plausible）的过渡，从合适到最佳可能（probable），我们需要进一步的选择规则，进行动力学计算或实验，算出或测定各条路径的速率常数，在合适的基础上，这时最快的一条路径往往就是最佳可能路径。

当你耐心读完，你会发现只在Turro的第一章（绪论）的前半部分里，竟然有那么多好玩的东西，全书一共一千多页，我们的旅程刚刚开始
🚀

[1] TURRO N J, RAMAMURTHY V, SCAIANO J C. Modern molecular photochemistry of organic molecules[M]. University Science Books Sausalito, CA, 2010, 188.

• 本文一些叙述如有错误，请联系指出，感谢🌸