
● 以下内容授权自 傅志凌(华东理工大学队员)解析C/C++A组题目:
https://blog.csdn.net/fzl194/article/details/124347039
傅志凌是http://oj.ecustacm.cn的所有者和管理员
2022年蓝桥杯省赛 C/C++ A组题解
前言: NewOJ最新推出2022蓝桥杯省赛题目,数据均为管理员自行构造,仅供参考。
传送门:http://oj.ecustacm.cn/viewnews.php?id=1021。
题目总览
题目 | Tag | 难度 | 补题链接 |
裁纸刀 | 模拟 | ☆ | http://oj.ecustacm.cn/problem.php?id=2021 |
灭鼠先锋 | 博弈 | ☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2022 |
求和 | 前缀和 | ☆☆ | http://oj.ecustacm.cn/problem.php?id=2023 |
选数异或 | 线段树、S T表 | ☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2024 |
爬树的甲壳虫 | 期望DP 、逆元 | ☆☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2025 |
青蛙过河 | 二分答案、贪心 | ☆☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2026 |
最长不下降子序列 | 动态规划、线段树 | ☆☆☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2027 |
扫描游戏 | 计算几何、线段树 | ☆☆☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2028 |
数的拆分 | 数论 | ☆☆☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2029 |
推导部分和 | 并查集、搜索 | ☆☆☆☆ | http://oj.ecustacm.cn/problem.php?id=2030 |
注:本次C++ A组的题目题目质量很好,但是难度过大,线段树考点重复(也可能存在其他做法)。
试题A:裁纸刀

Tag:模拟
难度:☆
试题B:灭鼠先锋
XOOO XXOO OXOO OXXOOOOO OOOO OOOO OOOO
Tag:博弈
难度:☆☆☆
思路:博弈题核心:
只能转移到必胜态的,均为必败态。
可以转移到必败态的,均为必胜态。
1.首先确定最终的必败态:只剩下1个棋子的时候肯定是必败的。
2.利用上述提到的核心,倒推出其他情况属于必败态还是必胜态。
OXXX XOXXXXXX XXXX
3.注意,给定的4个局面为先手第一步的四种局面,对于此时局面为必胜态,表示的是后手胜。
#include<bits/stdc++.h>using namespace std;///判断是否仅存在一个空格bool check(string s){int tot = 0;for(auto x : s)if(x == 'O')tot++;return tot == 1;}map<string, bool>SG;bool dfs(string s){if(SG.count(s))return SG[s];if(check(s))return SG[s] = false;模拟放1个棋子for(int i = 0; i < s.size(); i++)if(s[i] == 'O'){string tmp = s;tmp[i] = 'X';if(dfs(tmp) == false)///可以到达必败态均为必胜态return SG[s] = true;}模拟放2个棋子for(int i = 0; i < s.size() - 1; i++)if(s[i] == 'O' && s[i + 1] == 'O' && i != 3){string tmp = s;tmp[i] = tmp[i + 1] = 'X';if(dfs(tmp) == false)///可以到达必败态均为必胜态return SG[s] = true;}运行到此,说明只能转移到必胜态,此时为必败态return SG[s] = false;}int main(){string s[] = {"XOOOOOOO", "XXOOOOOO", "OXOOOOOO", "OXXOOOOO"};for(int i = 0; i < 4; i++){if(dfs(s[i]))cout<<"L";///此时为必胜态,说明后手面临的局面必胜,输出Lelse cout<<"V";}return 0;}
题意: 给定数组,求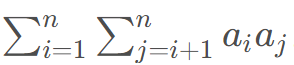 。
。
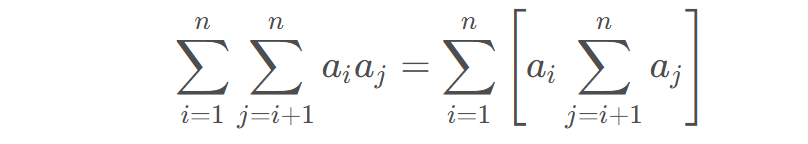
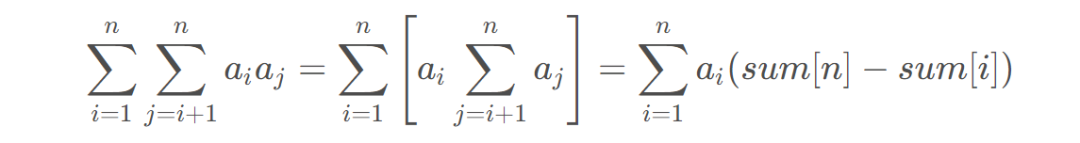
预处理前缀和即可,时间复杂度O(n)。
#include<bits/stdc++.h>using namespace std;typedef long long ll;const int maxn = 2e5 + 10;ll a[maxn], sum[maxn];int main(){int n;ll ans = 0;cin >> n;for(int i = 1; i <= n; i++) ///预处理前缀和cin >> a[i], sum[i] = sum[i - 1] + a[i];for(int i = 1; i <= n; i++) ///求和即可ans += a[i] * (sum[n] - sum[i]);cout<<ans<<endl;return 0;}
试题D:选数异或
题意:给定数组a和整数x,m次询问,每次询问区间[l ,r ]是否存在两个数字使得异或值等于x。
Tag:线段树、ST表
难度:☆☆☆
思路:由于给定x,对于区间[l ,r ]中的每个数字a [ i ] 而言,只需要判断区间[l ,r ]中是否存在 。
。
暴力判断会超时,如何快速判断区间[l ,r ]而不是一个一个a [ i ] 来判断?
对每个数字a [ i ] ,找到它左边最近的a [ j ] ,满足 ,则<j , i > 二元组是一个合法解,其中j <i 。
,则<j , i > 二元组是一个合法解,其中j <i 。
为什么一定是左边最近合法位置而不是右边最近?
二者是一样的,因为i找到的左边最近合法位置是j ,j 找到的右边最近是i 。
对于每个i,都找到左边最近合法的j,记为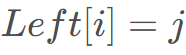 ,满足
,满足 。
。
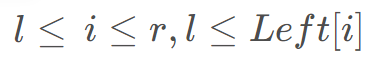 。
。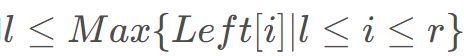 。
。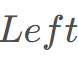 数组?从左往右遍历时,利用pos [x ] 记录数字x 上一次出现的位置,那么
数组?从左往右遍历时,利用pos [x ] 记录数字x 上一次出现的位置,那么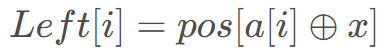 。
。#include<bits/stdc++.h>using namespace std;const int maxn = 100000 + 10;int tree[maxn << 2];int Left[maxn], pos[(1 << 20) + 10];int a[maxn], n, m, x;//线段树模板void build(int o, int l, int r){if(l == r){tree[o] = Left[l];return;}int mid = (l + r) >> 1;build(o << 1, l, mid);build(o << 1 | 1, mid + 1, r);tree[o] = max(tree[o << 1], tree[o << 1 | 1]);}int query(int o, int l, int r, int L, int R){if(L <= l && r <= R)return tree[o];int mid = (l + r) >> 1;int ans = 0;if(L <= mid)ans = max(ans, query(o << 1, l, mid, L, R));if(R > mid)ans = max(ans, query(o << 1 | 1, mid + 1, r, L, R));return ans;}int main(){scanf("%d%d%d", &n, &m, &x);for(int i = 1; i <= n; i++) //预处理Left数组{scanf("%d", &a[i]);Left[i] = pos[a[i] ^ x];pos[a[i]] = i;}build(1, 1, n);//线段树建树while(m--){int l, r;scanf("%d%d", &l, &r);if(query(1, 1, n, l, r) >= l)//查询区间最值printf("yes\n");elseprintf("no\n");}return 0;}
试题E:爬树的甲壳虫
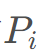 的概率会掉回树根,求它从树根爬到树顶时,经过的时间的期望值是多少。
的概率会掉回树根,求它从树根爬到树顶时,经过的时间的期望值是多少。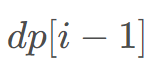 表示从高度i -1出发到顶部花费的期望时间。根据题意可以得到如下的状态转移方程:
表示从高度i -1出发到顶部花费的期望时间。根据题意可以得到如下的状态转移方程: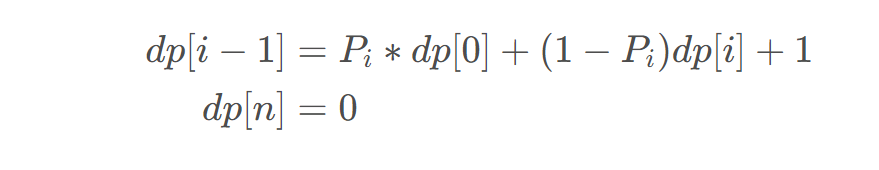
利用递推式展开:
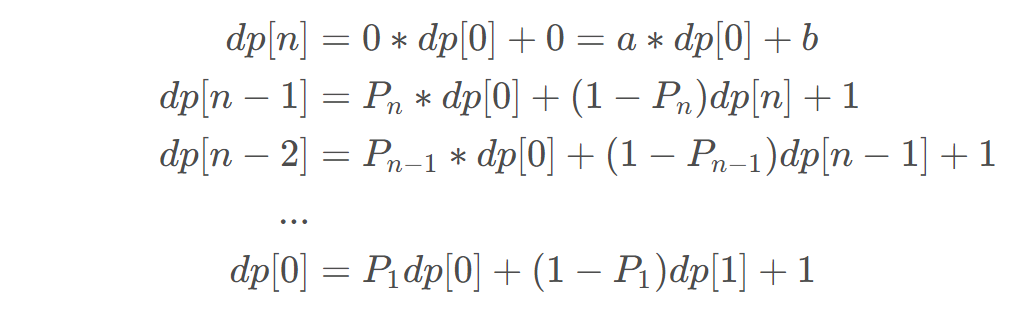
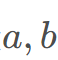 ,分别表示
,分别表示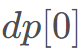 的系数和常数,初始均为0。
的系数和常数,初始均为0。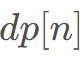 代入
代入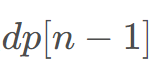 中,得到新的
中,得到新的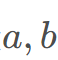 :
: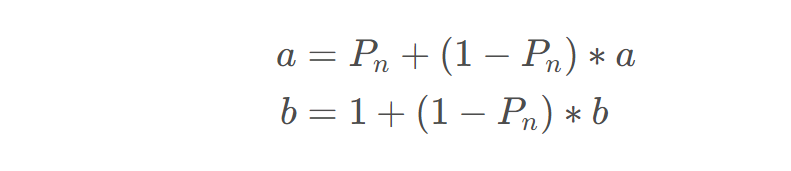
最终可以得到:
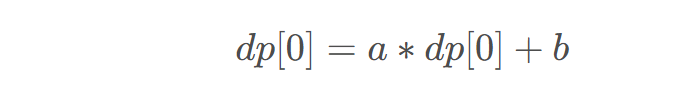
遍历中全部使用模意义下的数字,求解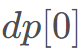 的时候相当于求解:
的时候相当于求解:
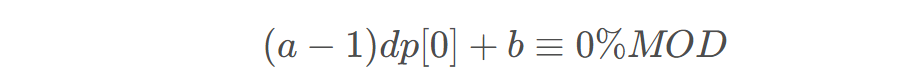
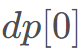 即可。
即可。#include<bits/stdc++.h>using namespace std;typedef long long ll;const int maxn = 1e5 + 10;const int MOD = 998244353;ll x[maxn], y[maxn];ll ksm(ll a, ll b, ll m){ll ans = 1;while(b){if(b & 1)ans = ans * a % m;b >>= 1;a = a * a % m;}return ans;}ll inv(ll x){return ksm(x, MOD - 2, MOD);}ll extgcd(ll a, ll b, ll&x, ll&y)//ax+by = gcd(a, b)的解。返回值为gcd{ll d = a;if(b){d = extgcd(b, a % b, y, x);y -= (a b) * x;}else x = 1, y = 0;return d;}int main(){int n;cin >> n;for(int i = 1; i <= n; i++){cin >> x[i] >> y[i];ll g = __gcd(x[i], y[i]);x[i] = x[i] g;y[i] = y[i] g;}ll a = 0, b = 0;for(int i = n; i >= 1; i--){ll p = x[i] * inv(y[i]) % MOD, p_1 = (y[i] - x[i]) * inv(y[i]) % MOD;a = (p + p_1 * a) % MOD;b = (1 + p_1 * b) % MOD;}///cout<<x[1]<<" "<<y[1]<<" "<<inv(y[1])<<endl;///dp[0] = a * dp[0] + b///(a-1)dp[0]+k * MOD = MOD - b///(a - 1)x + MOD * y = MOD - b///cout<<a<<" "<<b<<endl;ll c = a - 1, d = MOD, x, y;ll g = extgcd(c, d, x, y);///cout<<x<<" "<<y<<endl;ll x1 = x * (MOD - b) g;ll y1 = y * (MOD - b) g;cout<<(x1 % MOD + MOD ) % MOD<<endl;return 0;}
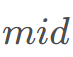 ,一种思想是每次能跳多远跳多远,然后去模拟判断
,一种思想是每次能跳多远跳多远,然后去模拟判断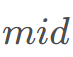 是否合法,做法比较复杂,暂不展开。
是否合法,做法比较复杂,暂不展开。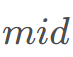 的区间之和是否大于等于2x ,如果每个区间和都大于2x ,肯定可以保证构造出一组解通过2x 次。反过来是否成立可以自行思考一下。
的区间之和是否大于等于2x ,如果每个区间和都大于2x ,肯定可以保证构造出一组解通过2x 次。反过来是否成立可以自行思考一下。#include<bits/stdc++.h>using namespace std;const int maxn = 1e5 + 10;template <typename T>inline T read(T& x) {x = 0;T w = 1;char ch = 0;while (ch < '0' || ch > '9') {if (ch == '-') w = -1;ch = getchar();}while (ch >= '0' && ch <= '9') {x = x * 10 + (ch - '0');ch = getchar();}return x * w;}int h[maxn], sum[maxn];int n, x;//判断所有长度为mid的区间之和是否大于等于2xbool check(int mid){for(int i = 1; i + mid - 1 <= n; i++)if(sum[i + mid - 1] - sum[i - 1] < 2 * x)return false;return true;}int main(){read(n); read(x);for(int i = 1; i <= n - 1; i++)//预处理前缀和read(h[i]), sum[i] = sum[i - 1] + h[i];sum[n] = 1e9 + 7;int left = 1, right = n, ans = n;while(left <= right)//二分答案{int mid = (left + right) >> 1;if(check(mid))ans = mid, right = mid - 1;//求最小合法解elseleft = mid + 1;}cout<<ans<<endl;return 0;}
题意:给定数组a ,可以修改连续的K 个数字变成一个相同值。请计算修改后的最长不下降子序列长度。
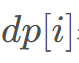 表示以
表示以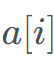 结尾的最长不下降子序列长度,对于修改连续的K 个数字变成同一值,最好修改成与前面一样的数字,即:
结尾的最长不下降子序列长度,对于修改连续的K 个数字变成同一值,最好修改成与前面一样的数字,即: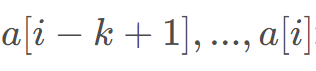 均修改成
均修改成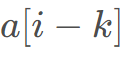 ,此时的最长上升子序列可以看成3段:
,此时的最长上升子序列可以看成3段:
为了求出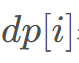 ,利用权值线段树求出
,利用权值线段树求出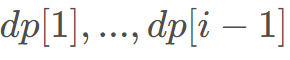 中最大的数字
中最大的数字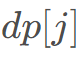 ,同时保证
,同时保证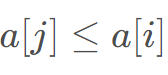 。
。
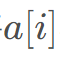 看作线段树的第
看作线段树的第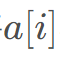 位,
位,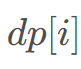 为线段树维护的值(线段树维护最大值),查询线段树区间
为线段树维护的值(线段树维护最大值),查询线段树区间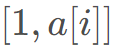 的最大值即可。
的最大值即可。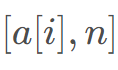 的最大值,就可以维护以x 开头的最长上升子序列,这样,最后暴力枚举每一段K 即可。
的最大值,就可以维护以x 开头的最长上升子序列,这样,最后暴力枚举每一段K 即可。#include<bits/stdc++.h>using namespace std;const int maxn = 1e5 + 10;template <typename T>inline T read(T& x) {x = 0;T w = 1;char ch = 0;while (ch < '0' || ch > '9') {if (ch == '-') w = -1;ch = getchar();}while (ch >= '0' && ch <= '9') {x = x * 10 + (ch - '0');ch = getchar();}return x * w;}int a[maxn], b[maxn];int dp[maxn];///dp[i]表示以i结尾的最长上升子序列///权值线段树,维护dp数组int tree[maxn << 2];void build(int o, int l, int r){tree[o] = 0;if(l == r)return;int mid = (l + r) >> 1;build(o << 1, l, mid);build(o << 1 | 1, mid + 1, r);}void update(int o, int l, int r, int x, int val){if(l == r){tree[o] = max(tree[o], val);return;}int mid = (l + r) >> 1;if(x <= mid)update(o << 1, l, mid, x, val);else update(o << 1 | 1, mid + 1, r, x, val);tree[o] = max(tree[o << 1], tree[o << 1 | 1]);}int query(int o, int l, int r, int L, int R){if(L <= l && r <= R)return tree[o];int mid = (l + r) >> 1;int ans = 0;if(L <= mid)ans = max(ans, query(o << 1, l, mid, L, R));if(R > mid)ans = max(ans, query(o << 1 | 1, mid + 1, r, L, R));return ans;}int main(){int n, k, tot = 0;read(n); read(k);for(int i = 1; i <= n; i++)read(a[i]), b[++tot] = a[i];if(n == k){cout<<n<<endl;return 0;}///离散化sort(b + 1, b + 1 + tot);tot = unique(b + 1, b + 1 + tot) - (b + 1);for(int i = 1; i <= n; i++)a[i] = lower_bound(b + 1, b + 1 + tot, a[i]) - b;build(1, 1, tot);int ans = 0;for(int i = 1; i <= n; i++)///从前往后遍历a,放入权值线段树中{///dp[i] = max(dp[j]) 满足j=1...i-1 && a[j] <= a[i]dp[i] = query(1, 1, tot, 1, a[i]) + 1;update(1, 1, tot, a[i], dp[i]);}///重新清空build(1, 1, tot);for(int i = n; i > k; i--)///从后往前遍历a,放入权值线段树中{///a[i-k+1] ... a[i]相等 均等于a[i-k]///最后一段要注意:查询的是[a[i-k],tot]中的最大值ans = max(ans, dp[i - k] + k - 1 + query(1, 1, tot, a[i - k], tot) + 1);int tmp = query(1, 1, tot, a[i], tot) + 1; ///以a[i]开始的最长上升子序列长度ans = max(ans, tmp + k);///插入的是a[i]update(1, 1, tot, a[i], tmp);}cout<<ans<<endl;return 0;}
题意:有一根围绕原点O 顺时针旋转的棒O A,初始时指向正上方(Y 轴正向)。在平面中有若干物件,第i个物件的坐标为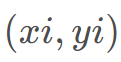 ,价值为
,价值为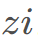 。当棒扫到某个物件时,棒的长度会瞬间增长z i zizi,且物件瞬间消失(棒的顶端恰好碰到物件也视为扫到),如果此时增长完的棒又额外碰到了其他物件,也按上述方式消去(它和上述那个点视为同时消失)。
。当棒扫到某个物件时,棒的长度会瞬间增长z i zizi,且物件瞬间消失(棒的顶端恰好碰到物件也视为扫到),如果此时增长完的棒又额外碰到了其他物件,也按上述方式消去(它和上述那个点视为同时消失)。
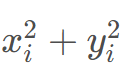 ,要找的是下一个小于等于
,要找的是下一个小于等于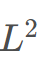 的点,因此维护最小值。
的点,因此维护最小值。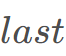 (初始为0),每次利用线段树查找区间
(初始为0),每次利用线段树查找区间 中从左往右第一个小于等于
中从左往右第一个小于等于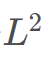 的数字,如果没有找到则查找区间
的数字,如果没有找到则查找区间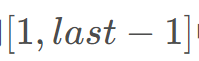 中从左往右第一个小于等于
中从左往右第一个小于等于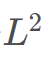 的数字(顺时针一圈)。
的数字(顺时针一圈)。 。棒长L 增加
。棒长L 增加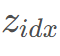 ,记录一下当前第
,记录一下当前第 个点的答案。注意特判一下,如果当前点和先前点夹角为0,则排名是一样的。
个点的答案。注意特判一下,如果当前点和先前点夹角为0,则排名是一样的。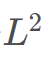 会超过
会超过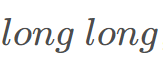 ,可以在代码中维护距离而不是距离的平方,也可以使用
,可以在代码中维护距离而不是距离的平方,也可以使用 来维护变量
来维护变量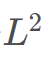 。
。#include<bits/stdc++.h>using namespace std;typedef long long ll;const int INF = 1e9 + 7;const int maxn = 2e5 + 10;template <typename T>inline T read(T& x) {x = 0;T w = 1;char ch = 0;while (ch < '0' || ch > '9') {if (ch == '-') w = -1;ch = getchar();}while (ch >= '0' && ch <= '9') {x = x * 10 + (ch - '0');ch = getchar();}return x = x * w;}struct point{ll x, y, z;int id;}a[maxn];ll n;__int128 L;int Quadrant(point a){if(a.x >= 0 && a.y > 0)return 1;///y的正半轴放到第一象限if(a.x > 0 && a.y <= 0)return 2;///x的正半轴放到第二象限if(a.x <= 0 && a.y < 0)return 3;return 4;}ll cross(point a, point b){return a.x * b.y - a.y * b.x;}bool cmp(point a, point b){if(Quadrant(a) == Quadrant(b)){if(cross(a, b) == 0)return a.x * a.x + a.y * a.y < b.x * b.x + b.y * b.y;elsereturn cross(a, b) < 0;}elsereturn Quadrant(a) < Quadrant(b);}__int128 mi[maxn << 2];void push_up(int o){mi[o] = min(mi[o << 1], mi[o << 1 | 1]);}void build(int o, int l, int r){if(l == r){mi[o] = a[l].x * a[l].x + a[l].y * a[l].y;return ;}int mid = (l + r) >> 1;build(o << 1, l, mid);build(o << 1 | 1, mid + 1, r);push_up(o);}void update(int o, int l, int r, int x, __int128 val){if(l == r){mi[o] = val;return;}int mid = (l + r) >> 1;if(x <= mid)update(o << 1, l, mid, x, val);else update(o << 1 | 1, mid + 1, r, x, val);push_up(o);}///找右边第一个小于等于z^2的数字ll idx;bool query(int o, int l, int r, int L, int R, __int128 z){if(L > R)return false;if(l == r){idx = l;return mi[o] <= z;}int mid = (l + r) >> 1;if(L <= mid){if((mi[o << 1] <= z) && query(o << 1, l, mid, L, R, z))return true;}if(R > mid){if((mi[o << 1 | 1] <= z) && query(o << 1 | 1, mid + 1, r, L, R, z))return true;}return false;}int ans[maxn];int main(){read(n);read(L);for(int i = 1; i <= n; i++){read(a[i].x);read(a[i].y);read(a[i].z);a[i].id = i;ans[i] = -1;}sort(a + 1, a + 1 + n, cmp);build(1, 1, n);int cnt = 0;int lastcnt = 0;int last = 0; ///上一个位置while(true){bool ok = query(1, 1, n, last + 1, n, L * L);if(ok)L = L + a[idx].z;else{ok = query(1, 1, n, 1, last - 1, L * L);if(ok)L = L + a[idx].z;else break;}update(1, 1, n, idx, 1e32);if(last){if(Quadrant(a[last]) == Quadrant(a[idx]) && cross(a[last], a[idx]) == 0)ans[a[idx].id] = lastcnt, ++cnt;elseans[a[idx].id] = ++cnt, lastcnt = cnt;}elseans[a[idx].id] = ++cnt, lastcnt = cnt;last = idx;}for(int i = 1; i <= n; i++){cout<<ans[i];if(i != n)cout<<" ";}return 0;}
 能否表示成
能否表示成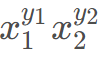 的形式,其中
的形式,其中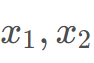 为正整数
为正整数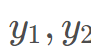 为大于等于2 22的正整数。
为大于等于2 22的正整数。 次询问。
次询问。Tag:数论
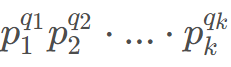 ,首先要满足
,首先要满足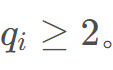
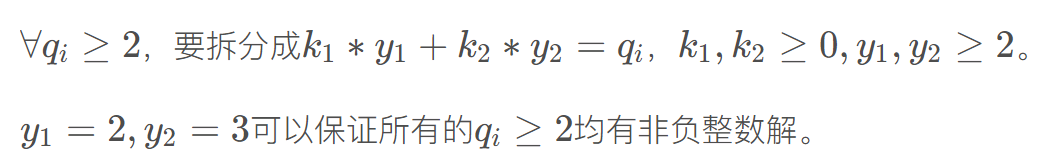

所以问题变成数字a 能否变成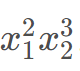 。
。
对于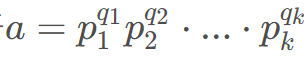 ,只需要检测每个
,只需要检测每个 是否大于等于2即可,只要大于等于2 22就可以按照对应的
是否大于等于2即可,只要大于等于2 22就可以按照对应的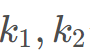 分配到
分配到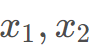 里面。
里面。
由于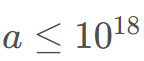 ,所以
,所以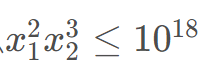 。如果素因子
。如果素因子 。所以只需要暴力判断4000以内的素因子,对于大于4000 的p ,指数只可能是2 , 3 , 4 ,即判断一下是否为平方数或者立方数即可。
。所以只需要暴力判断4000以内的素因子,对于大于4000 的p ,指数只可能是2 , 3 , 4 ,即判断一下是否为平方数或者立方数即可。
时间复杂度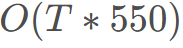 ,550为4000以内素数数量。
,550为4000以内素数数量。
#include<bits/stdc++.h>using namespace std;typedef long long ll;const int MOD = 1e9 + 7;template <typename T>inline T read(T& x) {x = 0;T w = 1;char ch = 0;while (ch < '0' || ch > '9') {if (ch == '-') w = -1;ch = getchar();}while (ch >= '0' && ch <= '9') {x = x * 10 + (ch - '0');ch = getchar();}return x * w;}bool not_prime[4010];int prime[4010], tot;void init(int n){for(int i = 2; i <= n; i++)if(!not_prime[i]){prime[++tot] = i;for(int j = i + i; j <= n; j += i)not_prime[j] = 1;}}inline bool check(ll x){///检查平方数ll y = pow(x, 0.5);if(y * y == x || (y + 1) * (y + 1) == x)return true;///检查立方数y = pow(x, 1.0 / 3);if(y * y * y == x || (y + 1) * (y + 1) * (y + 1) == x || (y + 2) * (y + 2) * (y + 2) == x)return true;return false;}int main(){init(4000);int T;read(T);while(T--){ll x;read(x);if(check(x)){puts("yes");continue;}bool flag = true;for(int i = 1; i <= tot; i++)if(x % prime[i] == 0){int now = 0;while(x % prime[i] == 0){now++;x /= prime[i] ;}///cout<<prime[i]<<" "<<now<<endl;if(now == 1){flag = false;break;}}if(flag & check(x)){puts("yes");continue;}else{puts("no");}}return 0;}
题意:对于数列a ,已知部分区间和,询问若干次区间和。
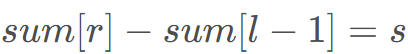 表示,根据差分约束建图准则,相当于点
表示,根据差分约束建图准则,相当于点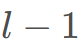 到点 r 长度为s ,r 到
到点 r 长度为s ,r 到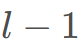 长度为− s。
长度为− s。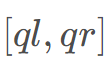 的和,相当于询问
的和,相当于询问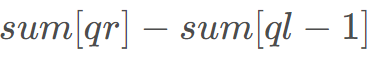 的值。
的值。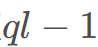 和
和 在同一个连通块中,其次每个连通块只需要随便一个点初始化为0 00,然后按照边长扩展即可。这是由于等号,不管怎么走,相对差值是不变的。
在同一个连通块中,其次每个连通块只需要随便一个点初始化为0 00,然后按照边长扩展即可。这是由于等号,不管怎么走,相对差值是不变的。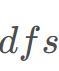 和
和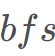 均可以。
均可以。#include<bits/stdc++.h>using namespace std;typedef long long ll;template <typename T>inline T read(T& x) {x = 0;T w = 1;char ch = 0;while (ch < '0' || ch > '9') {if (ch == '-') w = -1;ch = getchar();}while (ch >= '0' && ch <= '9') {x = x * 10 + (ch - '0');ch = getchar();}return x = x * w;}const int maxn = 1e5 + 10;const ll INF = -1e13;int n, m, q;struct edge{int v; ll w;edge(){}edge(int v, ll w):v(v), w(w){}};vector<edge>Map[maxn];ll sum[maxn];bool vis[maxn];void dfs(int u, ll d){vis[u] = 1;sum[u] = d;///cout<<u<<" "<<d<<endl;for(auto x : Map[u]){int v = x.v; ll w = x.w;if(vis[v])continue;dfs(v, d + w);}}queue<pair<int,ll> >Q;void bfs(int u, ll d){vis[u] = 1;sum[u] = d;Q.push(make_pair(u, d));while(!Q.empty()){auto now = Q.front();Q.pop();int u = now.first; ll d = now.second;for(auto x : Map[u]){int v = x.v; ll w = x.w;if(vis[v])continue;vis[v] = 1;sum[v] = d + w;Q.push(make_pair(v, d + w));}}}int f[maxn];int Find(int x){return x == f[x] ? x : f[x] = Find(f[x]);}int main(){read(n);read(m);read(q);for(int i = 0; i <= n; i++)f[i] = i;for(int i = 1; i <= m; i++){int l, r; ll s;read(l);read(r);read(s);///cout<<l<<" "<<r<<" "<<s<<endl;///sum[r] - sum[l - 1] = sMap[l - 1].push_back(edge(r, s));Map[r].push_back(edge(l - 1, -s));f[Find(l - 1)] = Find(r);}for(int i = 0; i <= n; i++)if(!vis[i])bfs(i, 0);while(q--){int l, r;read(l), read(r);--l;if(Find(l) != Find(r))puts("UNKNOWN");else printf("%lld\n", sum[r] - sum[l]);}return 0;}
《算法竞赛》系列推文正在连载中,欢迎持续关注!

扫码优惠购书














