
在我们生活的21世纪,人工智能技术已经达到了相当发达的水平。
但是你知道吗?这门重要的科学早在 2000 多年前就已形成了雏形!
它源于我们人类中的智者对于复杂现象背后的逻辑和推理的研究。
从“如果……那么……”到“弱三段论
从小到大,我们经常会听到“如果……那么……”的句式:
“如果你考试考了一百分,那么爸爸妈妈就带你出去旅游”
“如果你多看书,那么你就能够有更多的知识储备”。
这种在生活中非常普遍的句式中其实蕴含着一种最常见的“逻辑关系”。
那么你有没有想过,这种 “如果……那么……”的句式,是从什么时候开始流传的?
事实上,这种简单的逻辑关系,可以追溯到公元前5世纪的古希腊!
如果你学过编程,你可能会说,这就是计算机语言中的“if…then…”呀!
是的,只不过当时这种语法不是用来编程的,而常常被用来做否定的推理。
我们来看图 1 中的例子。
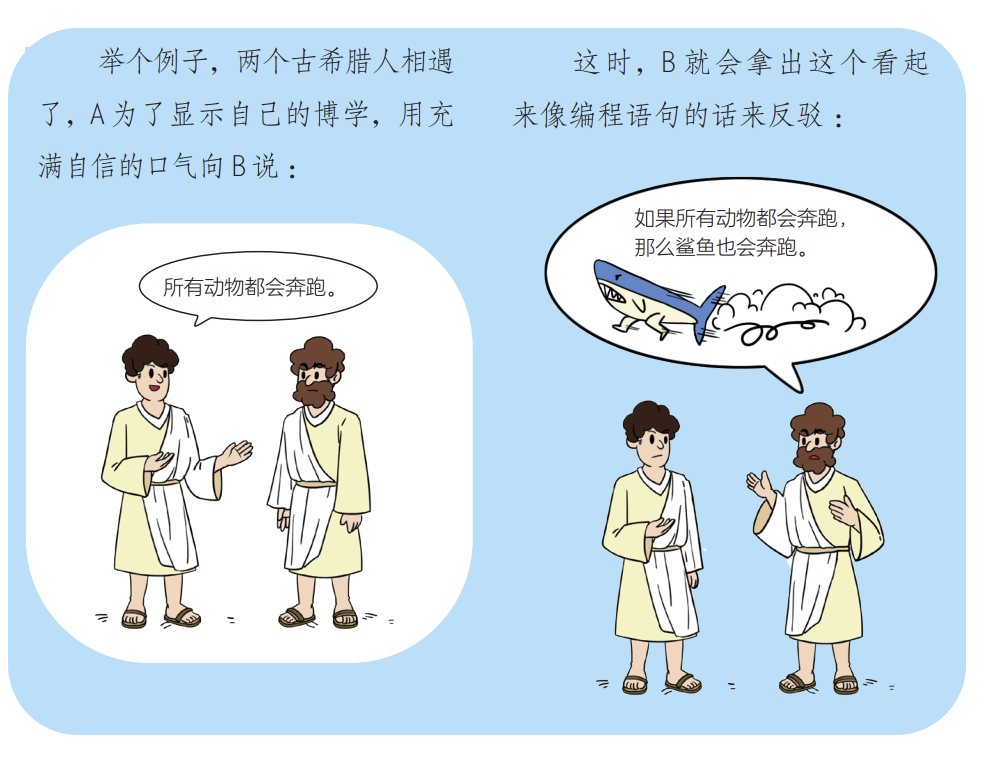
■ 图1 基于常识的逻辑推理
根据常识,我们很容易知道A 说的话是错的,这便是最简单的逻辑推理。
但是这种推理需要推理者具有一定的经验常识。假设A不知道鲨鱼是什么,那么B可能就无法说服他。
不要觉得这样的对话很奇怪!古希腊社会非常崇尚演讲和辩论,这样的交谈方式并不罕见。在这些辩论的过程中,人们也在不断思考如何进行辩论,这就促进了逻辑学的发展。
柏拉图曾提出过一种名为“划分法”的辩论方法。他说 :
“所有动物要么是会死的,要么是不朽的,
人是动物,
所以人要么是会死的,要么是不朽的。”
在这段话中,第一行似乎是一个大前提,第二行成为一个小前提,第三行得出了结论。
看上去,划分法已经形成了三段论的雏形。亚里士多德的《前分析篇》中认为,划分法是一种“弱三段论”。
但划分法与真正的三段论还是有些区别的——这种“弱三段论”的结论并不是一个确定的推论,而是两种可能性。
亚里士多德和他的三段论
亚里士多德在他的著作《前分析篇》中提出了三段论的逻辑分析方法,并给出了三段论 的定义:“只要确定某些论断,某些异于它们的事物便必然可以从这些确定的论断中推出。”
这句话单拿出来看有点抽象,把它解释成一句通俗易懂的话就是:
“只要给出了确定的大前提和小前提,就能推出确切的结论。”
亚里士多德曾经就“苏格拉底之死”这件事提出了一段著名的三段论,如图2所示。
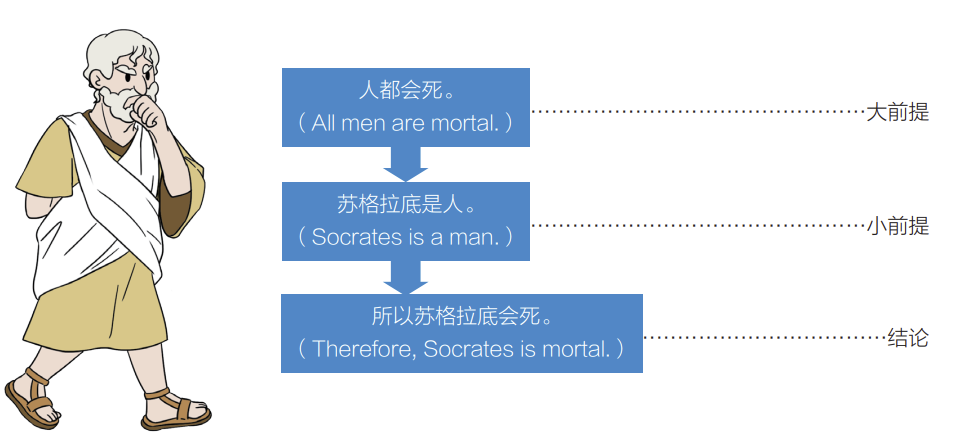
■ 图2 亚里士多德的三段论
美国导演伍迪·艾伦(Woody Allen)以此衍生了他戏谑式的“三段论”,如图3所示。

■ 图3 伍迪·艾伦的“三段论”
伍迪·艾伦所谓的“三段论”当然是荒谬的。这也说明了虽然三段论看起来比较简单,但要保证准确,其实它的内在还存在很多复杂的规则。
譬如,在《前篇分析》中,亚里士多德为三段论设置了一些基本规则:
1. 必须有一个前提是肯定的,并且必须有一个前提是全称命题;
2. 两个前提中否命题的数目必须与结论中否命题的数目相同;
3. 每个证明都是且只能是通过三个词项得到的。
为了方便记忆,我们把 3 条规则分别叫作“全称命题”“数目相同”“三个词项”。
仅看规则不免有些晦涩,我们不妨通过“苏格拉底之死”的例子来理解三段论的规则。
(1)在“苏格拉底之死”的三段论中,两个前提分别是“人都会死”和“苏格拉底是人”,两个命题都是肯定的,且“人都会死”是一个全称命题,符合第 1 条“全称命题”的规则。
(2)结论是肯定的,两个前提也是肯定的,满足第 2 条“数目相同”的条件。
(3)这个证明是通过“人”“苏格拉底”和“死”这 3 个词来证明的,符合第 3 个“三个词项”的规则。
好了,我们现在可以举一些看起来很离谱的反例,来验证这些规则的正确性。
对于第 1 条规则,如果三段论中没有全称命题,则可能出现图 4 中展现的情况。

■ 图4 违反第1条规则的三段论
对于第2条规则,如果前提和结论中否命题数目不同,则可能出现图5中展现的情况。

■ 图5 违反第2条规则的三段论
对于第 3 条规则,如果一段证明中出现了 4 个词项,可能会得出下列论断:“所有人都会死,苏格拉底是人,所以凯撒会死。”
无辜的凯撒was like:

所以说,对于一个有效的三段论,亚里士多德提出的3条规则是缺一不可的。
引入变项
亚里士多德在《后分析篇》中采用变项来表示某一特征或某一内容,类似于计算机中的“赋值”。
他用 A 来表示肯定的命题,用 E 表示否定,认为所有的三段论都可以转化为 AAA 或 EAE 两种形式,如图6所示。
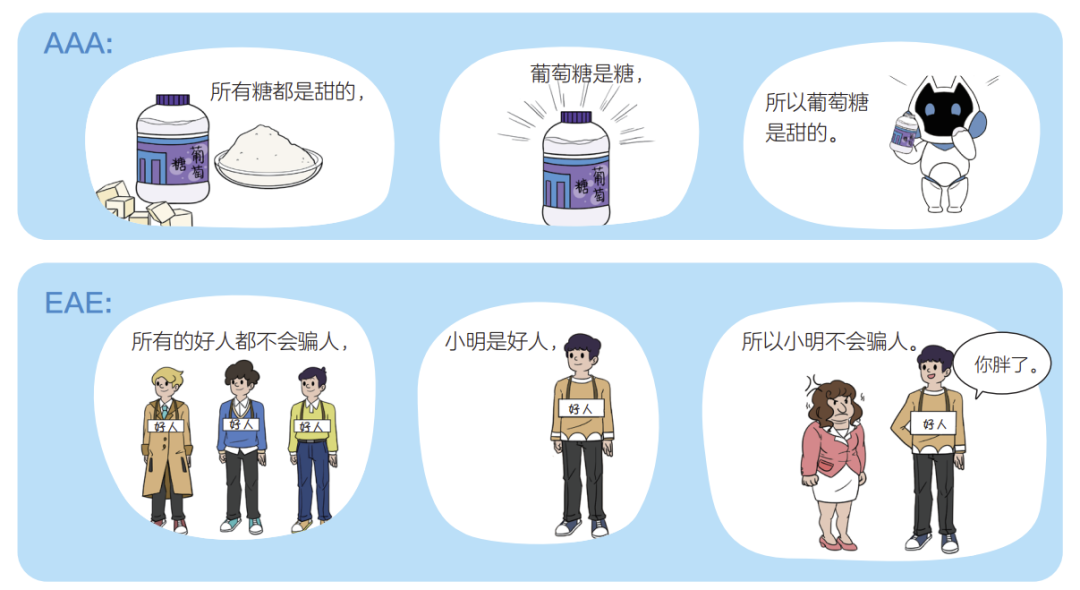
■ 图6 三段论的两种形式
(亚里士多德还将他的三段论划分为 3 个格式和 14 个有效形式,具体内容我们就不在这里细述了。)
这套推理系统中已经出现了现代逻辑公理系统的雏形,保证了逻辑推理系统的有效性和必然性,也保证了推理结果是“逻辑真理”。
得到“逻辑真理”这点在逻辑分析中至关重要。在这套逻辑推理系统产生前,若想对某 些事物进行判断,依靠的是个人经验。然而我们知道,人们的经验终究是有限的,因此能够做出判断的内容也是有限的。
而根据亚里士多德的逻辑推理系统,人们可以不依赖经验事实,而只通过逻辑分析的方法得到“逻辑真理”。
亚里士多德的逻辑推理系统对于逻辑学的发展有重大意义,同样对计算机的发展也具有重要意义——
我们都知道,计算机就是一个典型的并不存在生活经验的物件。因此人们需要给它制定一套完全不依赖经验的“逻辑真理”的体系,才能让它在运行时做出正确的推断。
乌鸦悖论
亚里士多德的三段论推理系统保证了推理所得的结果是“逻辑真理”。
而逻辑学的有趣之处在于,一些在逻辑学中被认为正确的事情可能会与人们的直觉相矛盾,让人们很难理解和接受。
比如我们现在抛出一个小问题!↓↓↓↓↓↓↓↓↓↓↓↓
“树叶是绿色的”和“乌鸦是黑色的”之间存在什么关系吗?

你可能会被这个突然出现的问题困惑住:这能有什么关系呢?别着急,我们下面细说一下二者之间的关系。
先来看一个命题 :“所有乌鸦都是黑色的”。
我们已经看过了几百只乌鸦,它们都是黑色的(事实上,“乌鸦”的“乌”不就说明它是黑色的吗?😊),我们就使用归纳法,认为乌鸦都是黑色的,也就相信这一命题是真的。
之后我们每看到一只黑色的乌鸦都会让我们更加确信,这一命题为真。
我们都知道,在数学上有一个“逆否命题”的概念 :命题“若 A,则 B”的逆否命题是“若非 B,则非 A”。而一个命题和它的逆否命题在逻辑上是等价的。
如果我们认为原命题“所有的乌鸦都是黑色的”为真,那么它的逆否命题即“所有不是黑色的东西都不是乌鸦”也是真命题。
所以说,每当我们看到一棵绿色的大树、一盏蓝色的台灯、一只褐色的烤鸭时,我们就让“所有乌鸦都是黑色的”这一命题的可信度又增加了一分。
这在概率论学科中称为贝叶斯概率。
在我们的直觉中,看到一棵绿树、一张白纸,这些与乌鸦似乎并没有任何关系,但却要接受我们已经“在逻辑上增加了乌鸦颜色命题的可信度”的事实,这往往令我们很难理解。
这就是著名的乌鸦悖论,它是一个人们的直觉和感性的认知与逻辑学中的理性判断之间存在矛盾的著名案例。
我们再来看另外一个例子。
图7展示了 4 张卡片,每张卡片一面是字母,另一面是数字。

■ 图7 四张卡片
我们现在想要验证下面这一条命题是否正确 :
“如果卡片一面印有元音(A、E、I、 O、U),那么另一面会是偶数”
那么我们应该选择翻看哪两张卡片来验证呢?
很多人第一直觉想到的是翻看 A 和 4,看元音 A 后面是不是偶数,看偶数 4 后面是不是元音。但是仔细思考一下,你会发现实际要验证的命题是:
如果一面是元音,那么另一面是偶数。
没有说偶数的另外一面是元音。
所以无论 4 后面是不是元音,都无法支持或反对上面的规则。
而跟上面命题等价的逆否命题是 :如果一面不是偶数,那么另一面不是元音。
于是,实际上我们需要翻的两张卡片是 A,以及卡片里唯一的奇数 7。
翻看卡片 A 背面是否为偶数可以直接验证命题,翻看卡片 7 背面是否为“非元音字母” 则可以验证其逆否命题,也是在间接验证命题本身。
所以……乌鸦悖论,你学会了吗?

精彩预告
三段论是什么,它与人工智能有哪些关系?
计算机是怎样从笨重的庞然大物变成如今千家万户的必需品的?
如何理解看起来高深莫测的计算机算法?
如何判断和你在网上对话的“人”是不是一台电脑?
所谓的“机器学习”如何理解,机器是如何学习的?
机器视觉是怎么一回事?机器如何感知万物?
我们未来应该如何与人工智能共存?
想要了解更多AI相关的科普内容,欢迎购买清华大学出版社新书《漫话人工智能:从二进制到未来智能社会》!
参考书籍


扫码优惠购书
《漫话人工智能:从二进制到未来智能社会》是一本非常适合大众读者尤其是青少年读者阅读的人工智能通识读物,将生动风趣的语言与精美的手绘插画结合,采用全彩印刷,兼具内容的专业性与形式上的趣味性。作者秦曾昌博士在书中不仅深入浅出、图文并茂地勾勒了人工智能的前世今生,并且放眼未来,提供了认识人工智能未来走向的视角。本书获姬十三、郑永春等科普大V联袂推荐,并入选中国科协2022年“科普中国出版创作扶持计划”。















