我们在上一篇文章中介绍了5种最基础的、基于规则策略的排序算法,那些算法是在没有足够的用户行为数据的情况下不得已才采用的方法,一旦我们有了足够多的行为数据,那么我们就可以采用更加客观、科学的机器学习排序算法了。
12.1 logistics回归排序算法
12.1.1 logistics回归的算法原理
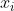 是特征,
是特征,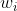 是模型的参数)是简单的线性模型,原理简单,易于理解,并且非常容易训练,对于一般的分类及预测问题,可以提供简单的解决方案。
是模型的参数)是简单的线性模型,原理简单,易于理解,并且非常容易训练,对于一般的分类及预测问题,可以提供简单的解决方案。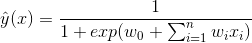
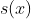 就是logistics变换,对比公式1和公式2,大家应该可以看到logistics回归模型就是将线性模型通过logistics变换获得的。
就是logistics变换,对比公式1和公式2,大家应该可以看到logistics回归模型就是将线性模型通过logistics变换获得的。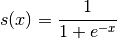
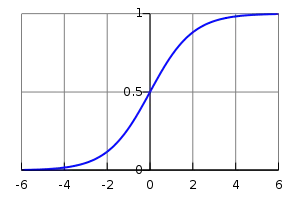
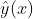 (公式1的左边)变换到0到1之间,因此logistics回归可以看成是预测变量的概率估计,所以对于预测点击率(或二分类问题)这类业务是非常直观实用的。
(公式1的左边)变换到0到1之间,因此logistics回归可以看成是预测变量的概率估计,所以对于预测点击率(或二分类问题)这类业务是非常直观实用的。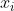 就是各类特征(用户维度特征、物品维度特征、用户行为特征、上下文特征等),而预测值
就是各类特征(用户维度特征、物品维度特征、用户行为特征、上下文特征等),而预测值 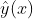 就是该用户对物品的点击概率。那么最终的推荐排序就是先计算该用户对每个物品(这些物品是召回阶段的物品)的点击概率,然后基于点击概率降序排列,再取topN作为最终的推荐结果。下面图2就可以很好地说明logistics回归模型怎么用于推荐系统相关的预测中。
就是该用户对物品的点击概率。那么最终的推荐排序就是先计算该用户对每个物品(这些物品是召回阶段的物品)的点击概率,然后基于点击概率降序排列,再取topN作为最终的推荐结果。下面图2就可以很好地说明logistics回归模型怎么用于推荐系统相关的预测中。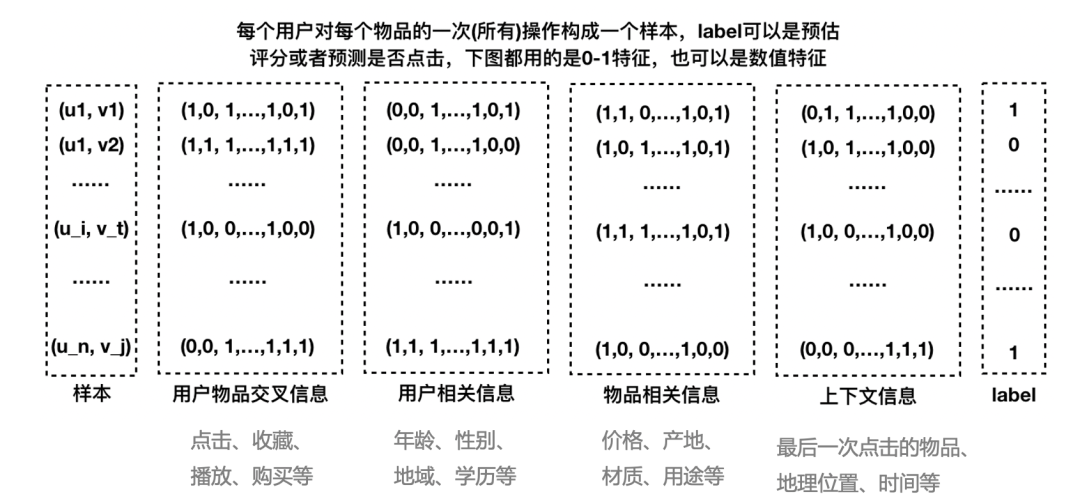
12.1.2 logistics回归的特点
12.1.3 logistics回归的工程实现
12.1.4 logistics回归在业界的应用
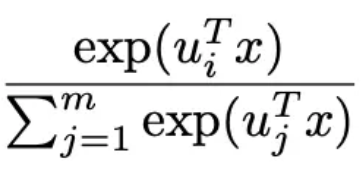 部分),见下面的公式3。当m=1时就是普通的logistics回归模型,当m大时,预估的会越准,但是这时参数也越多,需要更多的训练样本、更长的训练时间才能训练出有效果保证的模型。
部分),见下面的公式3。当m=1时就是普通的logistics回归模型,当m大时,预估的会越准,但是这时参数也越多,需要更多的训练样本、更长的训练时间才能训练出有效果保证的模型。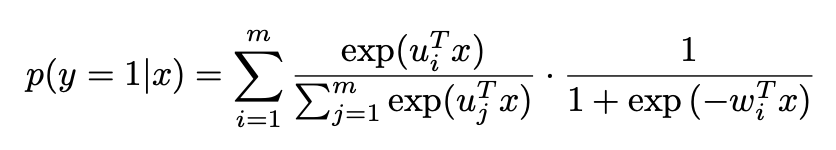
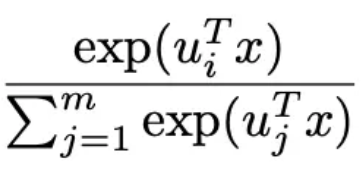 类似于注意力机制的注意力参数。关于这个模型的细节介绍,大家可以阅读参考文献3,这里不展开说明了。
类似于注意力机制的注意力参数。关于这个模型的细节介绍,大家可以阅读参考文献3,这里不展开说明了。12.2 FM排序算法
12.2.1 FM的算法原理
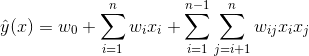
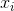 是第i个特征的值,
是第i个特征的值,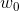 、
、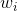 、
、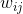 是模型参数,只有当
是模型参数,只有当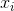 与
与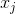 都不为0时,交叉项才有意义。
都不为0时,交叉项才有意义。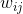 训练不充分而不准确,最终影响模型的效果。特别是对于推荐、广告等这类数据非常稀疏的业务场景来说(这些场景的最大特点就是特征非常稀疏,推荐是由于标的物是海量的,每个用户只对很少的标的物有操作,因此很稀疏,广告是由于很少有用户去点击广告,点击率很低,导致收集的数据量很少,因此也很稀疏),很多特征之间交叉是没有(或者没有足够多)训练数据支撑的,因此无法很好地学习出对应的模型参数。因此上述整合二阶两两交叉特征的模型并未在工业界得到广泛采用。
训练不充分而不准确,最终影响模型的效果。特别是对于推荐、广告等这类数据非常稀疏的业务场景来说(这些场景的最大特点就是特征非常稀疏,推荐是由于标的物是海量的,每个用户只对很少的标的物有操作,因此很稀疏,广告是由于很少有用户去点击广告,点击率很低,导致收集的数据量很少,因此也很稀疏),很多特征之间交叉是没有(或者没有足够多)训练数据支撑的,因此无法很好地学习出对应的模型参数。因此上述整合二阶两两交叉特征的模型并未在工业界得到广泛采用。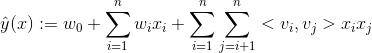
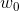 、
、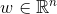 、
、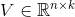 。
。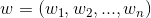 ,是n维向量。
,是n维向量。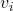 、
、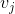 是低维向量(k维),类似矩阵分解中的用户或者标的物特征向量表示。V是由
是低维向量(k维),类似矩阵分解中的用户或者标的物特征向量表示。V是由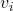 组成的矩阵。< , > 是两个k维向量的内积:
组成的矩阵。< , > 是两个k维向量的内积: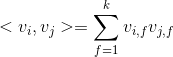
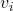 就是我们的FM模型核心的分解向量,k是超参数,一般取值较小(100左右)。
就是我们的FM模型核心的分解向量,k是超参数,一般取值较小(100左右)。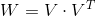 (Cholesky decomposition)。这说明,FM这种通过分解的方式基本可以拟合任意的二阶交叉特征,只要分解的维度k足够大(首先,
(Cholesky decomposition)。这说明,FM这种通过分解的方式基本可以拟合任意的二阶交叉特征,只要分解的维度k足够大(首先,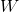 的每个元素都是两个向量的内积,所以一定是对称的,另外,分解机的公式中不包含
的每个元素都是两个向量的内积,所以一定是对称的,另外,分解机的公式中不包含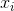 与
与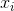 自身的交叉,这对应矩阵
自身的交叉,这对应矩阵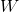 的对角元素,所以我们可以任意选择
的对角元素,所以我们可以任意选择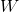 对角元素足够大,保证
对角元素足够大,保证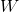 是半正定的)。由于在稀疏情况下,没有足够的训练数据来支撑模型训练,一般选择较小的k,虽然模型表达空间变小了,但是在稀疏情况下可以达到较好的效果,并且有很好的拓展性。
是半正定的)。由于在稀疏情况下,没有足够的训练数据来支撑模型训练,一般选择较小的k,虽然模型表达空间变小了,但是在稀疏情况下可以达到较好的效果,并且有很好的拓展性。12.2.2 FM的参数估计
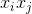 与
与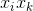 ,它们的系数
,它们的系数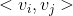 和
和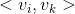 共用一个相同的向量
共用一个相同的向量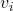 )。
)。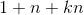 ,而整合两两二阶交叉的线性模型的系数个数为
,而整合两两二阶交叉的线性模型的系数个数为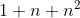 。分解机的系数个数是n的线性函数,而整合交叉项的线性模型系数个数是n的指数函数,当n非常大时,训练分解机模型在存储空间及迭代速度上是非常有优势的。
。分解机的系数个数是n的线性函数,而整合交叉项的线性模型系数个数是n的指数函数,当n非常大时,训练分解机模型在存储空间及迭代速度上是非常有优势的。12.2.3 FM的计算复杂度
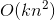 。但是我们可以通过适当的公式变换与数学计算,将模型复杂度降低到
。但是我们可以通过适当的公式变换与数学计算,将模型复杂度降低到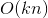 ,变成线性复杂度的预测模型,具体推导过程如下:
,变成线性复杂度的预测模型,具体推导过程如下: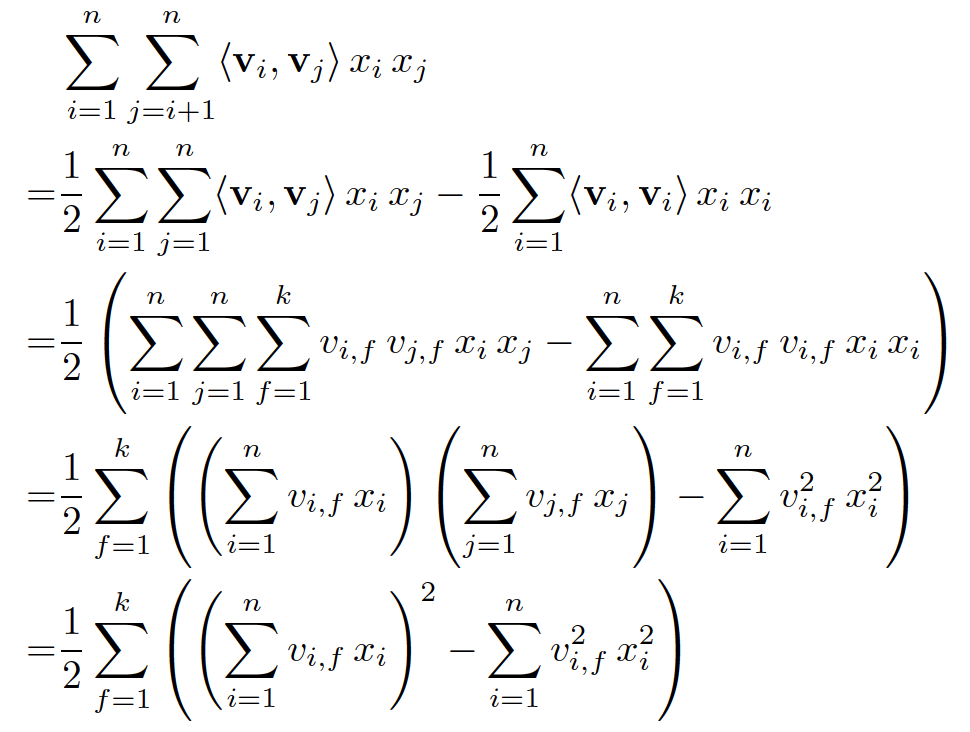
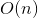 ,加上外层的
,加上外层的 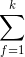 ,最终的时间复杂度是
,最终的时间复杂度是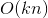 。进一步地,在数据稀疏情况下,大多数特征x为0,我们只需要对非零的x求和,因此,时间复杂度其实是
。进一步地,在数据稀疏情况下,大多数特征x为0,我们只需要对非零的x求和,因此,时间复杂度其实是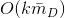 ,
,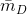 是训练样本中平均非零的特征个数。
是训练样本中平均非零的特征个数。12.2.4 FM求解
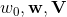 )可以在工程实现上高效地利用梯度下降算法(SGD、ALS等)来训练(即我们可以线性时间复杂度求出下面的
)可以在工程实现上高效地利用梯度下降算法(SGD、ALS等)来训练(即我们可以线性时间复杂度求出下面的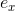 ,所以在迭代更新参数时是非常高效的,见下面的迭代更新参数的公式)。结合公式5和公式6,我们很容易计算出FM模型的梯度如下:
,所以在迭代更新参数时是非常高效的,见下面的迭代更新参数的公式)。结合公式5和公式6,我们很容易计算出FM模型的梯度如下: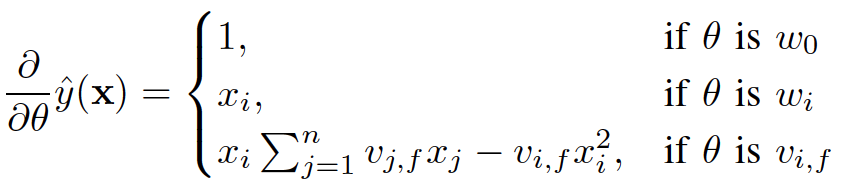
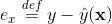 ,针对平方损失函数,具体的参数更新公式如下(未增加正则项,其他损失函数的迭代更新公式类似,也可以很容易推导出):
,针对平方损失函数,具体的参数更新公式如下(未增加正则项,其他损失函数的迭代更新公式类似,也可以很容易推导出):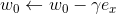
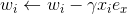
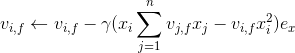
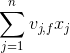 与i无关,因此可以事先计算出来(在做预测求
与i无关,因此可以事先计算出来(在做预测求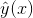 或者在更新参数时,这两步都需要计算该量)。上面的梯度计算可以在常数时间复杂度
或者在更新参数时,这两步都需要计算该量)。上面的梯度计算可以在常数时间复杂度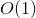 下计算出来。在模型训练更新时,在
下计算出来。在模型训练更新时,在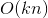 时间复杂度下完成对样本
时间复杂度下完成对样本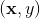 的更新(如果是稀疏情况下,更新时间复杂度是
的更新(如果是稀疏情况下,更新时间复杂度是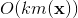 ,
, 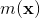 是特征
是特征 非零元素个数)。
非零元素个数)。12.2.5 FM进行排序的方法
回归问题(Regression)
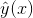 直接作为预测项,可以转化为求最小值的最优化问题,具体如下:
直接作为预测项,可以转化为求最小值的最优化问题,具体如下: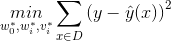
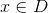 对应的真实值。
对应的真实值。二元分类问题 (Binary Classification)
12.3 GBDT排序算法
12.3.1 GBDT的算法原理
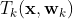 是第i棵决策树,其中
是第i棵决策树,其中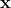 是模型的特征,
是模型的特征,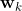 是树的参数,
是树的参数,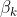 是各棵树的权重。
是各棵树的权重。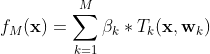

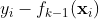 是当前模型
是当前模型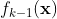 在样本点
在样本点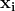 第k步的残差,我们学习一个新的树
第k步的残差,我们学习一个新的树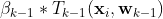 来拟合残差
来拟合残差 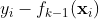 。所有样本点上的残差之和就是整个训练样本在第k次迭代的残差(见下面公式)。
。所有样本点上的残差之和就是整个训练样本在第k次迭代的残差(见下面公式)。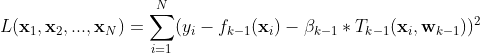
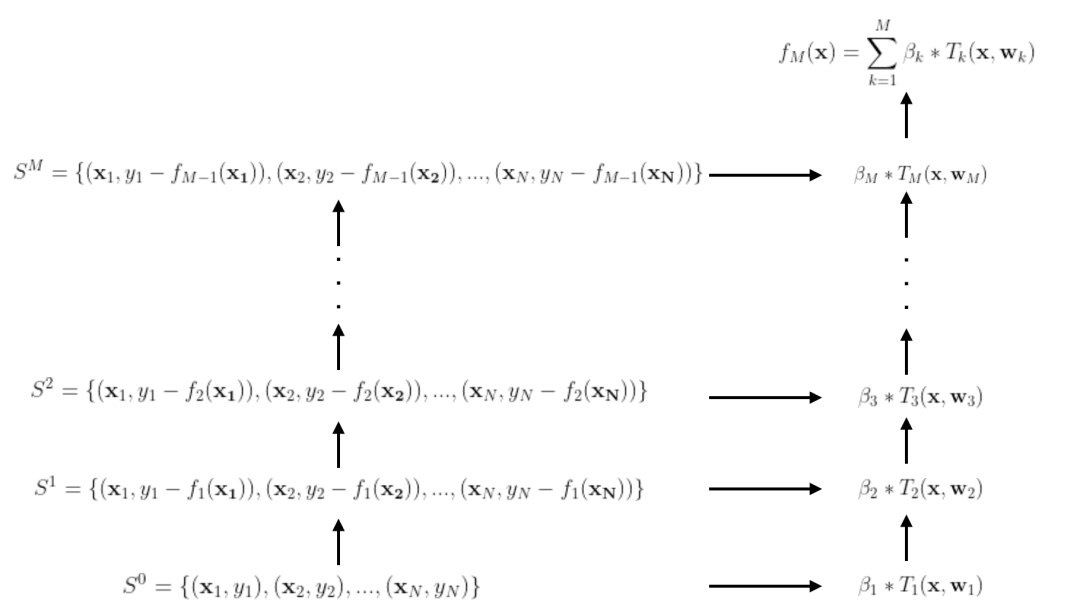
12.3.2 GBDT用于推荐排序
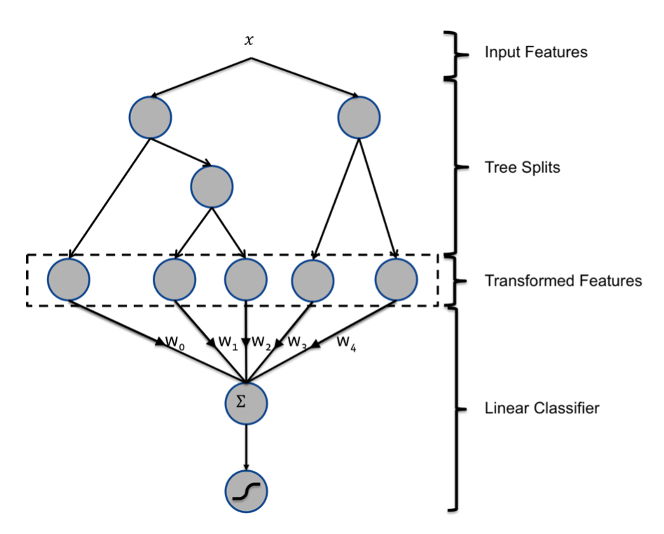
总结
参考文献
https://spark.apache.org/docs/latest/ml-classification-regression.html#logistic-regression Ad Click Prediction- a View from the Trenches 【2017 阿里】Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction 【2010】 Factorization Machines https://github.com/srendle/libfm https://spark.apache.org/docs/latest/ml-classification-regression.html#factorization-machines-classifier https://spark.apache.org/docs/latest/ml-classification-regression.html#factorization-machines-regressor https://en.wikipedia.org/wiki/Gradient_boosting https://web.njit.edu/~usman/courses/cs675_fall16/BoostedTree.pdf [2001] Greedy function approximation: a gradient boosting machine http://www.chengli.io/tutorials/gradient_boosting.pdf https://github.com/dmlc/xgboost https://github.com/microsoft/LightGBM https://spark.apache.org/docs/latest/ml-classification-regression.html#gradient-boosted-tree-classifier https://spark.apache.org/docs/latest/mllib-ensembles.html#gradient-boosted-trees-gbts https://xgboost.readthedocs.io/en/latest/jvm/xgboost4j_spark_tutorial.html https://github.com/microsoft/SynapseML 【2014 GBDT+LR】Practical Lessons from Predicting Clicks on Ads at Facebook
大家如果想更全面学习推荐系统,可以购买作者之前出版的图书,购买链接如下:

文章转载自数据与智能,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






