.3.导读编者按
该论文由北京大学王选计算机研究所邹磊课题组完成,是SIGMOD 2021 论文《Sliding Window-based Approximate Triangle Counting over Streaming Graphs with Duplicate Edges》的扩展版本。由于很多图模型应用场景对于动态性的天然需求,图流分析近年来得到了越来越多的关注。由于图流规模大,更新速度快的特点,对其进行精确存储和分析从时间和空间上都有巨大的代价。相比之下高效的近似查询算法是一种更好的选择。此外,由于很多应用对于时效性的需求,降低图流中旧数据项的重要性,并在适当时机删除它们往往也是必需的。这种老化机制一般被描述为滑动窗口模型。然而,在滑动窗口模型下,对含重复边的图流进行近似三角形计数依然是一个有待解决的问题。本文中,我们提出了名为SWTC (Sliding Window Triangle Counting) 的算法。该算法使用独创策略来维护一个基于滑动窗口的无偏的,限定大小的样本,从而实现对滑动窗口内三角形数目的估算。实验表明该算法相比已有工作组合而成的基准算法,具有更高的准确度。

1 背景介绍
三角形计数是图上的基本问题之一。大量的应用,如社区发现 [1],异常探测 [2] 等都是以三角形计数为基础的。大规模图数据上的精确三角形计数需要消耗大量时间,因此往往采用近似算法作为替代,相关方法在最近的十几年内已经得到了广泛的研究。然而,随着互联网的不断发展,图数据的组织形式有了新的变化。在社交网络,通信网络等应用中产生的图数据往往被组织为图流的形式,即一系列持续不断到达的边。在这条边序列中,相同的边可能出现多次,即重复边 (duplicate edge)。此外,由于图流数据会持续不断地产生,对全部的图流数据进行存储和分析是十分困难的。而且大多数应用都对数据具有时效性的要求。因此,我们在处理图流时往往采用滑动窗口 (sliding window) 模型,即只分析最近的一段时间内到达的边组成的动态图。在滑动窗口模型下对含重复边的图流数据进行近似三角形计数仍是一个有待研究的领域。我们的论文对这一问题进行了研究,提出了滑动窗口三角形近似计数算法 SWTC (sliding window triangle counting)。
2 问题定义
图流 (streaming graph):如上文所说,图流为一个持续不断到达的边组成的序列,序列的每一个元素为两个点之间的一条边。这条边可以有向也可以无向。在三角形计数问题中,三角形的定义一般是无向的,因此我们在此问题中将图流中的边也考虑为无向。每一个元素还具有一个时间戳,标识元素到达的时间。同一条边在图流中可以出现多次,即为重复边 (duplicate edge)。
3 SWTC算法
SWTC 算法为基于采样的近似计数算法,即维护一个从快照图中抽取出的小规模样本图,在此样本图中计数三角形数目,以此来估算整个快照图中的三角形数目。根据二项计数还是带权计数的选择不同,采样和估算的方法也会有所区别,我们首先以二项计数为例说明算法,之后再推广到带权计数上。在用SWTC 对三角形数目进行二项计数时,算法可以大概分为两部分,样本图的维护,以及估算滑动窗口内的互异边数目,最终我们将根据两部分的结果估算快照图中的三角形数目。下面我们对两部分分别进行介绍:
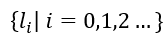 , 并用
, 并用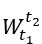 表示从时刻
表示从时刻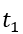 到
到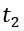 图流中到达的边,
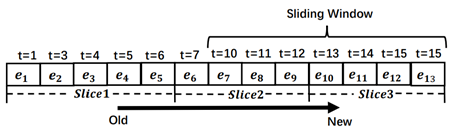
图流中到达的边,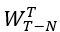 表示滑动窗口。图1中也展示了片段的示例,滑动窗口和片段均为6个时间单元。显然,滑动窗口最多与两个片段相交,我们将这两个片段记为
表示滑动窗口。图1中也展示了片段的示例,滑动窗口和片段均为6个时间单元。显然,滑动窗口最多与两个片段相交,我们将这两个片段记为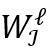 与
与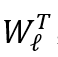 , 其中
, 其中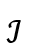 与
与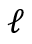 为 T 之前最近的两个路标。当前时刻 T 正好在一个路标上时,滑动窗口只和最近的一个片段相交。我们在每个子流
为 T 之前最近的两个路标。当前时刻 T 正好在一个路标上时,滑动窗口只和最近的一个片段相交。我们在每个子流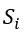 中,维护最近两个片段里优先级最大的边,记为 β[i] 与 ϵ[i]。这一过程较为简单,因为每个片段的起始和结束时刻都是确定的,对于片段
中,维护最近两个片段里优先级最大的边,记为 β[i] 与 ϵ[i]。这一过程较为简单,因为每个片段的起始和结束时刻都是确定的,对于片段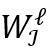 , 我们只需要在
, 我们只需要在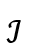 时刻开始维护一个变量β[i],并在每次有新的边被划分到子流
时刻开始维护一个变量β[i],并在每次有新的边被划分到子流 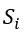 中时,比较其优先级与 β[i]的优先级,若新边具有更高优先级,则替换 β[i],直到时刻
中时,比较其优先级与 β[i]的优先级,若新边具有更高优先级,则替换 β[i],直到时刻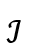 。同理我们也可以只用一个变量来维护
。同理我们也可以只用一个变量来维护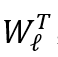 内优先级最高的边ϵ[i]。之后我们根据二者的时间戳和优先级,选择其中至多一个作为此子流中的样本。
内优先级最高的边ϵ[i]。之后我们根据二者的时间戳和优先级,选择其中至多一个作为此子流中的样本。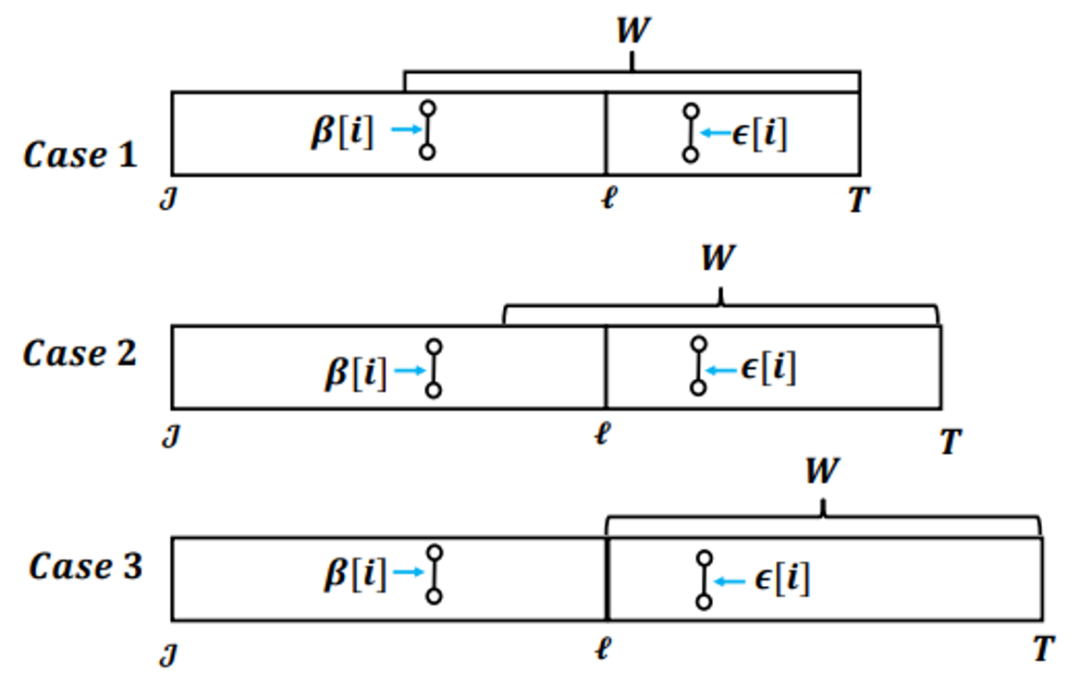
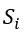 中存在三种情况。第一种情况是β[i] 与ϵ[i]均在滑动窗口内,我们将其中优先级更高的记录为
中存在三种情况。第一种情况是β[i] 与ϵ[i]均在滑动窗口内,我们将其中优先级更高的记录为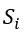 中的样本。第二种情况则是 ϵ[i]已经过期,然后滑动窗口仍与片段
中的样本。第二种情况则是 ϵ[i]已经过期,然后滑动窗口仍与片段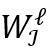 相交。此时我们比较β[i]与 ϵ[i]的优先级,若
相交。此时我们比较β[i]与 ϵ[i]的优先级,若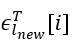 的优先级更高(或相同),则我们可以选择其为该子流中的样本,因为
的优先级更高(或相同),则我们可以选择其为该子流中的样本,因为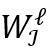 中的所有边优先级都不超过β[i],自然也不超过ϵ[i],而 ϵ[i]自身又是
中的所有边优先级都不超过β[i],自然也不超过ϵ[i],而 ϵ[i]自身又是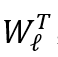 内优先级最高的边,因此其为整个
内优先级最高的边,因此其为整个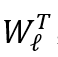 内优先级最高的边,自然也是滑动窗口内优先级最高的边。而如果ϵ[i]的优先级小于β[i],那么我们无法将其选为样本边,因为在
内优先级最高的边,自然也是滑动窗口内优先级最高的边。而如果ϵ[i]的优先级小于β[i],那么我们无法将其选为样本边,因为在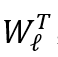 与滑动窗口的相交区域内,可能存在边优先级高于ϵ[i] 而小于β[i]。此种情况下我们无法在此子流选出样本边。随着时间推移,情况二会演变为情况三,即为滑动窗口只与
与滑动窗口的相交区域内,可能存在边优先级高于ϵ[i] 而小于β[i]。此种情况下我们无法在此子流选出样本边。随着时间推移,情况二会演变为情况三,即为滑动窗口只与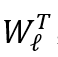 相交,此时我们可以选择 β[i] 为样本边。之后情况三会再演变为情况一,三种情况交替出现。
相交,此时我们可以选择 β[i] 为样本边。之后情况三会再演变为情况一,三种情况交替出现。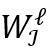 与
与 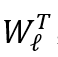 中优先级最高的边在滑动窗口内时,我们才可以在该子流中选出样本。因此,每个子流中选出样本边的概率p 为
中优先级最高的边在滑动窗口内时,我们才可以在该子流中选出样本。因此,每个子流中选出样本边的概率p 为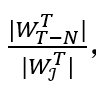 , 其中 | ∙ | 表示集合内互异元素的数目。这一概率随着时间推移不断变化,当图流流量稳定 (即片段内互异边数目和时间长度成正比时),这一概率在 0.5 到 1 的范围内波动,平均值为 0.75。在此算法中,我们在每一个子流中保存两条边,小消耗的空间大小为 O(k)。
, 其中 | ∙ | 表示集合内互异元素的数目。这一概率随着时间推移不断变化,当图流流量稳定 (即片段内互异边数目和时间长度成正比时),这一概率在 0.5 到 1 的范围内波动,平均值为 0.75。在此算法中,我们在每一个子流中保存两条边,小消耗的空间大小为 O(k)。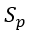 中,比较ϵ[p]的优先级和 e 的优先级,若ϵ[p]的优先级较高,则直接丢弃 e 并结束更新。否则,我们替换ϵ[p]=e,并比较 e 和β[p]的优先级大小,若仍是 e 优先级较高,则将 e 加入样本图,并将该子流中的原样本边从样本图中删除。
中,比较ϵ[p]的优先级和 e 的优先级,若ϵ[p]的优先级较高,则直接丢弃 e 并结束更新。否则,我们替换ϵ[p]=e,并比较 e 和β[p]的优先级大小,若仍是 e 优先级较高,则将 e 加入样本图,并将该子流中的原样本边从样本图中删除。除了维护样本图之外,我们还需要对滑动窗口内互异边数目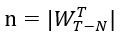 进行估算,这一参数在估算快照图中三角形数目时至关重要。重复边的存在,以及边过期,特别是非样本边的过期(我们无法发觉非样本边的过期,因为我们没有保存它们),使得这一估算十分困难,我们无法直接用已有工作例如 Hyperloglog 算法 [4] 去估算,因为这些算法不支持滑动窗口模型。我们注意到,SWTC已经将图流划分为了若干固定的片段,而Hyperloglog 算法能够在这些片段上实施。因此,我们首先使用Hyperloglog算法估算与滑动窗口相交的两个片段内的互异边的数目,然后再以此为依据估算滑动窗口内的互异边的数目。
进行估算,这一参数在估算快照图中三角形数目时至关重要。重复边的存在,以及边过期,特别是非样本边的过期(我们无法发觉非样本边的过期,因为我们没有保存它们),使得这一估算十分困难,我们无法直接用已有工作例如 Hyperloglog 算法 [4] 去估算,因为这些算法不支持滑动窗口模型。我们注意到,SWTC已经将图流划分为了若干固定的片段,而Hyperloglog 算法能够在这些片段上实施。因此,我们首先使用Hyperloglog算法估算与滑动窗口相交的两个片段内的互异边的数目,然后再以此为依据估算滑动窗口内的互异边的数目。
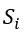 ,我们已经保存了最近的两个片段
,我们已经保存了最近的两个片段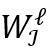 与
与 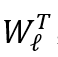 中优先级最高的边,我们取二者中最高的优先级,记为θi。θi是
中优先级最高的边,我们取二者中最高的优先级,记为θi。θi是 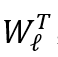 内的所有边优先级的最大值,而这些优先级是由 [0,1) 范围内的均匀分布哈希函数 G(∙) 产生的。我们可以将其转换为一组服从
内的所有边优先级的最大值,而这些优先级是由 [0,1) 范围内的均匀分布哈希函数 G(∙) 产生的。我们可以将其转换为一组服从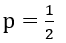 的几何分布的变量
的几何分布的变量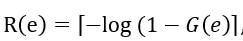 , 则θi为
, 则θi为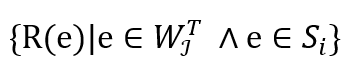 中的最大值,k 个子流中的θi便组成了一个
中的最大值,k 个子流中的θi便组成了一个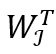 上的 Hyperloglog sketch,我们可以利用其估算|
上的 Hyperloglog sketch,我们可以利用其估算|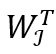 |的值,计算方法为
|的值,计算方法为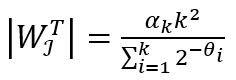 ,其中
,其中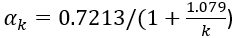 对于 k>128 (为了让采样估测足够准确,k一般需要取数十万,远大于128)。关于 Hyperloglog 算法的具体分析,可以参考原论文 [4]。这一估算过程不需要任何额外空间消耗。
对于 k>128 (为了让采样估测足够准确,k一般需要取数十万,远大于128)。关于 Hyperloglog 算法的具体分析,可以参考原论文 [4]。这一估算过程不需要任何额外空间消耗。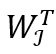 |后,我们还需要用其估算
|后,我们还需要用其估算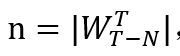 ,注意上文分析中提到,一个子流得到有效样本边的概率
,注意上文分析中提到,一个子流得到有效样本边的概率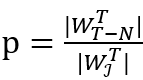 ,而 p 可以通过统计 k 个子流中有效样本的数量来估算, 之后我们用
,而 p 可以通过统计 k 个子流中有效样本的数量来估算, 之后我们用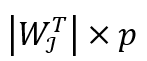 便可以估算出滑动窗口中边的数目。与样本图中的三角形数目 tc 一样,n 也可以被持续记录,我们可以在每次有子流中最大优先级发生变化时对 n 进行修改。
便可以估算出滑动窗口中边的数目。与样本图中的三角形数目 tc 一样,n 也可以被持续记录,我们可以在每次有子流中最大优先级发生变化时对 n 进行修改。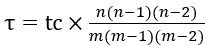 , 我们可以在图流流入的过程中用上述算法持续监视三角形数目的变化。这一计算方式的原因在于,每条边都有相同的概率被加入 m 个样本中,而三角形三条边均被加入样本的概率即为
, 我们可以在图流流入的过程中用上述算法持续监视三角形数目的变化。这一计算方式的原因在于,每条边都有相同的概率被加入 m 个样本中,而三角形三条边均被加入样本的概率即为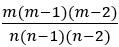 ,这也是每个三角形被加入样本图的概率。我们用样本图中的三角形数目除以这一概率,得到的即为快照图中三角形数目的估计值。
,这也是每个三角形被加入样本图的概率。我们用样本图中的三角形数目除以这一概率,得到的即为快照图中三角形数目的估计值。相比 SIGMOD 会议版本,我们在期刊版本中的最大改进便是提出了异步分组技术(Asynchronous Grouping,简称 AG 技术)。如上文所述,SWTC 算法的样本集大小会随着时间不断波动,在某些时刻会得到较小的样本集合(也就是将要从 Case 2 转为 Case 3 的时候,滑动窗口只有很小一部分和上一个片段相交)。由于在采样估算技术中,样本集的大小直接决定了估算的准确率,较小的样本集合也会导致准确率的下降。为了解决这一问题,我们引入了 AG 技术。
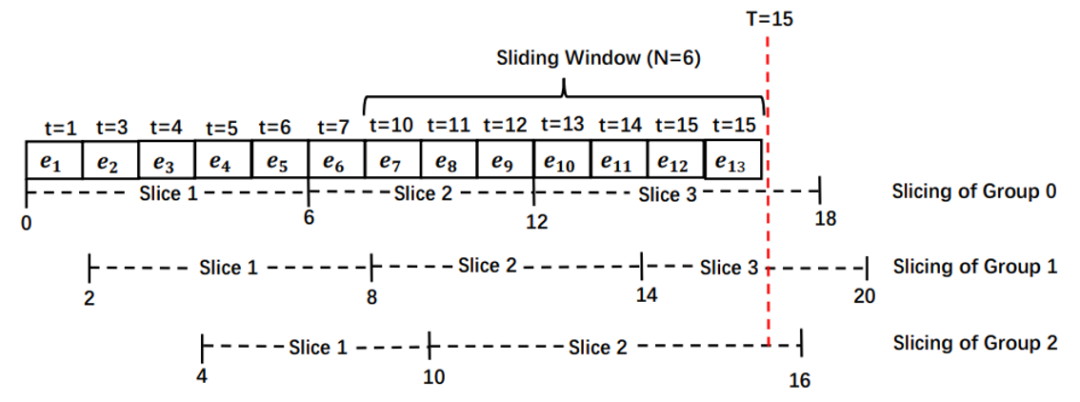
在该技术中,我们把子流分为 g 个组,每组使用不同的路标序列,如图 3所示。具体来,组GPi包含子流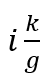 到
到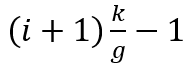 ,而组
,而组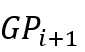 的第 j 个路标比
的第 j 个路标比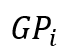 的第 j 个路标大 N/g,而
的第 j 个路标大 N/g,而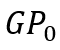 的第一个路标为时刻 0。例如,图 3中的组 1 的第2 个路标是时刻 8,比组 0 的第 2 个路标时刻 6 要大 2。
的第一个路标为时刻 0。例如,图 3中的组 1 的第2 个路标是时刻 8,比组 0 的第 2 个路标时刻 6 要大 2。
每一个组和上述的基础版本的 SWTC 算法同样工作,只是使用自己专有的路标序列。每个组独立计算自己组中互异边数目。最终,我们合并所有组中的样本边得到样本集合,并将所有组中估算出的互异边数目相加得到滑动窗口中的互异边数目。
与基础版本相比,每一个组内的样本集合数目仍然会周期性变化,但是不同组之间的样本数目此消彼长,最终作为一个整体能够保持稳定。我们经过数学分析,得出使用 AG 技术后,样本集合数目仍会波动,但是波动范围缩小到原来的 1/g。
此外,我们在期刊版本中也将我们的算法扩展到了有向三角形计数和局部三角形计数中。前者即为在考虑边方向的情况下的三角形计数,而后者则为估算包含特定点的三角形的数目。进行这两种查询时的方法和上述全局无向三角形计数相同,只需要在样本图中计数时根据不同需求采取不同的计数方法即可。
实验结果
我们的实验分为了二项计数和带权计数两部分。现有工作中缺乏在我们的问题设定下的三角形近似计数算法,因此,二项计数实验中,我们主要和PartitionCT 框架加滑动窗口采样计数BPS 算法 [5] 组合成的 baseline 算法作对比。相比会议版本,我们也增加了和没有空间消耗上限的固定概率采样估算的对比,也就是每一条边到来时以固定概率 p 对其进行采样,采样过程使用哈希算法以过滤重复边。在带权计数中,我们除了和 baseline 对比外,还和已有的两种带权计数算法 WRS [6] 和 ThinkD [7] 作了对比,这两种算法用于含边删除的图流上的三角形计数。与滑动窗口模型不同,这两种算法要求在每次有边删除时,都被明确告知删除边,这使得我们必须要将整个滑动窗口中的边及其时间戳保存下来才能应用这两种算法,这将消耗大量的内存,而且使得内存使用缺乏上限,我们会在实验中看出这样做的弊端。
在数据集选择上,我们在下面实验中主要使用了四个数据集:
StackOverflow: 从StackOverflow论坛上获取的用户交互信息图,点代表用户而边代表用户交互(回答问题,留言等),包含63497050 条边(含重复)和2601977个点。
Yahoo network: 从yahoo 的开源数据集中获取的网络流数据集,点代表IP地址而边表示两个IP之间的通信,包含561754369 条边(含重复)和 33635059 个点。
WikiTalk: 英文维基百科上的用户交流数据,点代表用户,边代表用户之间的交流,包含24,981,163 条边和2,987,535 个点。
Actor:描述演员合作关系的图,点代表演员而每条边表示两个演员之间的一次合作,包含33115812条边(含重复)和382219个点。
前三个数据集包含时间戳信息,而第三个数据集不包含时间戳信息,我们为其中的边随机生成了三组时间戳,计算三次测试的平均值。
在实验参数和测试指标上,我们的baseline 算法和SWTC 算法都只有一个参数 k,且二者具有相同的 k时拥有相同的内存消耗。我们定义采样率 (Sample Rate) 为 k 除以窗口长度,其中窗口长度以图流中数据项到达的平均时间间隔为单位。我们通过改变采样率来控制 k,这样避免了样本过小带来较大误差。注意在应用中窗口长度是不变的,而数据项到达的平均间隔根据历史数据估算即可。因此我们算法在运行时有着明确的空间使用上限,不会随着图流流量改变而改变。我们实验测试的主要指标为相同内存消耗下样本集合的大小和三角形估算的准确率,前者用有效样本集大小 (valid sample size) 来表示,后者用平均相对误差MAPE 和最大误差 MaxError来表示。我们将每个数据集中所有的边按照时间戳顺序提供给算法以模拟图流。每当滑动窗口向前滑动 1/10 时(即算法处理过的边的最大时间戳增加 1/10 N),我们设置一个测试点,测量样本集大小和三角形估测的相对误差 |(τ ̂-τ)/τ| (其中 τ ̂ 表示估算出的三角形数量,而 τ 则为滑动窗口中实际的三角形数量)。最终,我们取所有测试点的相对误差平均值作为 MAPE, 最大值作为最大误差,取样本集大小的平均值作为有效样本集大小。此外,我们使用了5种不同的哈希函数,并计算五组实验的平均值作为最终结果。
图 4展示了baseline 算法和SWTC算法的样本集合大小(SWTC-AG 为使用了AG技术的SWTC 算法)。图 (a) 为在 Actor 上固定采样率为 4% 并改变滑动窗口大小的测试,而图 (b) 为 Yahoo 数据集上固定滑动窗口大小为 35M 而改变采样率的测试。从图中我们可以看出,两种SWTC 算法相比 baseline 算法,在相同条件下有更大的样本大小。其中SWTC-AG 和SWTC 虽然平均样本大小相同,但是 SWTC-AG 的样本大小更稳定,这会在下面的误差测试中表现出来。
图 5展示了baseline 算法和SWTC算法的误差随滑动窗口大小变化的趋势,我们使用了Actor 和 StackOverflow 数据集,采样率设置为 4%。而图 6展示了不同算法的误差随采样率变化的趋势,我们使用了 WikiTalk 和 Yahoo 数据集,滑动窗口大小分别设置为为3M 和 35M。从图中我们可以看出,SWTC 和 SWTC-AG 的 MAPE 相比baseline 算法都具有优势,但是由于 SWTC 算法的样本集大小不稳定,它的最大误差接近 baseline 算法。而SWTC-AG在稳定了样本集大小后,最大误差有了显著下降。
表 1展示了 SWTC 算法和固定概率采样方案的对比。固定概率采样方案虽然简单,但是它的空间占用始终随着图流流量而变化,难以估算。我们使用 WikiTalk 数据集,设置滑动窗口大小为 3M,对 SWTC 算法使用了 4% 的采样率。我们提前处理了一遍数据集,得到滑动窗口中的最大边数,在此基础上,我们为固定概率采样方案设置了两种参数,第一种是设置采样概率使得其最大内存占用,也就是在窗口内边数最多时的内存占用,和 SWTC 一致,也就是表格的第三行。第二种设置则是让两种方法保存相同数目的边。注意 SWTC 在每个子流中保存2条边,所以 SWTC 算法在该设置下始终保存 0.24M 边,我们让固定概率采样最多也保存 0.24M 边,该设置的实验结果在表格第四行。注意第二种设置下,固定概率采样方案的内存使用上限要大于SWTC。从实验结果可以看出,具有相同内存上限的情况下,SWTC和SWTC-AG 都优于固定概率采样,而在保存相同边数时,即使具有更大内存使用上限,固定概率采样也只是和SWTC-AG方案相当。这是由于分配给固定概率采样方案的内存只有在流量峰值会被充分利用,平时难以利用。需要注意的是,实际应用中我们很难提前预知滑动窗口内边数上限,所以固定概率采样会更加难以使用。
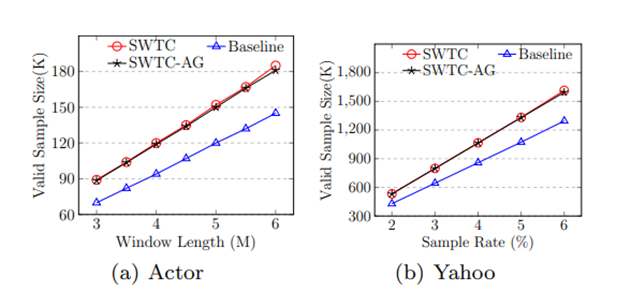
图 4 有效样本集大小测试
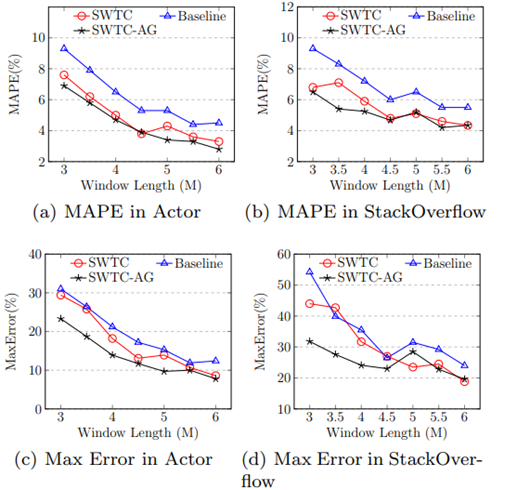
图 5 算法误差随滑动窗口大小变化趋势
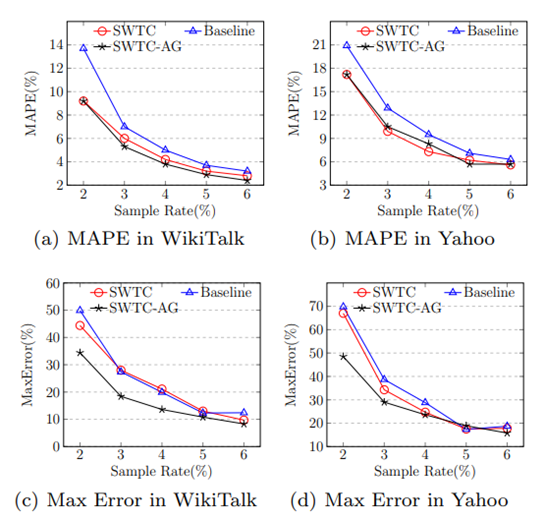
图 6 算法误差随采样率变化趋势
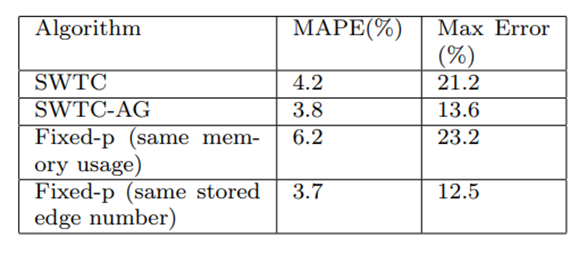
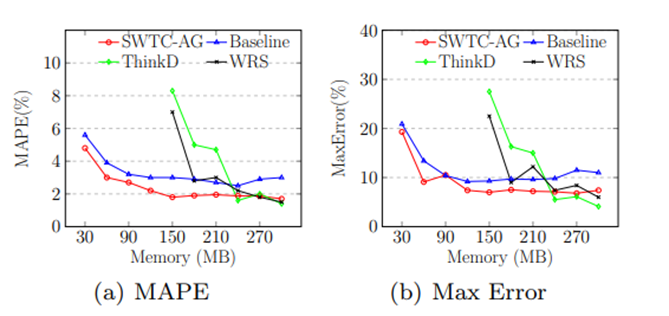
图 7带权计数中各种算法的误差
在带权计数中,我们使用了 StackOverflow 数据集,设置窗口大小为 4.5M, 并改变算法使用的内存来进行实验,结果如图 7所示。如上文所说,WRS 和 ThinkD 算法需要按时序保存滑动窗口内的所有边才能工作。我们统计在整个图流流入的过程中滑动窗口内边数的变化,发现最大为 5.4M。因此 WRS 和 ThinkD 算法至少需要能保存 5.4M 边的空间才能工作,而用单链表按时序保存 5.4 M 边及其时间戳需要 129.6M 空间,因此在图中,这两种算法从150M 内存消耗处才开始具有折线。我们可以看到这两种算法需要至少 210M 内存才能具有 4% 以下的 MAPE, 而baseline 算法和 SWTC 算法只需要 60M 内存就能具有相同的MAPE。此外,在整个折线的变化过程中,SWTC 在相同内存消耗下仍比 baseline 具有更低的MAPE。
更多的实验结果,如无偏性测试,有向三角形计数测试,局部计数测试,速度测试等,请参考我们的论文。
参考文献
[1] Berry J W, Hendrickson B, LaViolette R A, et al. Tolerating the community detection resolution limit with edge weighting[J]. Physical Review E, 2011, 83(5): 056119.
[2] Becchetti L, Boldi P, Castillo C, et al. Efficient algorithms for large-scale local triangle counting[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2010, 4(3): 1-28.
[3] Wang P, Qi Y, Sun Y, et al. Approximately counting triangles in large graph streams including edge duplicates with a fixed memory usage[J]. Proceedings of the VLDB Endowment, 2017, 11(2): 162-175.
[4] Flajolet P, Fusy É, Gandouet O, et al. Hyperloglog: the analysis of a near-optimal cardinality estimation algorithm[C]//Discrete Mathematics and Theoretical Computer Science. Discrete Mathematics and Theoretical Computer Science, 2007: 137-156.
[5] Gemulla R, Lehner W. Sampling time-based sliding windows in bounded space[C]//Proceedings of the 2008 ACM SIGMOD international conference on Management of data. 2008: 379-392.
[6] Lee D, Shin K, Faloutsos C. Temporal locality-aware sampling for accurate triangle counting in real graph streams[J]. The VLDB Journal, 2020, 29(6): 1501-1525.
[7] Shin K, Oh S, Kim J, et al. Fast, accurate and provable triangle counting in fully dynamic graph streams[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2020, 14(2): 1-39.


欢迎关注北京大学王选计算机研究所数据管理实验室微信公众号“图谱学苑“
实验室官网:https://mod.wict.pku.edu.cn/
微信社区群:请回复“社区”获取
gStore官网:http://www.gstore.cn/
GitHub:https://github.com/pkumod/gStore
Gitee:https://gitee.com/PKUMOD/gStore







