2.2.1 矩阵和数组的概念及其区别
对矩阵的基本操作,主要有矩阵的构造、矩阵大小及结构的改变、矩阵下标引用、矩阵信息的获取等。对于这些操作,MATLAB中都有固定指令或相应的库函数与之相对应。
在数学上,定义由m×n个数aij(i=1,2,…,m; j=1,2,…,n)排成的m行n列的数表
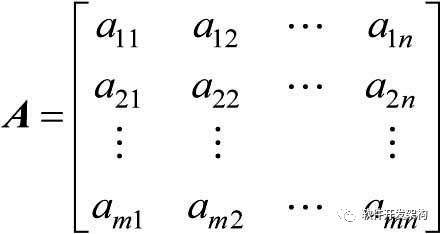
为m行n列矩阵,并用大写黑体字母表示它。
只有一行的矩阵
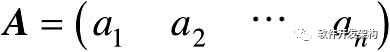
称为行向量。
同理,只有一列的矩阵

称为列向量。
矩阵最早来自方程组的系数及常数所构成的方阵,这一概念由19世纪英国数学家凯利首先提出。数组是在程序设计中,为了处理方便,把具有相同类型的若干变量按有序的形式组织起来的一种形式。这些按序排列的同类数据元素的集合称为数组。
在MATLAB中,一个数组可以分解为多个数组元素,这些数组元素可以是基本数据类型或构造类型。因此,按数组元素的类型不同,数组又可分为数值数组、字符数组、单元数组、结构数组等。
由此可见,矩阵和数组在MATLAB中存在很多方面的区别,主要有以下几个方面:
● 矩阵是数学上的概念,而数组是计算机程序设计领域的概念。
● 作为一种变换或者映射运算符的体现,矩阵运算有着明确而严格的数学规则;而数组运算是MATLAB软件定义的规则,其目的是使数据管理方便,操作简单,命令形式自然,执行计算有效。
两者间的联系主要体现在:在MATLAB中,矩阵是以数组的形式存在的。因此,一维数组相当于向量,二维数组相当于矩阵,所以矩阵是数组的子集。
2.2.2 矩阵的构造
矩阵的构造方式有两种,一种与单元数组相似,可以对变量直接进行赋值;另一种是使用MATLAB中提供的构造特殊矩阵的函数,如表2-12所示。
表2-12 特殊矩阵的构造函数
函数名称 | 函数功能 |
ones(n) | 构建一个n×n的1矩阵(矩阵的元素全部是1) |
ones(m,n,…,p) | 构建一个m×n×…×p的1矩阵 |
ones(size(A)) | 构建一个和矩阵A同样大小的1矩阵 |
zeros(n) | 构建一个n×n的0矩阵(输出矩阵的元素全部是0) |
zeros(m,n,…,p) | 构建一个m×n×…×p的0矩阵 |
zeros(size(A)) | 构建一个和矩阵A同样大小的0矩阵 |
eye(n) | 构建一个n×n的单位矩阵 |
eye(m,n) | 构建一个m×n的单位矩阵 |
eye(size(A)) | 构建一个和矩阵A同样大小的单位矩阵 |
magic(n) | 构建一个n×n的矩阵,其每一行、每一列的元素之和都相等 |
rand(n) | 构建一个n×n的矩阵,其元素为0~1之间均匀分布的随机数 |
rand(m,n,…,p) | 构建一个m×n×…×p的矩阵,其元素为0~1之间均匀分布的随机数 |
randn(n) | 构建一个n×n的矩阵,其元素为零均值、单位方差的正态分布随机数 |
randn(m,n,…,p) | 构建一个m×n×…×p的矩阵,其元素为零均值、单位方差的正态分布随机数 |
diag(x) | 构建一个n维的方阵,它的主对角线元素值取自向量x,其余元素的值都为0 |
diag(A,k) | 构建一个由矩阵A第k条对角线的元素组成的列向量 k = 0为主对角线;k < 0为下第k条对角线;k > 0为上第k条对角线 |
diag(x,k) | 构建一个(n+|k|)×(n+|k|)维的矩阵,该矩阵的第k条对角线元素取自向量x,其余元素都为0(关于参数k,参考上个命令) |
triu(A) | 构建一个和A大小相同的上三角矩阵,该矩阵的主对角线上元素为A中相应元素,其余元素都为0 |
triu(A,k) | 构建一个和A大小相同的上三角矩阵,该矩阵的第k条对角线及其以上元素为A中相应元素,其余元素都为0 |
tril(A) | 构建一个和A大小相同的下三角矩阵,该矩阵的主对角线上元素为A中相应元素,其余元素都为0 |
tril(A,k) | 构建一个和A大小相同的下三角矩阵,该矩阵的第k条对角线上及其以下元素为A中相应元素,其余元素都为0 |
1.建立简单矩阵
简单矩阵采用矩阵构造符号——方括号“[]”,将矩阵元素置于方括号内,同行元素之间用空格或逗号隔开,行与行之间用分号“;”隔开,格式如下:
matrixName = [element11, element12, element13; element21, element22, element23]
matrixName = [element11 element12 element13; element21 element22 element23]
例2-31:简单矩阵构造示例。
分别构造一个二维矩阵、一个行向量、一个列向量。在命令行窗口中依次输入:
A = [2,3,5;3,6,10] % 使用逗号和分号构造二维矩阵
B = [2 3 5;3 6 10] % 使用空格和分号构造二维矩阵
V1 = [8,59,60,33] % 构造行向量
V2 = [5;8;3;4;9] % 构造列向量
程序运行过程中的输出如下:
A =
2 3 5
3 6 10
B =
2 3 5
3 6 10
V1 =
8 59 60 33
V2 =
5
8
3
4
9
2.建立特殊矩阵
特殊矩阵是指非零元素或零元素的分布有一定规律的矩阵,常见的特殊矩阵有对称矩阵、三角矩阵和对角矩阵等。
例2-32:特殊矩阵构造示例。
在命令行窗口中输入:
OnesMatrix = ones(2),ZerosMatrix = zeros(2),Identity = eye(2),Identity23 = eye(2,3),Identity32 = eye(3,2)
输出结果:
OnesMatrix =
1 1
1 1
ZerosMatrix =
0 0
0 0
Identity =
1 0
0 1
Identity23 =
1 0 0
0 1 0
Identity32 =
1 0
0 1
0 0
在命令行窗口中输入:
Random = rand(2,3),Array = Random(:,2),Diagelement = diag(Random),Diagmatrix = diag(diag(Random)),Dmatrix_array = diag(Array),UpperTriangular = triu(Random),LowerTriangular = tril(Random)
输出结果:
Random =
0.0975 0.5469 0.9649
0.2785 0.9575 0.1576
Array =
0.5469
0.9575
Diagelement =
0.0975
0.9575
Diagmatrix =
0.0975 0
0 0.9575
Dmatrix_array =
0.5469 0
0 0.9575
UpperTriangular =
0.0975 0.5469 0.9649
0 0.9575 0.1576
LowerTriangular =
0.0975 0 0
0.2785 0.9575 0
3.向量、标量和空矩阵
通常情况下,矩阵包含m行n列,即m×n。当m和n取一些特殊值时,得到的矩阵具有一些特殊的性质。
(1)向量。
当m=1或n=1,即1×n或m×1时,建立的矩阵称为向量。例如输入:
a = [1 2 3 4 5 6]
b = [1;2;3;4;5;6]
whos % 调用whos函数查看变量a、b的相关信息
得到结果:
a =
1 2 3 4 5 6
b =
1
2
3
4
5
6
Name Size Bytes Class Attributes
a 1x6 48 double
b 6x1 48 double
(2)标量。
当m=n=1时,建立的矩阵称为标量。任意以1×1的矩阵形式表示的单个实数、复数都是标量。
例2-33:在MATLAB中,标量有两种表示方法。例如,在命令行窗口中依次输入:
x = 10 + 2i % 将复数10 + 2i赋值给变量x
shape = size(x) % 查询变量x的形状信息
y = [10 + 2i] % 将复数10 + 2i构成的矩阵赋值给变量y
shape = size(y) % 查询变量y的形状信息
x == y % 判断变量x和y是否相等,“1”表示相等,“0”表示不相等
得到结果:
x =
10.0000 + 2.0000i
shape =
1 1
y =
10.0000 + 2.0000i
shape =
1 1
ans =
logical
1
通过上述示例可知,单个实数或复数在MATLAB中都是以矩阵的形式存储的;在MATLAB中,单个数据或由单个数据构造的矩阵都是标量。
(3)空矩阵。
当m=n=0,或者m=0,或者n=0,即0×0、0×n、m×0时,创建的矩阵称为空矩阵。空矩阵可以通过赋值语句建立。例如输入:
x = [] % 建立一个空矩阵
whos x % 调用whos函数查看变量x的相关信息
得到结果:
x =
[]
Name Size Bytes Class Attributes
x 0x0 0 double
而再建立一个0矩阵,可以输入:
z = [0 0 0;0 0 0] % 建立一个2行3列的0矩阵
whos z % 调用whos函数查看变量z的相关信息
得到结果:
z =
0 0 0
0 0 0
Name Size Bytes Class Attributes
z 2x3 48 double
空矩阵和0矩阵的本质区别在于:空矩阵内没有任何元素,因此不占用任何存储空间;而0矩阵表示该矩阵中的所有元素全部为0,需要占用一定的存储空间。
2.2.3 矩阵大小及结构的改变
根据运算时的不同情况和需要,矩阵大小及结构的改变方式主要有旋转矩阵、改变矩阵维度、删除矩阵元素等。MATLAB中提供的具体此类函数如表2-13所示。
表2-13 矩阵旋转与改变维度的函数
函数名称 | 函数功能 |
fliplr(A) | 矩阵每一行均进行逆序排列 |
flipud(A) | 矩阵每一列均进行逆序排列 |
flipdim(A,dim) | 生在一个在dim维矩阵A内的元素交换位置的多维矩阵 |
rot90(A) | 生成一个由矩阵A逆时针旋转90°而得到的新矩阵 |
rot90(A,k) | 生成一个由矩阵A逆时针旋转k×90°而得到的新矩阵 |
reshape(A,m,n) | 生成一个m×n×维的矩阵,其元素以线性索引的顺序从矩阵A中取得 如果矩阵A中没有m×n×个元素,将返回一条错误信息 |
repmat(A,[m n …p]) | 创建一个和矩阵A有相同元素的m×n×…×p块的多维矩阵 |
shiftdim(A,n) | 矩阵的列移动n步。n为正数,矩阵左移;n为负数,矩阵右移 |
squeeze(A) | 返回没有空维的矩阵A |
cat(dim,A,B) | 将矩阵A和B组合成一个dim维的多维矩阵 |
permute(A,order) | 根据向量order来改变矩阵A中的维数顺序 |
ipermute(A,order) | 进行命令permute的逆变换 |
sort(A) | 对一维或二维矩阵进行升序排序,并返回排序后的矩阵 当A为二维矩阵时,对矩阵的每一列分别进行排序 |
sort(A,dim) | 对矩阵按指定的方向进行升序排序,并返回排序后的矩阵。当dim = 1时,对矩阵的每一列排序;当dim = 2时,对矩阵的每一行排序 |
sort(A,dim,mode) | 当mode为'ascend'时,进行升序排序; 当mode为'descend'时,进行降序排序; |
[B,IX] = sort(A,…) | IX为排序后备元素在原矩阵中的行位置或列位置的索引 |
例2-34:矩阵的旋转与维度的改变。
在命令行窗口中输入:
Randoma = randn(1,4),Randomb = randn(2),Randoma = reshape(Randoma,2,2),Randoma = fliplr(Randoma),Randoma = rot90(Randoma),Randomc = cat(2,Randoma,Randomb)
输出结果:
Randoma =
3.0349 0.7254 -0.0631 0.7147
Randomb =
-0.2050 1.4897
-0.1241 1.4090
Randoma =
3.0349 -0.0631
0.7254 0.7147
Randoma =
-0.0631 3.0349
0.7147 0.7254
Randoma =
3.0349 0.7254
-0.0631 0.7147
Randomc =
3.0349 0.7254 -0.2050 1.4897
-0.0631 0.7147 -0.1241 1.4090







