二叉排序树的插入和删除操作

梁霖编程工具库 2023-01-12

681

二叉排序树介绍

二叉排序树是一棵二叉树或者空树
若它的左子树不空，则左子树的所有节点的关键字均小于根节点
若它的右子树不空，则右子树的所有节点的关键字均大于根节点

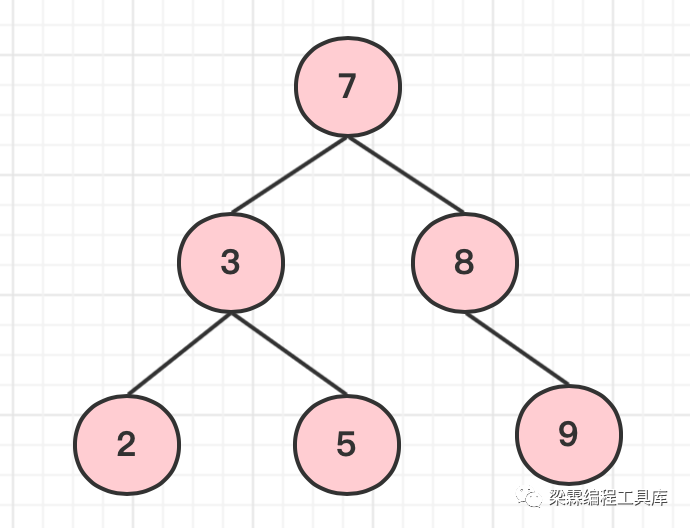
二叉排序树的插入操作

插入操作是指向一个二叉排序树中插入一个元素，如果这个元素已经存在，则插入失败；如果不存在则插入成功。
插入操作结束后仍旧需要保证这个二叉排序树的左小右大的特点。
比如向上面这个二叉排序树中插入元素6，这个元素6最后会插入在节点5的右孩子处。

插入操作——代码实现

// 返回true代表插入成功，返回false代表插入失败
    public boolean insert(BTNode p){
        if(p==null){
            return false;
        }
        if(root==null){
            root = p;
        }else{
            //工作节点
            BTNode work = root;
            while(work!=null){
                if(work.val < p.val){
                    //p应该插入在work的右边
                    if(work.right!=null){
                        work = work.right;
                    }else{
                        //完成了插入;
                        work.right = p;
                        break;
                    }
                }else if(work.val > p.val){
                    //p应该插入在work的左边
                    if(work.left != null){
                        work = work.left;
                    }else{
                        //完成插入插入操作
                        work.left = p;
                        break;
                    }
                }else{
                    //我们找到了一个一抹一样的节点,更新info信息，返回fasle
                    work.info = p.info;
                    return false;
                }
            }
        }
        return true;
    }

二叉排序树的查询操作

查询操作就是从树的根节点出发，查找知道关键值的元素，如果可以找到则返回这个元素，如果不可以找到则返回空。

查询操作的代码实现

public BTNode find(int val){
        BTNode p = root;
        while(p!=null){
            if(p.val == val){
                break;
            }else if(p.val < val){
                //说明目标节点在p的右边
                p = p.right;
            }else{
                //说明目标节点在p的左边
                p = p.left;
            }
        }
        return p;
    }

二叉排序树的删除操作

删除操作是指需要在一棵二叉排序树中删除指定关键字的节点，同样的删除以后需要保证二叉排序树的左小右大的特征。

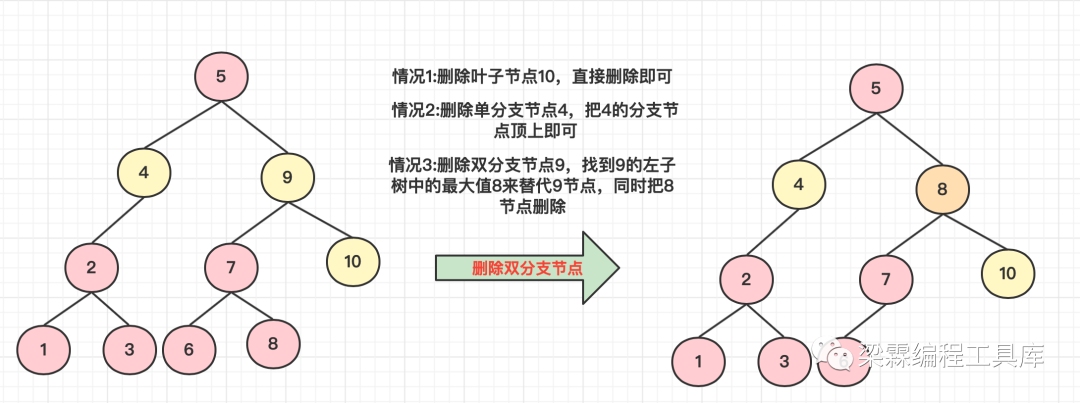
二叉排序树删除的三种情况

删除的是叶子节点，即待删除元素左右子树都为空的情况，直接删除即可。
删除的是单分支的节点，即待删除元素左子树为空右子树不为空或者右子树为空左子树不为空，只需要讲其孩子节点来替代这个待删除的节点即可。
删除的是双分支节点，即待删除的元素左右子树都不空的情况，可以将其左子树中的最大值来替换当前节点，同时删除左子树中的最大值，或者可以将其右子树中的最小值来替换当前节点，同时删除右子树中的最小值。

删除节点的时候，我们需要找到待删除目标节点的父节点，比如下图中我们需要删除节点4，我们需要找到4的父节点5，让5的左指针指向2。

删除操作代码实现

public boolean delete(int val){
        //1、先找到待删除元素的父节点
        BTNode target = findDel(val);
        if(target==null){
            // 说明查找失败
            return false;
        }
        //2、删除元素 ---> 根节点  非根节点
        //左子树的最大值来填充
        if(val == root.val){
            //说明删除的是根节点
            if(root.left == null && root.right ==null){
                root = null;
            }else if(root.left == null){
                root = root.right;
            }else if(root.right == null){
                root = root.left;
            }else{
                //寻找左子树最大值
                BTNode p = root.left;
                while(p.right != null){
                    p = p.right;
                }
                delete(p.val);
                root.val = p.val;
                root.info = p.info;
            }
        }else{
            //说明删除的不是根节点,则target是待删除元素的父亲节点
            if(target.left!=null && target.left.val == val){
                //说明需要删除的是target的左节点
                BTNode del = target.left;
                if(del.left == null && del.right == null){
                    target.left = null;
                }else if(del.left == null){
                    target.left = del.right;
                }else if(del.right == null){
                    target.left = del.left;
                }else{
                    //说明待删除元素有左右孩子节点
                    BTNode p = del.left;
                    while(p.right!=null){
                        p = p.right;
                    }
                    delete(p.val);
                    del.val = p.val;
                    del.info = p.info;
                }
            }else{
                //说明待删除的是target的右孩子
                BTNode del = target.right;
                if(del.left == null && del.right == null){
                    target.right = null;
                }else if(del.left == null){
                    target.right = del.right;
                }else if(del.right == null){
                    target.right = del.left;
                }else{
                    //说明待删除元素有左右孩子节点
                    BTNode p = del.left;
                    while(p.right!=null){
                        p = p.right;
                    }
                    delete(p.val);
                    del.val = p.val;
                    del.info = p.info;
                }
            }
        }
        return true;
    }


    //找的是val的父节点
    public BTNode findDel(int val){
        if(root==null){
            return null;
        }
        if(val == root.val){
            return root;
        }
        BTNode p = root;
        while(p!=null){
            if(val < p.val){
                if(p.left != null && p.left.val == val){
                    return p;
                }else if(p.left == null){
                    return null;
                }else{
                    //存在但不相等
                    p = p.left;
                }
            }else{
                if(p.right !=null && p.right.val == val){
                    return p;
                }else if(p.right == null){
                    return null;
                }else{
                    p = p.right;
                }
            }
        }
        return null;
    }

二叉排序树的不足

假设我们需要建立一棵二叉排序树，但我们依次插入的元素是[1，2，3，4，5，6，7，8，9），那么我们实际插入的树其实以一颗只有右子树，没有左子树的树。那么其查找效率会退化为一个单链表。‍‍‍‍‍‍‍

二叉排序树 target

文章转载自梁霖编程工具库，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

二叉排序树的插入和删除操作

评论