图的遍历算法

梁霖编程工具库 2023-01-06

351

图的基本介绍

图是由节点有穷集合V和边的集合E组成，一个图中至少有一个节点，但边可以有也可以没有。
图可以分为有向图和无向图，有向图中的边都是有方向的，无向图中的边时没有方向的。
在图中，边是用于表示两个节点之间的一种关系，通常会用两个定点表示边。比如在有向图中<A,D>边表示由节点A出发到达节点D的边，在无向图中(A,D)边表示链接A和D的边，这条边既可以由A到D，也可以由D到A。

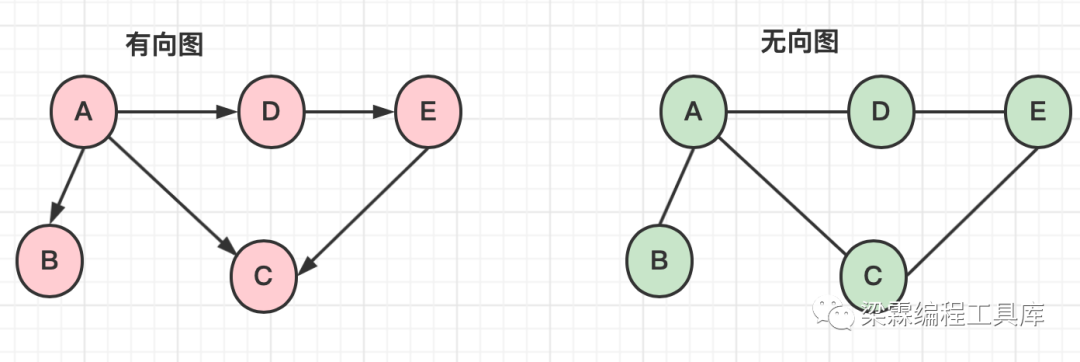
边的入度和出度

节点的度是用于表示由多少条边与这个节点相关联，比如在有向图中节点A的度为3，表示有3条边与节点A相关联。
节点的入度是用于表示有多少条边指向这个节点，比如在有向图中节点A的入度为0，节点C的入度为2。
节点的出度是用于表示有多少条边从这点节点发出，比如在有向图中节点A的出度为3，节点C的出度为0。

有向完全图和无向完全图

有向完全图：若有向图中有n个节点，且图中任意两个节点都有两条反向的边链接，即一共有n*(n-1)条边，则称之为有向完全图。
无向完全图：若无向图中有n个节点，且图中任意两节点之间都有一条边链接，即一共有n*(n-1)/2条边，则称之为无向完全图。
‍‍

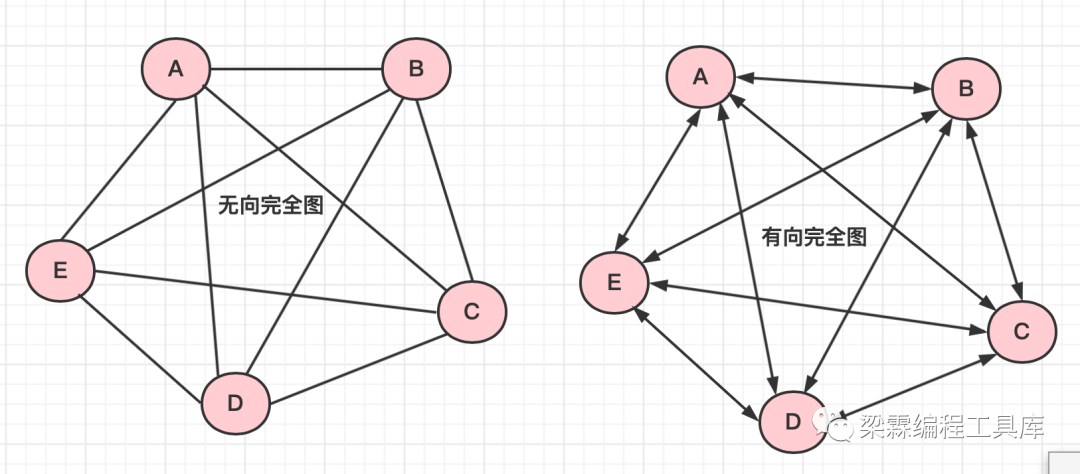
路径

路径是相邻顶点序偶所构成的序列称之为路径，比如上图的有向图中<A,D>、<D,E>、<E,C>就构成一条路径，表示从A可以到达D，再到达E，最后到达C。

连通、连通图和连通分量

节点A和节点B之间存在一条路径，则称节点A和节点B之间是连通的，也称之为节点A 可达节点B
连通图是指从图中的任意节点出发，都可以达到其余的所有节点，则将该图称之为连通图。
连通分量是指从图中取部分节点和部分边，若所取的这些节点和边构成的图是连通的，则将这部分节点和边组成的集合称之为原图的一个连通分量。

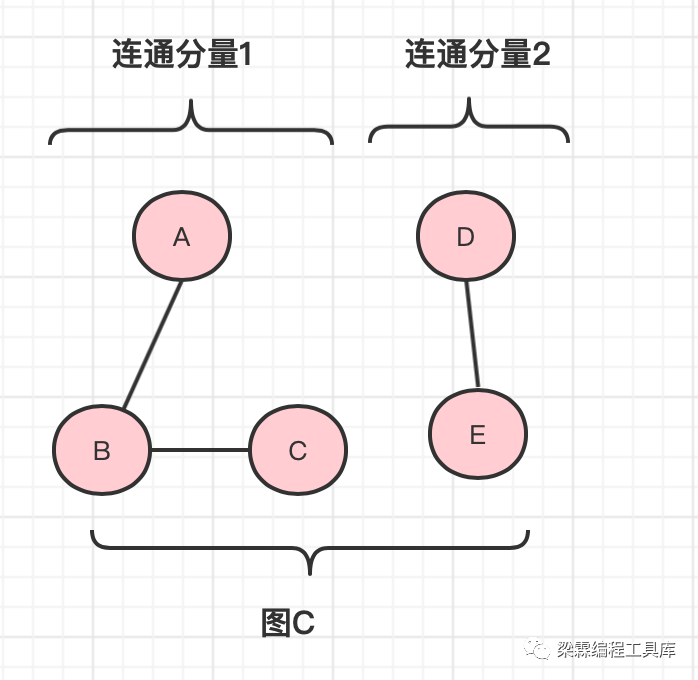
权和网

如果图中每条边都带上一个相应的数字，这种与边相关的数称之为权，权可以用于表示一个节点到另一个节点到距离或者代价。
边上带有权重的图也称之为带权图，或者称之为网。

图的存储结构——邻接矩阵的介绍

邻接矩阵是表示节点之间关系的矩阵，假设图G={V,E}是一个有n个节点的图，节点的编号是从0～n-1，则我们定义的图G的邻接矩阵A是有如下特性的方阵：

A(i,j) = 0 ,表示节点i 不存在一条直接指向 节点j 的边
‍‍
A(i,j) = 1 ,表示节点i 存在一条直接指向 节点j 的边

如果图中的边是带权重的，那么我们可以将图G定义为：

A(i,j) = w ,表示节点i 存在一条直接指向 节点j 的边，且边的权重为w
A(i,j) = INF，INF为无穷大 ,表示节点i 不存在一条直接指向 节点j 的边

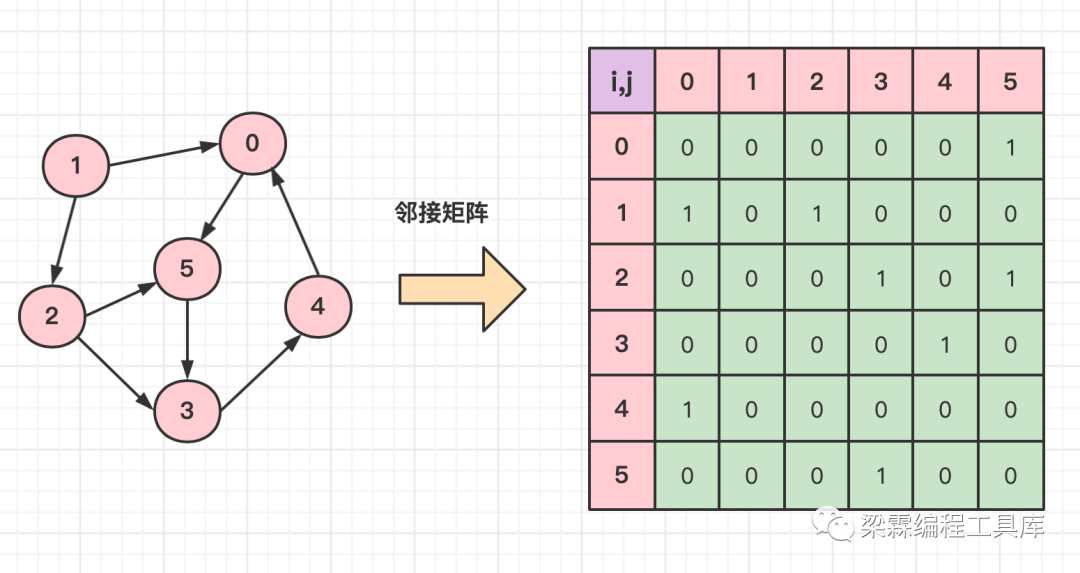
邻接矩阵代码实现

/**
 * 定义节点信息
 */
class Vertex{
    public int no; //节点编号
    public String info; //节点的其他信息
    public Vertex(int no,String info){
        this.no = no;
        this.info = info;
    }
}


/**
 * 定义邻接矩阵
 */
public class MatricGraph {
    public Vertex[] vertices;
    public int[][] matric;
    public MatricGraph(int n,int[][] edges){
        vertices = new Vertex[n];
        matric = new int[n][n];
        for(int i=0;i<n;i++){
            vertices[i] = new Vertex(i,String.valueOf(i));
        }
        for(int k=0;k<edges.length;k++){
            int i = edges[k][0];
            int j = edges[k][1];
            matric[i][j]=1;
        }
    }


    /**
     * 输出邻接矩阵
     */
    public void output(){
        for(int i=0;i<matric.length;i++){
            for(int j=0;j<matric[0].length;j++){
                System.out.printf("%d \t",matric[i][j]);
            }
            System.out.println();
        }
    }
}


//Main函数启动类
public class Main {
    public static void main(String[] args) {
        int[][] edges = new int[][]{{1,0},{1,2},{2,5},{2,3},{5,3},{3,4},{4,0},{0,5}};
        MatricGraph graph = new MatricGraph(6,edges);
        graph.output();
    }
}

图的存储结构——邻接表的介绍

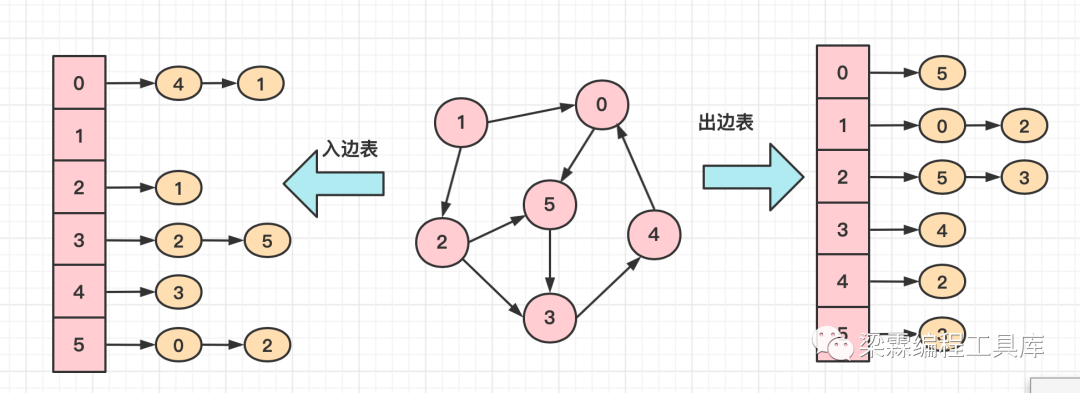
邻接表是图的一种链式存储结构，邻接表的表头用于存放节点信息，每个节点后面用单链表连接着该节点的所有邻居节点。
邻接表是由节点表和边表组成，针对无向图，边表就是与节点相连接的边；针对有向图，边表若是从该节点发出的边则称之为出边表，边表若是指向该节点的边则称之为入边表。
如果图是一个带权图，可以在每个边节点上增加一个带权因子，用于表示权重。

邻接表代码实现

/**
 * 边表的节点
 */
class EdgeNode{
    public int no; //节点编号
    public EdgeNode next; // 下一个边
    public EdgeNode(int no){
        this.no = no;
        next = null;
    }


    @Override
    public String toString() {
        return "EdgeNode{" +
                "no=" + no +
                '}';
    }
}


/**
 * 节点表的节点
 */
class VertexNode{
    public int no; //节点编号
    public String info; // 节点额外信息
    public EdgeNode neighbors; // 邻居节点
    public VertexNode(int no,String info){
        this.no = no;
        this.info = info;
        neighbors = null;
    }


    @Override
    public String toString() {
        return "VertexNode{" +
                "no=" + no +
                ", info='" + info + '\'' +
                '}';
    }
}
/**
 * 定义邻接表 [出边表]
 */
public class LinkGraph {
    public VertexNode[] graph;
    /**
     *传入节点个数n和边信息edges ,edges[k] = {i，j} 表示从i到j有一条边
     */
    public LinkGraph(int n,int[][] edges){
        graph = new VertexNode[n];
        for(int i=0;i<n;i++){
            graph[i] = new VertexNode(i,String.valueOf(i));
        }
        for(int k=0;k<edges.length;k++){
            int i = edges[k][0];
            int j = edges[k][1];
            EdgeNode edgeNode = new EdgeNode(j);
            //采用头插入法
            edgeNode.next = graph[i].neighbors;
            // 当前节点neighbors就是邻居节点
            graph[i].neighbors = edgeNode;
        }
    }


    public void output(){
        for(int i=0;i< graph.length;i++){
            System.out.println("节点 "+graph[i].toString()+" 的邻居：");
            EdgeNode edgeNode = graph[i].neighbors;
            while(edgeNode!=null){
                System.out.printf("%s \t" , edgeNode);
                edgeNode = edgeNode.next;
            }
            System.out.println();
        }
    }
}


public class Main {
    public static void main(String[] args) {
        int[][] edges = new int[][]{{1,0},{1,2},{2,5},{2,3},{5,3},{3,4},{4,0},{0,5}};
        LinkGraph graph = new LinkGraph(6,edges);
        graph.output();
    }
}

图的遍历算法——深度优先遍历（DFS）介绍

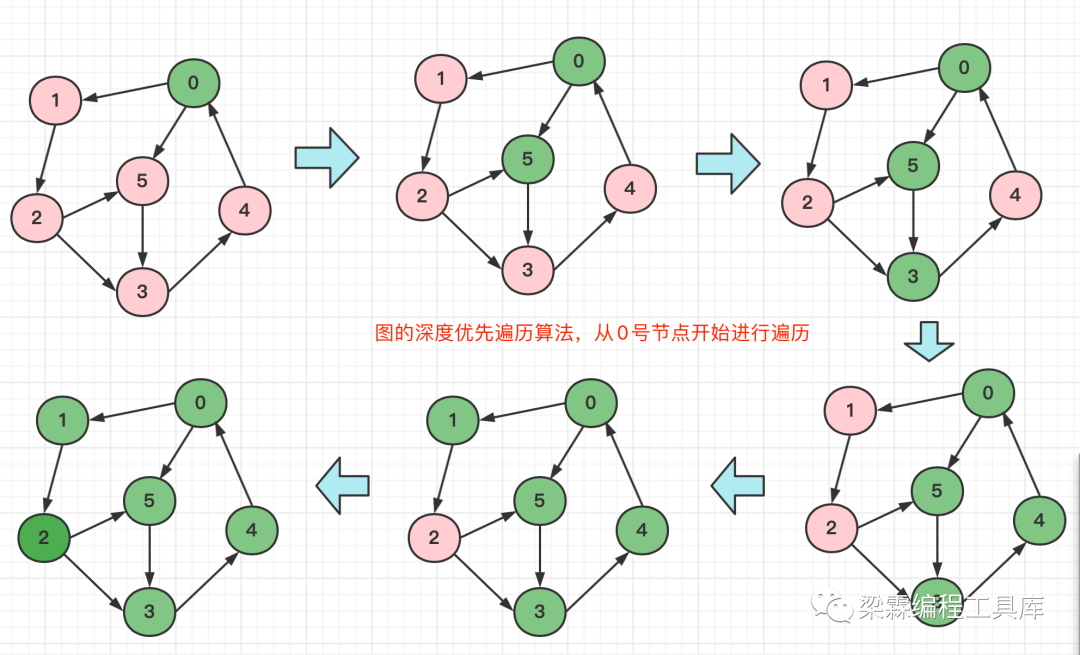
图的深度优先遍历思路：从访问出发点v开始，将v标记为已访问过，然后选取v的所有邻居节点，从这些没有被访问过的邻居节点出发，继续访问。

基于邻接表的DFS代码实现

 /**
     * 图的深度优先遍历
     */
    public void dfs(int i,boolean[] isVisited){
        System.out.println(graph[i]);
        isVisited[i] = true;
        EdgeNode neighbor = graph[i].neighbors;
        while(neighbor!=null){
          //只要存在邻居且邻居没有访问过，就对这个进行进行dfs
            if(!isVisited[neighbor.no]){
                dfs(neighbor.no,isVisited);
            }
            neighbor = neighbor.next;
        }
    }
    
public class Main {
    public static void main(String[] args) {
        int[][] edges = new int[][]{{0,1},{1,2},{2,5},{2,3},{5,3},{3,4},{4,0},{0,5}};
        LinkGraph graph = new LinkGraph(6,edges);
        graph.output();
        boolean[] isVisited = new boolean[6];
        graph.dfs(0,isVisited);
    }
}

算法性能分析

深度优先遍历是针对每一个节点，访问了该节点的每一条边一次，因此我们可以假设一共有n个节点，有e条边，所以算法的时间复杂度的上限是O(n*e)

图的遍历算法——广度优先遍历（BFS）介绍

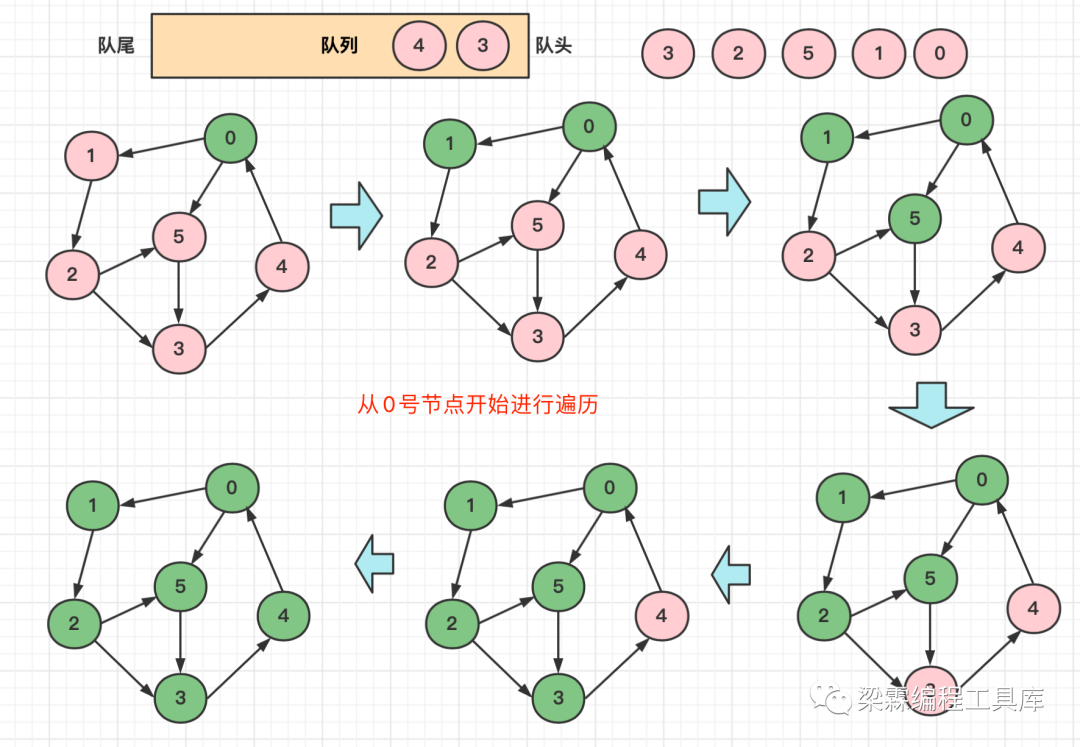
图的广度优先遍历的基本思路：首先访问起始节点v，然后依次访问节点v的邻居节点w1，w2，w3，... ,然后再继续访问w1的邻居节点，w2的邻居节点,.....，这样反复访问，直到访问结束。
可以发现广度优先遍历是需要利用一个队列来实现的，下面我们给出广度优先遍历的流程图。

基于邻接表的BFS代码实现

  /**
     * 图的广度优先遍历
     */
    public void bfs(){
        Queue<Integer> queue = new LinkedList<>();
        boolean[] isVisited = new boolean[graph.length];
        //队列初始化
        queue.offer(0);
        //遍历
        while(!queue.isEmpty()) {
            int cur = queue.poll();
            if(!isVisited[cur]) {
                System.out.println(graph[cur]);
                isVisited[cur] = true;


                EdgeNode edgeNode = graph[cur].neighbors;
                while (edgeNode != null) {
                    if (!isVisited[edgeNode.no]) {
                        queue.offer(edgeNode.no);
                    }
                    edgeNode = edgeNode.next;
                }
            }
        }
    }
    
    
public class Main {
    public static void main(String[] args) {
        int[][] edges = new int[][]{{0,1},{1,2},{2,5},{2,3},{5,3},{3,4},{4,0},{0,5}};
        LinkGraph graph = new LinkGraph(6,edges);
        graph.output();


        System.out.println("图的广度优先遍历");
        graph.bfs();
    }
}

‍‍‍

string

文章转载自梁霖编程工具库，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

图的遍历算法

评论