提出问题
现在假设我们有一个有向带权图,请计算出从某一节点出发,到达其他节点中路径之和最小的哪条路径。
迪杰斯特拉算法介绍
设有两个顶点集合S和T,集合S中存放的是图中已经找到的最短路径的节点,T集合中存放的是图中还没有确定最短路径的节点。初始状态下,S集合中只包含源点v0,然后不断从集合T中选取已知的最短路径的节点加入到S集合中,当T集合为空时,整个算法就结束。
迪杰斯特拉算法涉及三个辅助数组dist[],path[],set[]
dist[i] :表示从源点出发到达第 i 号节点 的最短距离。
path(i) = j : 表示到达第 i 号节点的最短距离是从 第 j 号节点到达的。
set(i) = 0 表示第i号节点的最短距离还没有确定, set(i) = 1 表示第i号节点的距离已经确定了。
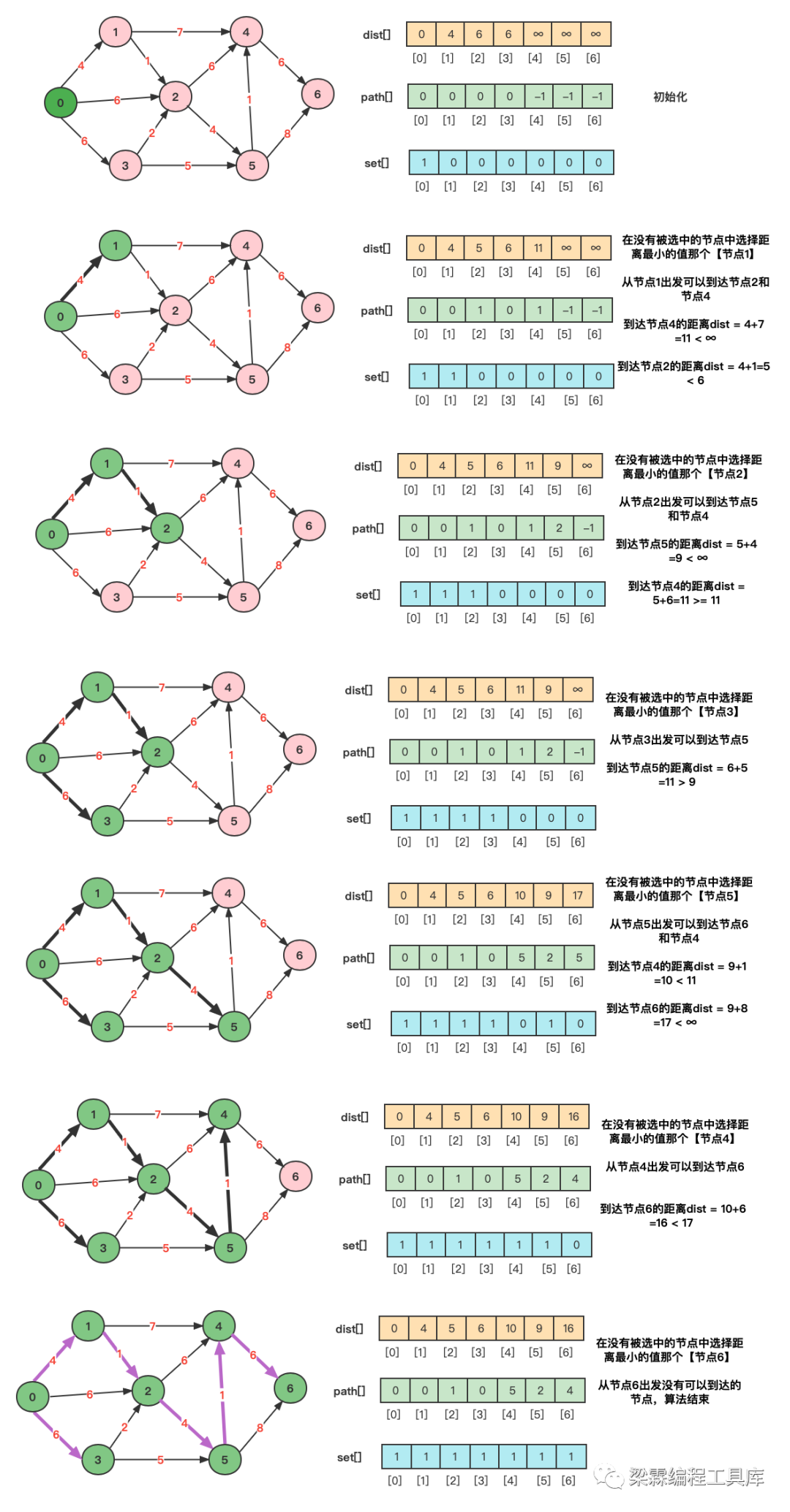
图解迪杰斯特拉算法
基于邻接表的代码实现
/*** 边表的节点*/class EdgeNode{//节点编号public int no;// 权重public int weight;// 下一个边public EdgeNode next;public EdgeNode(int no,int weight){this.no = no;this.weight = weight;next = null;}@Overridepublic String toString() {return "EdgeNode{" +"no=" + no +'}';}}public class LinkedGraph {public EdgeNode[] graph;public int dist[];public int path[];public int set[];public LinkedGraph(int n,int[][] edge){graph = new EdgeNode[n];for(int i =0;i<edge.length;i++){int first = edge[i][0];int second = edge[i][1];// 权重int weight = edge[i][2];EdgeNode node = new EdgeNode(second,weight);/*** graph[first]本身就是first的一个邻居节点*/if(graph[first] == null){graph[first] = node;}else{node.next = graph[first];graph[first] = node;}}}/*** 从k出发,得到最短路径*/public void dijkstra(int k){int n = graph.length;dist = new int[n];path = new int[n];set = new int[n];//初始化for(int i=0;i<n;i++){dist[i] = Integer.MAX_VALUE;path[i] = -1;set[i] = 0;}dist[k] = 0;path[k] = 0;set[k] = 1;// 更新k的邻居节点update(k);int cnt = 1;// 正式执行dijstra主体代码while(cnt < n){//选择最小距离的节点int nodeIdx = selectMinDist();if(nodeIdx==-1){break;}set[nodeIdx] = 1;cnt++;// 更新dist,pathupdate(nodeIdx);}}/*** 选择距离最小且还没有被确定最短距离的节点* @return*/private int selectMinDist(){int min = -1;for(int i=0;i<dist.length;i++){if(set[i]==0){if(min == -1){min = i;}else if(dist[i]< dist[min]){min = i;}}}return min;}/*** 从k节点出发,更新dist和path*/private void update(int k){EdgeNode neighbor = graph[k];while(neighbor!=null){if(set[neighbor.no]==0){int newDist = dist[k]+neighbor.weight;if(newDist < dist[neighbor.no]){dist[neighbor.no] = newDist;path[neighbor.no] = k;}}neighbor = neighbor.next;}}}//Main函数 调用public class Main {public static void main(String[] args) {// {0,1,4} 表示从0 到 1 存在一条权重为4的边int[][] edge = new int[][]{{0,1,4},{0,3,6},{0,2,6},{1,2,1},{1,4,7},{2,4,6},{2,5,4},{3,2,2},{3,5,5},{4,6,6},{5,4,1},{5,6,8}};LinkedGraph graph = new LinkedGraph(7,edge);graph.dijkstra(0);System.out.println("dist数组");for(int i=0;i<graph.dist.length;i++){System.out.printf("%d \t",graph.dist[i]);}System.out.println();System.out.println("path数组");for(int i=0;i<graph.path.length;i++){System.out.printf("%d \t",graph.path[i]);}System.out.println();}}
算法性能分析
dijkstra算法时间复杂度分析:整个算法的外层while循环要走n次,每次循环都要选择最小的节点,这个选择的过程也是n次,总体的时间复杂度是O(n*n),n为节点的个数。
关于迪杰斯特拉算法的后续思考
在选择最小值的过程中, 不论这个节点是否加入了set集合都会被遍历一边,但如果这个节点已经被加入到了set集合中的时候就可以被排除了,因此在这个选择的过程中我们可以借鉴堆排序的思路进行优化。
文章转载自梁霖编程工具库,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






