大量浮点时间序列数据正以前所未有的高速率生成。一种高效、紧凑、无损的时间序列数据压缩方法对海量数据的应用场景至关重要。现有的大多数浮点无损压缩方法是基于异或操作，但它们没有充分利用尾随零，这通常会导致压缩率不尽如人意。本次为大家带来重庆大学START团队在数据库领域顶级会议VLDB 2023最新收录的论文《Elf: Erasing-based Lossless Floating-Point Compression》。
一．背景
传感设备和物联网的发展带来了时间序列数据的爆炸增长。例如，波音787上的传感器每次飞行可以产生高达0.5 TB的数据。这些庞大的浮点时间序列数据如果以原始格式传输和存储，将占用大量的网络带宽和存储空间，降低系统效率。
一种有效的方法是在传输和存储之前对时间序列数据进行压缩。通用压缩算法如LZ4和Xz，虽然可以达到很好的压缩率，但没有利用时间序列数据的内在特征，而且他们只能按照批处理模式运行，非常耗时，且不太适合流式时间序列数据。针对流式浮点时间序列数据的压缩方法有两类，即有损压缩算法和无损压缩算法。但有损压缩算法会丢失一些信息，不适合科学计算、数据管理、网络传输等关键场景。针对流式浮点数据的无损压缩通常基于异或运算，典型的算法如Gorilla和Chimp。Gorilla假设连续两个浮点值的XOR结果很可能有许多前导零和尾随零。但据我们统计大多数情况下，XOR结果只有很少的尾随零，如图1所示。
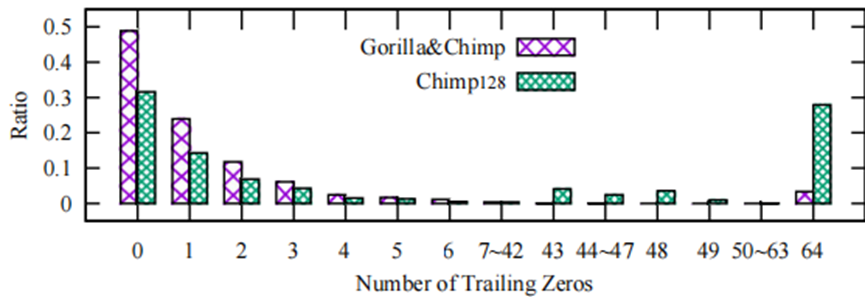
图1 尾随零数量统计
为了增加XOR结果的尾随零的数量，我们提出了一种基于擦除的无损浮点压缩算法𝐸𝑙𝑓。𝐸𝑙𝑓的基本思想是通过擦除浮点值的最后几位(即设置为零)，获得一个带有大量尾随零的XOR结果。𝐸𝑙𝑓面临三个挑战：（1）如何快速确定被擦除的位；（2）如何无损地恢复原始浮点数据；（3）如何压缩擦除的浮点数据。通过严格的理论分析，𝐸𝑙𝑓可以快速确定被擦除的位，并在没有任何精度损失的情况下恢复原始浮点值，如图2所示。针对大量尾随零的XOR结果，论文提出了一种详细的编码策略，进一步提高压缩性能。
图2 ELF擦除和恢复示例
二．方法介绍
2.1 总体框架
图3显示了𝐸𝑙𝑓算法的总体框架，由擦除器、压缩器、解压器和恢复器组成。在压缩过程中，尽可能多地擦除数据vi的尾随零，由此可以得到一个擦除值v’i，并使用少量比特对XOR结果Δ
进行编码。解压缩过程相当于压缩的逆过程，根据Δ和解压得到的擦除值v’i，可以无损恢复原数据vi。
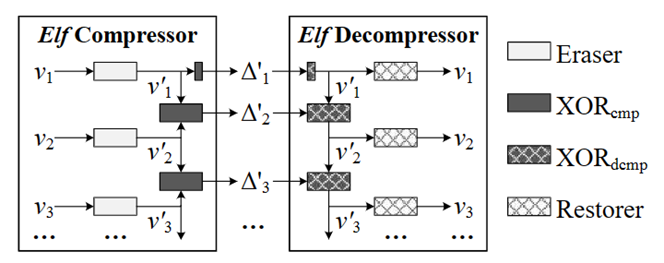
图3 总体框架图
2.2定义
（1）先导零、尾随零和中心位：如图4所示，先导零为XOR结果Δ的底层格式中，第一个1之前的所有零；尾随零为Δ最后一个1之后的所有零；中心位为先导零和尾随零之间的数据。
图4 基于XOR压缩方式的实例
（2）小数位数、十进制有效计值位数和十进制有效值起始位置：给定𝑣的十进制格式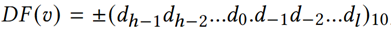
，小数位数𝐷𝑃(𝑣) = |𝑙|；dn-1是第一位不等于0的，则𝑆𝑃(𝑣) = 𝑛−1称为十进制有效值起始位置；十进制有效值位数𝐷𝑆(𝑣) = 𝑛−𝑙 = 𝑆𝑃(𝑣)+1−𝑙。例如𝐷𝑃 (3.14) = 2, 𝐷𝑆 (3.14) = 3, 𝑆𝑃 (3.14) = 0; 𝐷𝑃 (−0.0314) = 4, 𝐷𝑆 (−0.0314) = 3, 𝑆𝑃 (−0.0314) = −2; 𝐷𝑃 (314.0) = 1, 𝐷𝑆 (314.0) = 4, 𝑆𝑃 (314.0) = 2.
（3）尾数前缀数MPN（Mantissa Prefix Number）：一个双精度浮点数𝑣有尾数部分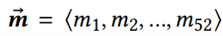
，另有双精度浮点数𝑣’有尾数部分
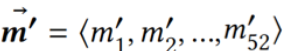，若𝑣’尾数前半部分与𝑣相同，尾数后半部分全为零，则称𝑣为𝑣的尾数前缀数。
2.3 Elf擦除器
给定一个双精度值𝑣，其十进制格式为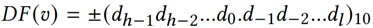
，我们可以找到它的一个尾数前缀𝑣’和一个很小的双精度值𝛿，0≤𝛿<10α，使得𝑣’=𝑣−𝛿。如果保留𝑣’和𝛿的信息，可以不损失任何精度地恢复𝑣。
一方面，一个数可以有多个尾数前缀。论文的目标是最大化XOR结果的尾随零数量，故选择具有最多尾随零的最优尾数前缀。
另一方面，𝛿的计算和存储可以省略。若𝛿≠0并且十进制小数位数𝐷𝑃(𝑣)已知，假设𝛼=𝐷𝑃(𝑣)和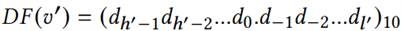
,我们有
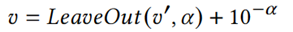
其中是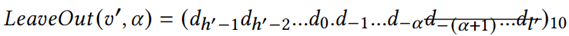
在𝐷F(𝑣’)中省略d-α后的数字。𝛿=0表示𝑣本身有很长的尾随零，因此不进行擦除操作。
（1）尾数前缀搜索：无论是迭代查找还是改进的二分查找，其时间复杂度都较大。论文提出了一种新的尾数前缀的搜索方法，该方法只需要O(1)的时间复杂度。
定理1：
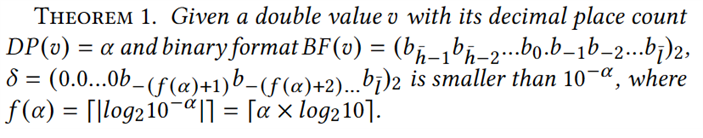
其中，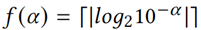
意味着十进制数10-α正好需要𝑓(𝛼)位之后的二进制数来近似表示。根据论文的定理1，𝑣−𝛿可以认为是在𝑣的二进制格式𝐵𝐹(𝑣)中擦除b-f(α)后面的位。又由IEEE754格式可知，一个双精度浮点数的二进制格式中小数点后的每一位，均能与IEEE754格式中的尾数部分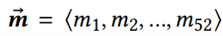一一对应，且公式为
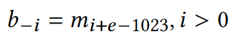，其中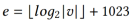
。故𝐵𝐹(𝑣)中b-f(α)对应IEEE754格式中m-g(α)，且
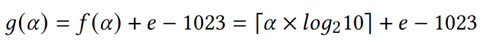
因此，通过擦除双精度值𝑣的底层格式m-g(α)之后的数，可以快速获得最优尾数前缀𝑣’。
（2）小数位数计算：IEEE754标准下，最小的双精度浮点数表示为4.9×10-324，故直接存储𝛼= 𝐷𝑃(𝑣)需要9bits。实际上，双精度浮点数能精确表示的十进制数的有效值位数𝛽= 𝐷𝑆(𝑣) ≤ 17，且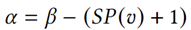
，因此存储𝛽能减少比特数使用。
定理2：
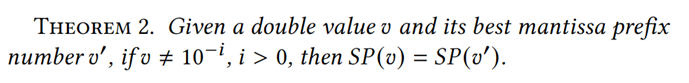
定理3：
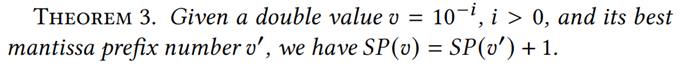
根据论文中的定理2和定理3，可以在未知原始值𝑣的情况下求得小数位数𝛼：
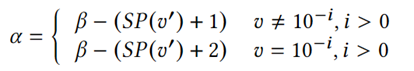
又v=10-i等价于v=10SP(v)，𝑣可以通过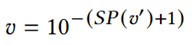
直接求得。
此处修正十进制有效值位数𝛽为𝛽*：
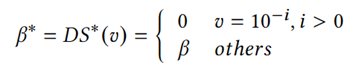
𝛽*∈{0,1,2,…,17}，有18种取值。根据以下
定理4：
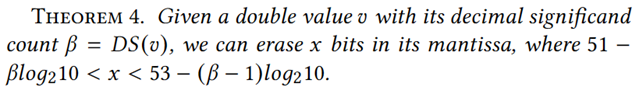
可知被擦除位数𝑥依赖于𝛽。若𝛽≤14，至少可以擦除⌈51−14×log210⌉= 5位，保证了正增益；若𝛽≥16，最多只能擦除⌊53−(16−1)×log210⌋= 3位，导致负增益。因此，不考虑𝛽*= 16或17的情况，利用4bits来记录 𝛽*。
为了保证增益为正，当𝛽= 𝐷𝑆(𝑣) ≥ 16且52 − 𝑔(𝛼) ≤ 4（被擦除位数小于等于4位）时，不进行擦除操作。
故𝑣的恢复总结为
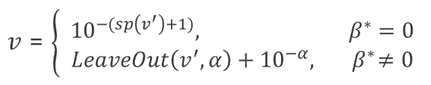
其中𝛼 = 𝛽*- (SP(v’)+1)。
（2）擦除算法：算法1给出了尾数擦除过程的伪代码。算法使用1bit作为标志来指示是否擦除了𝑣，将双精度值𝑣和输出流𝑜𝑢𝑡作为输入。首先，计算小数位数𝛼和修正后的有效值位数𝛽*，并通过提取𝑣的最后52 − 𝑔(𝛼)位尾数位得到𝛿。
如果这三个条件同时成立(即:𝛽* < 16，𝛿≠ 0和52 − 𝑔(𝛼) > 4)，则输出流𝑜𝑢𝑡写入1位𝑓𝑙𝑎𝑔“1”，然后写入4位的𝛽*作为𝑣的恢复使用。通过擦除𝑣的最后52 − 𝑔(𝛼)位尾数得到𝑣。否则，输出流𝑜𝑢𝑡写入1位𝑓𝑙𝑎𝑔“0”，不做任何修改将𝑣’赋值为𝑣。
最后，获得的𝑣’与𝑜𝑢𝑡一起传递给基于XOR的压缩器进行进一步压缩。
2.4 Elf恢复器
𝐸𝑙𝑓恢复器是𝐸𝑙𝑓擦除器的逆过程。算法2描述了𝐸𝑙𝑓恢复器的伪代码，它接受一个输入流𝑖𝑛。首先，从输入流𝑖𝑛中读取1bit来获得修改标志𝑓𝑙𝑎𝑔，它有两种情况：
(1)如果𝑓𝑙𝑎𝑔等于0，则没有修改原始值，因此从基于XOR的解压器中获取一个值并将其直接赋值给𝑣；
(2)否则，我们从输入流𝑖𝑛中读取4bits得到修正后的有效值位数𝛽*，然后从基于XOR的解压器中得到一个值𝑣。如果𝛽* = 0，𝑣 = 10-(sp(v' )+1)；． 如果𝛽* ≠ 0，根据算法中等式(7)和等式(4)从𝛽*和𝑣’中恢复𝑣。
最后，返回恢复的𝑣。
2.5 Elf压缩器
由于被擦除的值v’往往包含长尾零，为了压缩时间序列，论文提出了一种新的基于XOR的压缩器和相应的解压器。
第一个值的压缩：经擦除后v’1有大量的尾随零，利用⌈log265⌉= 7位来记录v’1尾随零𝑡𝑟𝑎𝑖𝑙的位数，并以64-𝑡𝑟𝑎𝑖𝑙位存储v’1的非尾随零部分，总计使用71-𝑡𝑟𝑎𝑖𝑙位来记录第一个值，这通常小于64位。
其他值的压缩：论文提出的基于XOR的压缩器是在Gorilla的基础上扩展的，同时借鉴了Chimp的一些思想。
（1）Gorilla压缩器：如图5(a)所示，如果xort = 0 (即v’t = v’t-1)，写1位“0”,不再存储v’t。如果xort ≠ 0，写1位“1”，进一步检查条件C1：leadt≥ leadt-1 与 trailt ≥ trailt-1是否满足（即xort的前导零位数和尾随零位数均大于或等于xort-1）。如果C1不成立，再写一位“1”，并分别用5bits和6bits存储前导零位数和中心位位数，然后是实际的中心位数据。否则，xort与xort-1共享前导零位数和中心位位数。
（2）前导零优化：由于XOR值的前导零位数很少大于30或小于8，Chimp仅使用3位来表示最多24个前导零，即用0、8、12、16、18、20、22、24来近似表示前导零位数。如果实际的前导零位数在0到7之间，Chimp将其近似为0，以此类推。因此C1条件转化为C2：leadt= leadt-1 与 trailt ≥ trailt-1。将此优化应用于Gorilla压缩器，如图5(b)所示。
（3）中心位优化：XOR值通常具有较长的尾随零和前导零，而中心位不超过16位。因此，如果中心位位数小于或等于16，使用log216 = 4位对其进行编码。相比原始解决方案，通常可以节省一个比特。如图5(c)所示。
（4）标志位重分配：前面只使用1位标志位来表示xort = 0的情况，但对于xort ≠ 0的情况，使用了2或3位标志位。但在浮点时间序列中，相同的连续值并不常见，仅使用1位来表示xort = 0的情况并不是特别有效。如图5(d)所示，为每个情况重新分配了标志位。
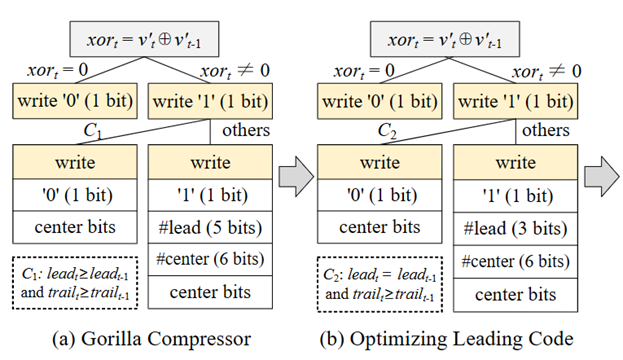
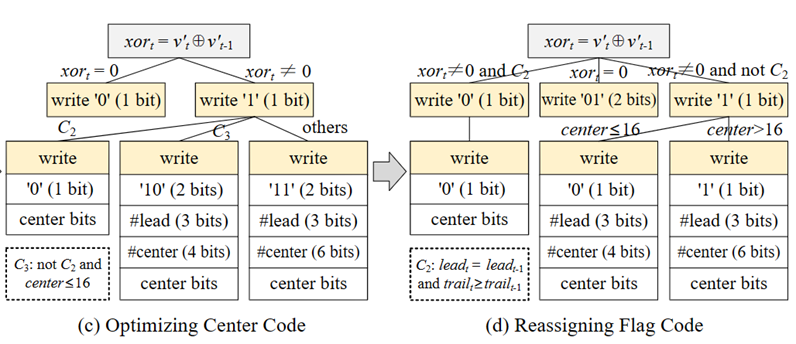
图5 对v’t(𝑡≠1)进行𝐸𝑙𝑓XOR𝑐𝑚𝑝的优化过程
算法3描述了𝐸𝑙𝑓XOR𝑐𝑚𝑝的伪代码。在第1-4行中，处理时间序列的第一个值，在第6-22行中，分别处理图5(d)所示的四种情况。
2.6 Elf解压器
解压缩的过程和与压缩相反。如算法4所示，解压器𝐸𝑙𝑓 XOR𝑑𝑐𝑚𝑝以输入流𝑖𝑛作为输入，在第1-3行中解压缩第一个值，并在第5-17行中分别处理四种不同情况。
对于case01，算法将当前值v’t设置为先前值v’t-1。对于case 00、case 10和case 11，首先更新前导零位数leadt和中心位位数𝑐𝑒𝑛𝑡𝑒𝑟，从而求得当前值v’t。最后，返回v’t到𝐸𝑙𝑓恢复器。
三．实验
论文采用22个数据集，包括14个时间序列和8个非时间序列，并根据平均十进制有效值位数𝛽分为大、中、小三类。
论文将𝐸𝑙𝑓压缩算法与四种无损浮点压缩方法(Gorilla、Chimp、Chimp128和FPC)和五种通用压缩方法(Xz、Brotli、LZ4、Zstd和Snappy)进行了比较。并通过将𝐸𝑙𝑓擦除器作为预处理步骤，比较了Gorilla、Chimp和Chimp128的三个变体算法，以验证擦除和XOR𝑐𝑚𝑝策略的有效性。
此外，论文从压缩率、压缩时间和解压时间这三个指标来验证各种算法的性能。
3.1 压缩率
从图6实验结果观察可知，相比无损浮点压缩算法，𝐸𝑙𝑓在几乎所有的数据集上都有最好的压缩率，无论是时间序列数据集，还是非时间序列数据集，其中对于时间序列数据集，𝐸𝑙𝑓的压缩率相对于Gorilla和FPC平均相对提高了51%，并分别比Chimp和Chimp128获得47%和12%的相对改善；𝐸𝑙𝑓与通用压缩算法在压缩率上旗鼓相当，甚至相比LZ4和snappy有明显优势；而对于large 𝛽的数据集，所有压缩算法的压缩率均不理想。
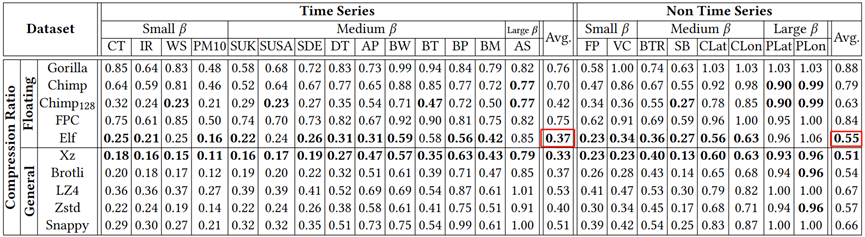
图6 压缩率比较
3.2 压缩时间与解压时间
观察图7实验数据，可以发现通用压缩算法的平均压缩时间比浮点压缩算法多一到两个数量级，因此无法应用于实际场景；𝐸𝑙𝑓在压缩和解压缩过程中都比其他浮点压缩算法花费了更多的时间，增加了一个擦除步骤和一个恢复步骤，但压缩时间和解压时间都在同一个数量级上，差异并不明显。
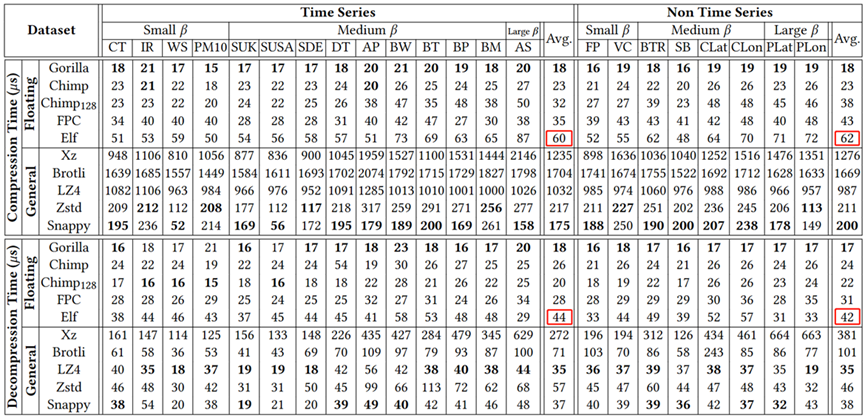
图7 压缩时间与解压时间比较
3.3 𝐸𝑙𝑓相比Chimp128的效率提升
考虑一个数据传输场景：假设原始数据大小为𝐷，压缩率为𝜂，压缩速率、解压缩速率、传输速率分别为rcmp、rdcmp、rtr。数据收发的总延时时间为𝑡 =D/rcmp + D/rdcmp + 𝐷×𝜂/rtr 。由上述数据可得
故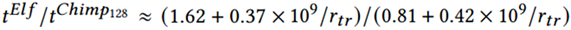
，当传输速率rtr小于6.17 × 107bits/s时，𝐸𝑙𝑓的总体性能优于Chimp128。在典型的CS架构中，一个连接的带宽很少超过6.17 ×107bits/s，且对于每个连接，Chimp128将分配33KB的内存，这对于高并发场景是负担不起的。
3.4 不同𝛽值的性能表现
为了进一步研究𝛽的影响，通过逐步减少时间序列数据集AS和非时间序列数据集PLon的十进制有效值位数𝛽进行了一组实验，并选择Chimp128和Snappy作为基准。
如图8所示，𝛽在3和13之间时，𝐸𝑙𝑓总是保持最好的压缩率。当𝛽= 6时，𝐸𝑙𝑓相对于Chimp128和Snappy的压缩率增益最高。对于不同的𝛽，𝐸𝑙𝑓的压缩时间比Chimp128稍长，但比Snappy短得多。虽然𝐸𝑙𝑓的解压时间大约是Chimp128的两倍，但始终小于60𝜇s。
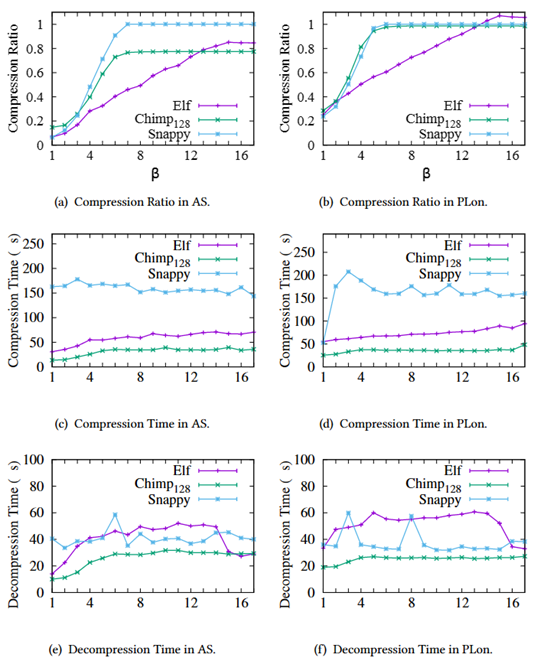
图8 不同𝛽的性能表现
3.5 验证擦除和XOR𝑐𝑚𝑝策略
为了验证擦除策略的有效性，我们将𝐸𝑙𝑓擦除器作为对Gorilla、Chimp和Chimp128的预处理操作。
如图9所示，对于𝛽较小或中等的数据集，擦除策略都可以显著提高Gorilla和Chimp的压缩率，但Chimp128几乎不能从擦除策略中受益。对于𝛽较大的数据集，𝐸𝑙𝑓擦除器不能增强基于XOR的压缩器的压缩率。
在𝛽不是很大的情况下，𝐸𝑙𝑓压缩算法比经过𝐸𝑙𝑓擦除器优化过的Gorilla和Chimp算法甚至提高了8.7% ~ 33.3%，由此验证了XOR𝑐𝑚𝑝优化策略的有效性。
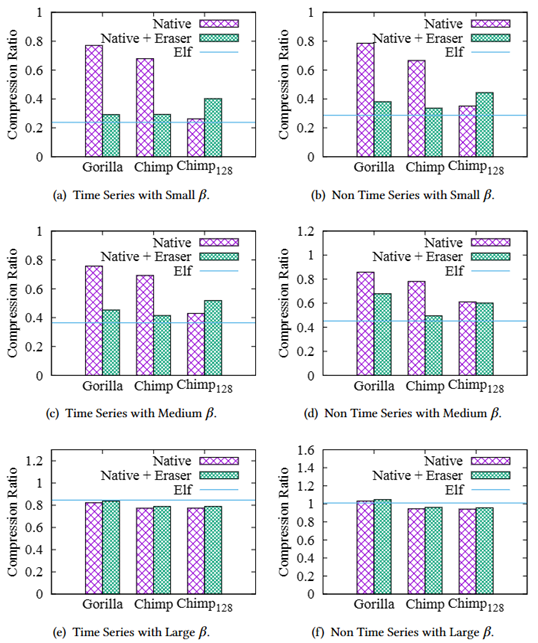
图9 擦除和XOR𝑐𝑚𝑝策略对压缩率的提升
四．总结
本文介绍了𝐸𝑙𝑓，一种新颖、紧凑、高效的基于擦除的流式浮点类型无损压缩算法。使用22个数据集的大量实验验证了𝐸𝑙𝑓的强大性能。实验结果表明，𝐸𝑙𝑓比Chimp128和Gorilla的平均相对压缩率分别提高了12.4%和43.9%。此外，𝐸𝑙𝑓具有与最好的通用压缩算法相似的压缩率，而所需的时间要少得多。
-End-
本文作者 朱明辉 重庆大学计算机科学与技术专业准研究生，重庆大学START团队成员。主要研究方向：时空数据挖掘 |
|
时空艺术团队（START，Spatio-Temporal Art）来自重庆大学时空实验室，旨在发挥企业和高校的优势，深入探索时空数据收集、存储、管理、挖掘、可视化相关技术，并积极推进学术成果在产业界的落地！年度有2~3名研究生名额，欢迎计算机、GIS等相关专业的学生报考！
