数据流处理已成为计算机科学领域的基础之一,在数据库、数据挖掘、安全等方面都有着重要的应用。在流处理中,一个重要的问题是判断数据是否存在于数据流中,而越旧的数据往往价值越低,因此,为更新的数据提供更高的查询精确度是值得的。本次为大家带来数据库领域顶级会议ICDE的论文:《The Stair Sketch: Bringing more Clarity to Memorize Recent Events》
数据流处理包括数据的采集分析以及关于当前或之前数据的查询。具体而言,给定一个数据流以及一个时间段[T1, T2 ],人们往往对一个对象是否出现在数据流中,或者出现过多少次感兴趣。然而,并不是所有数据的重要程度是相等的,人们往往关心最近的事情更多一些。比如Youtube推荐系统根据点击量对视频的流行程度进行排名,尤其是最近的点击量。由于如今的数据流吞吐量大,通常采用称为sketch的次线性数据结构来进行数据查询,因为它们的查询效率和空间占用都非常优秀,布隆过滤器就是一种典型的sketch。本文接下来均以布隆过滤器为例进行介绍。鉴于最近发生的事情的重要性以及sketch的高效率,论文旨在设计一种新的sketch,它可以为最新的数据提供更高的查询准确度。这种特性称之为时间渐进性,主要包括两个方面:- 错误渐进性:论文的方案对最近的时期进行查询时更准确,这方便更好地利用内存。
- 时间稳定性:最近过去的估计误差需要稳定在一个明确定义的范围内。这保证了该方案的长期部署和使用。
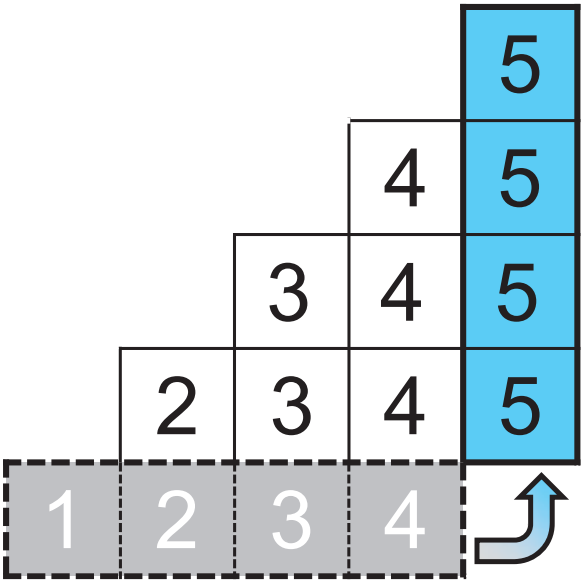
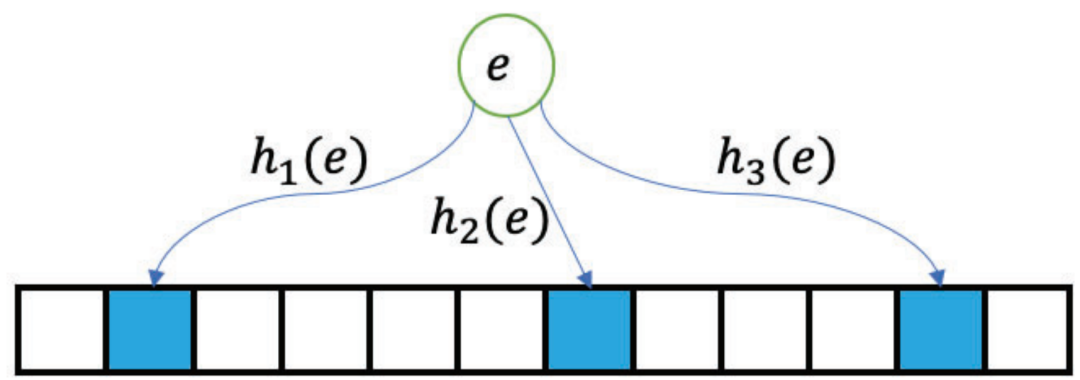
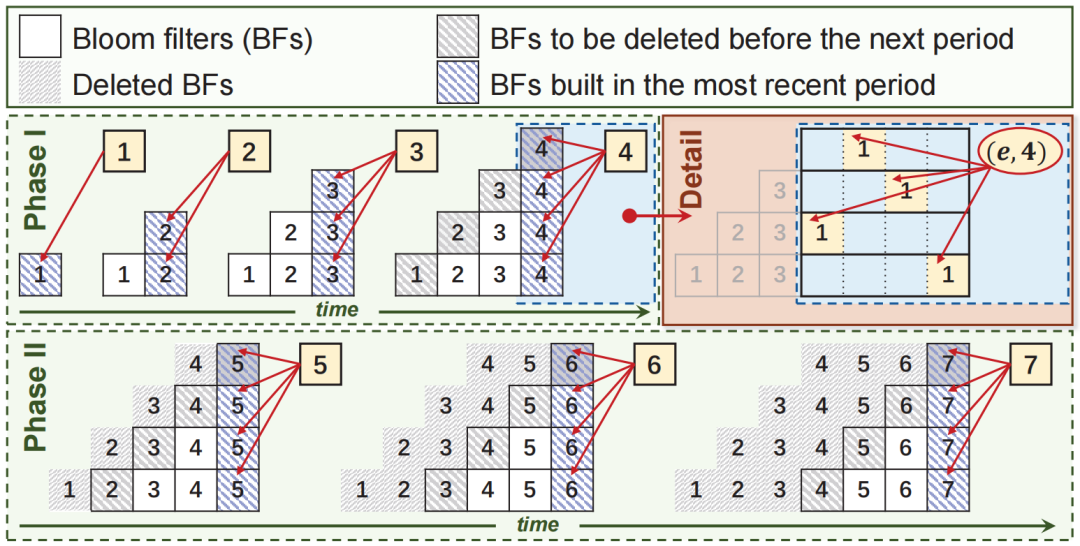
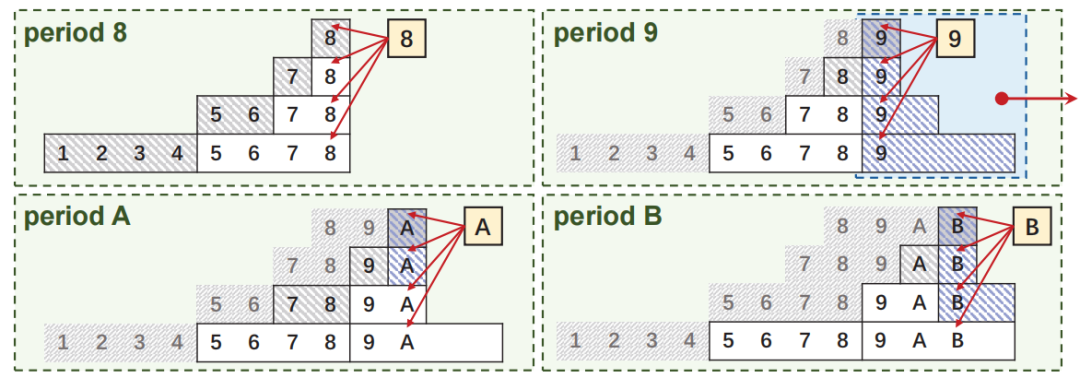
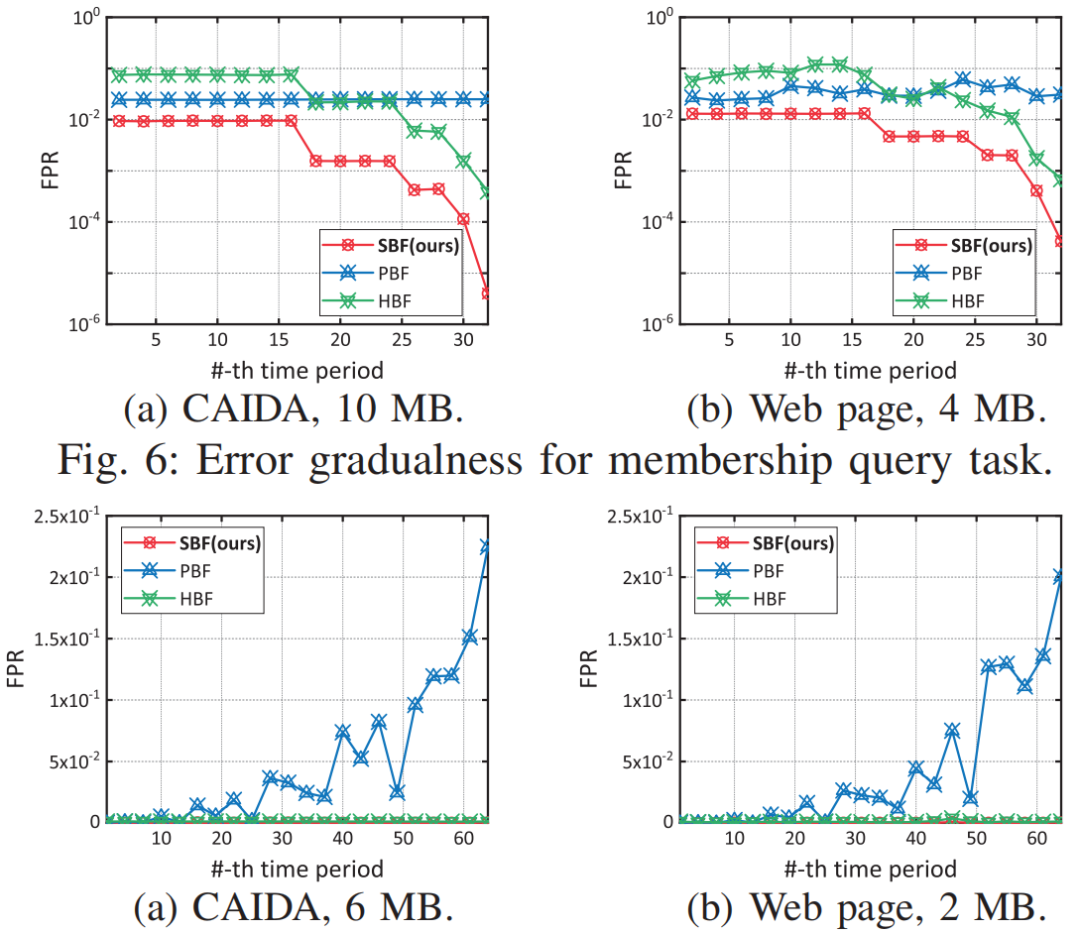
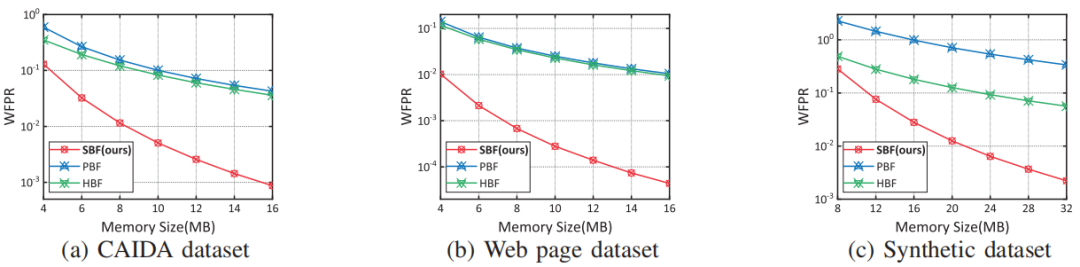
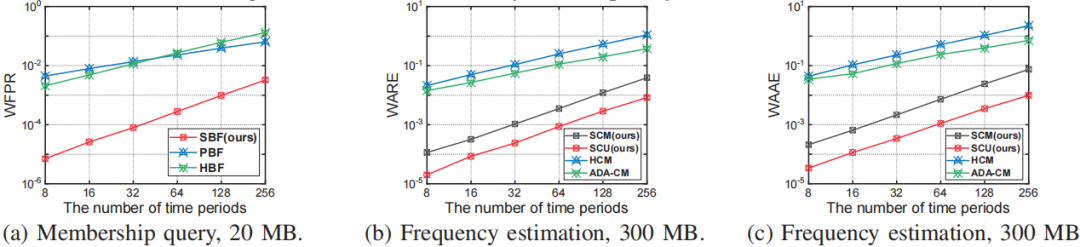
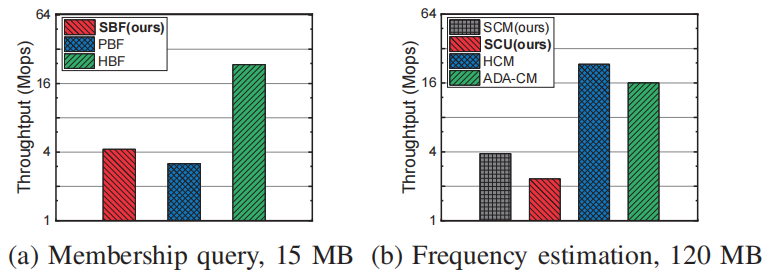
为了满足上述要求,论文提供了一种新的数据流处理结构,称为Stair Sketch。它包含了许多原子sketch,在一个时间段内,sketch数量越多,查询的准确率就越高。其关键思想是将原子sketch组织成楼梯的形状,每个时期使用的原子sketch的数量就如楼梯的高度一样增加。如图1所示,时间段1,2,3,4已经过去,它们所拥有的的原子sketch数量分别为1,2,3,4。在第5个时间段来临时,为其分配4个原子sketch,并分别从前4个时间段内删除一个sketch,被删除的sketch可以放在磁盘等地方。这样保证了内存的消耗量是固定的。图1拥有10个原子sketch的Stair SketchSketch:sketch通常基于hash,使用如图 2所示的数据结构,由d个hash函数(图中为3)以及一个数组组成。当插入新数据时,通过d个独立的hash函数对其进行映射后插入数组中对应的d个位置。Sketch通过数组中存储的信息对查询进行估计。以布隆过滤器为例,数组的每一项是一个bit,初始时全置为0。当插入新数据时,通过d个hash函数将数组中的d个位置置1。在查询一个数据是否出现在数据流中时,布隆过滤器通过检查映射后的d个位置是否均为1来判断数据是否存在,全为1则存在,否则不存在。显然,由于hash碰撞,布隆过滤器存在假阳性问题,即不存在数据的数据可能判断为存在,但假阳性率(FPR)相当小。数据流S:S={ <e1,t1>,<e2,t2>…,<en,tn>…}。其中ei属于集合U={1,2,…N},ti是一个单调递增的时间戳,指示ei在什么时候出现过。Stair Sketch是一个通用结构,可以应用于许多现有的sketch,例如布隆过滤器。下面以布隆过滤器为例进行介绍。图 3是Stair Sketch的基础版本,其中每一个方格是一个布隆过滤器,方格中的数字是它所处的时间戳。假设需要在内存中维护最近m个时间段的信息,Stair Sketch会包含m*(m+1)/2个布隆过滤器,每个布隆过滤器占相同的大小w,占用的总内存大小就是m*(m+1)*w/2。给定内存限制,通过调整w和m可以很容易满足需求。如图 3所示,Stair Sketch是动态地进行建立和更新的。在第一个阶段,还未超过内存上限时,在第k个时间段,建立k个布隆过滤器(k<=m,图中m=4),每个布隆过滤器使用d个独立的hash函数。对于每个在第k个时间段插入的数据,对其中的k个布隆过滤器均执行一次插入操作。图中右上角就是一次具体的插入流程,4个布隆过滤器的对应位置被置1。在布隆过滤器达到内存上限时,进入第二阶段。在这个阶段,当第k个时间段开始时(k>m),对于前m个时间段,均删除其中一个布隆过滤器,利用释放的内存为当前时间段新建m个布隆过滤器。如图 3左下角,进入第5个时间段时,第1、2、3、4个时间段最上面的一个布隆过滤器均被删除,然后第5个时间段新建了4个布隆过滤器。在查询数据是否出现在第k个时间段内时,对于该时间段内的每个布隆过滤器进行一次查询,当且仅当所有布隆过滤器返回true时可以说明该对象可能出现在该时间段内。可以证明,Stair Sketch的基础版本已经满足了之前提到的时间渐进性,但它依旧存在两个不足,优化版本将分别对这两个不足进行改进。垂直采样:给定固定的内存大小M,参数m和w需要满足m*(m+1)*w/2<=M。如果想要记录更长的历史,即增加m,那么所需的布隆过滤器数量将呈平方级别增长,在内存大小不变的情况下,就需要大量减小w,带来更高的假阳率。论文因此提出了垂直采样技术,在图 3中,同一条水平线上的一组布隆过滤器称为一个layer,图中有4个layer,从上到下分别有1、2、3、4个布隆过滤器。论文发现,为了保证相对准确的信息,并满足时间渐进性的要求,只需要保存那些层数为2的幂的layer就够了,如图 4所示,当m=8时,只保存层数为1、2、4、8的layer。经过垂直采样后增加m所需要增加的布隆过滤器数量与m成线性关系,因此可以更准确地记录更长的历史。水平共享:对于一个特定的布隆过滤器,将插入其中的数据量称为它的负载。由于数据流具有突变性,这将导致严重的负载不均衡问题。在一些时间段布隆过滤器可能只有很小的插入量,然而在基础版本中仍然会为其创建m个布隆过滤器,这会导致空间的浪费。虽然数据流具有突变性,但根据大数定理,多个时间段内的数据量相对于一个时间段内的数据量会稳定许多,因此优化版本使用共享机制来解决负载不均衡的问题。它将多个布隆过滤器组合成一个更大的布隆过滤器,并用它记录多个时间段。如图 4所示,第4层的1,2,3,4时间段共享一个布隆过滤器,第3层的5,6时间段共享一个布隆过滤器。在这个大的布隆过滤器中,优化版本使用[1]中提出的移位技术以区分不同时间段内的对象。简单来说,移位技术是以k为偏移值,与原来的hash值进行相加后作为插入布隆过滤器的位置。假设数据为e,在第k个时间段内插入,hash值为h(e),布隆过滤器长度为w,则将其插入布隆过滤器的第(h(e)+k)%w位。在优化后,Stair Sketch第1层有1个布隆过滤器,其它层均只有2个布隆过滤器。查询操作与插入操作与基础版本类似,只是需要寻找应该作用于哪个布隆过滤器。数据集:论文一共使用了3个数据集进行评估,其中CAIDA[2]和Web page[3]数据集为真实数据集,CAIDA数据集包括1.6*106个不同的数据,总的数据量为4.2*108,Web Page数据集包括1*106个不同的数据,总的数据量为3.2*107。合成数据集遵从Zipf分布,包括952888个不同的数据,总的数据量为3.2*107。Web Page数据集与合成数据集的到达时间是通过均匀分布生成的。评价指标:论文主要包含3个评价指标,1) FPR,假阳率;2) AAE,平均绝对误差;3) ARE,平均相对误差,这些指标都是越小越好。为了评估时间渐进性,论文还提出了加权的FPR:WFPR。对比方法:由于Stair Sketch可以同时用于隶属度查询(查询一个数据是否出现在数据流钟)和频次估计(查询一个数据出现在数据流钟的次数),而其它的最先进技术均只能完成其中一个功能,因此,论文分别寻找了用于隶属度查询和频次估计的最新技术来进行比较。在处理完整个数据流后,分别测试各种方法的FPR,如图 5所示,随着时间的增长,HBF和SBF(论文的方法)的FPR均出现了下降的趋势,因此它们满足时间渐进性,而FPR并不具备这个性质。同时,SBF的FPR一直保持在最低的水平。为了验证错误渐进性,论文提出了新的评价指标WFPR,它将多个时间段内的FPR进行加权和,并给最新的时间段赋予更高的权重。论文接下来测试了在内存和时间段数发生变化后各类方法的表现。从图 6中可以看出,在不同的内存大小下,SBF均达到了最低的SFPR,大多数情况下,SBF的错误率比其它方法低两个数量级。从图 7中可以看出,随着时间的增长,各类方法的估计误差均有所增长。这是因为随着时间的增长,数据结构中记录的数据量以及粒度也随之变大。在内存预算不变的情况下,插入量越大准确度往往越低。Stair Sketch的WFPR往往比其它方法的低9.5倍。如图 8所示,SBF的吞吐量表现往往优于PBF,然而却差于HBF。这是因为SBF和PBF更专注于减少范围查询的延迟。在记录L个时间段时,PBF和SBF的插入时间复杂度和范围查询复杂度均为O(log(L)),而其它方法的插入时间复杂度为O(1),但其范围查询的时间复杂度为O(L)。本文介绍了Stair Sketch,一个用于数据流查询的估计型数据结构。由于人们往往对最新的事物感兴趣,Stair Sketch为新的数据提供了更高的查询精确度。Stair Sketch的关键思路在于将基础的Sketch组织成楼梯的形状,这样保证了时间渐进性。同时,Stair Sketch是一个通用的框架,可以应用在多种Sketch上。实验证明了Stair Sketch在比其它先进方法的准确率高5倍以上的同时也保证了时间效率。[1]Tong Yang,
Alex X Liu, Muhammad Shahzad, Yuankun Zhong, Qiaobin Fu, Zi Li, Gaogang Xie,
and Xiaoming Li. A shifting bloom filter framework for set queries. Proceedings
of the VLDB Endowment, 9(5), 2016.
[2] The CAIDA Anonymized Internet
Traces. http://www.caida.org/data/overview/.
[3] Real-life transactional
dataset. http://fimi.ua.ac.be/data/.
| 重庆大学计算机科学与技术专业在读硕士一年级学生,重庆大学START团队成员,主要研究方向:时空数据管理 | 
|
时空艺术团队(START,Spatio-Temporal Art)来自重庆大学时空实验室,旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!