时间序列数据通常有规律的时间间隔，在生活中会产生大量的时间序列数据，例如GPS信号，户外的空气质量数据。但是由于传输延迟，设备故障，重复请求等情况会导致这些时间序列数据很“脏”，影响后续的分析处理。本篇文章将带来国际顶级数据库会议VLDB 2022上的论文：《On Repairing Timestamps for Regular Interval Time Series》，文章主要针对这些“脏”的时间序列数据进行合理的修复。
一、问题背景
对于时间序列数据，例如物联网场景中定期收集的传感器数据，户外监测器定期记录的空气质量数据，从卫星上收集的GPS信号数据。这些设备通常以实现预定的频率收集数据，这种规则间隔时间序列反映了数据的变化趋势，而且更加容易进行分析和存储。但是由于下列问题导致时间戳不够精确，导致时间序列时间间隔不规则。
1. 传输延迟，一般物联网数的时间戳在终端接受到数据后进行加盖，但是由于网络不稳定，导致接收到数据时加盖的时间戳不规则。如图1(a)所示。
2. 数据缺失，由于传输错误或设备故障，如传感器损坏，数据可能丢失，如图1(b)
3. 重复请求，例如自动重复请求（ARQ）这样的数据传输机制可以通过不可靠的通信信道重复发送数据包，以实现可靠的数据传输，但是也会造成数据的重复传输导致出现冗余，如图1(c)。
图一是一个真实场景的情况，展示了车辆场景中(a)、(c)和(e)中的不规则间隔时间序列的三个例子，以及它们在(b)、(d)和(f)中的相应修复。图1(g)为引擎速度的连续数据的时间间隔。大多数都在60秒左右。但是，由于数据噪声极大，图1(h)中汽车速度数据的间隔很难确定。
处理不规则的时间间隔可以进行快速傅里叶变换（FFT）分析，并很好地改善存储空间。例如为了检测异常发动机行为，采用FFT的频域分析技术需要规则的间隔时间序列。此外，为了有效地存储时间序列数据，经常采用类delta编码和压缩技术，规则的时间序列可以更好地进行数据的压缩。
文章主要针对不规则的时间序列数据的延迟点、缺失点和重复点。移动一个延迟的点只更改时间戳而不更改其值，删除一个重复的点也不需要处理该值。但是，对于插入一个缺失的点，应该同时修复它的时间戳和值，本文只专注于插入缺失的时间戳，而不进行缺失值的推断。
有以下几个问题导致修复时间戳存在一些挑战，如何找到最小修复成本？如何找到时间序列开始时间？如何找到时间序列长度？对于图1(h)这种情况如何确定时间间隔？
本文将规则间隔时间序列的时间戳修复问题形式化，最小化移动、插入和删除操作的成本。设计了一种基于动态规划的精确方法，寻找具有最小距离代价的不规则区间时间序列与规则区间时间序列的匹配，并确定规则区间时间序列的长度。并设计了一种基于双向动态规划的近似算法，显著降低了时间成本。文章对各种现有的方法进行了全面的评估，在修复的时间戳和下游任务中，例如，频域分析和数据压缩。
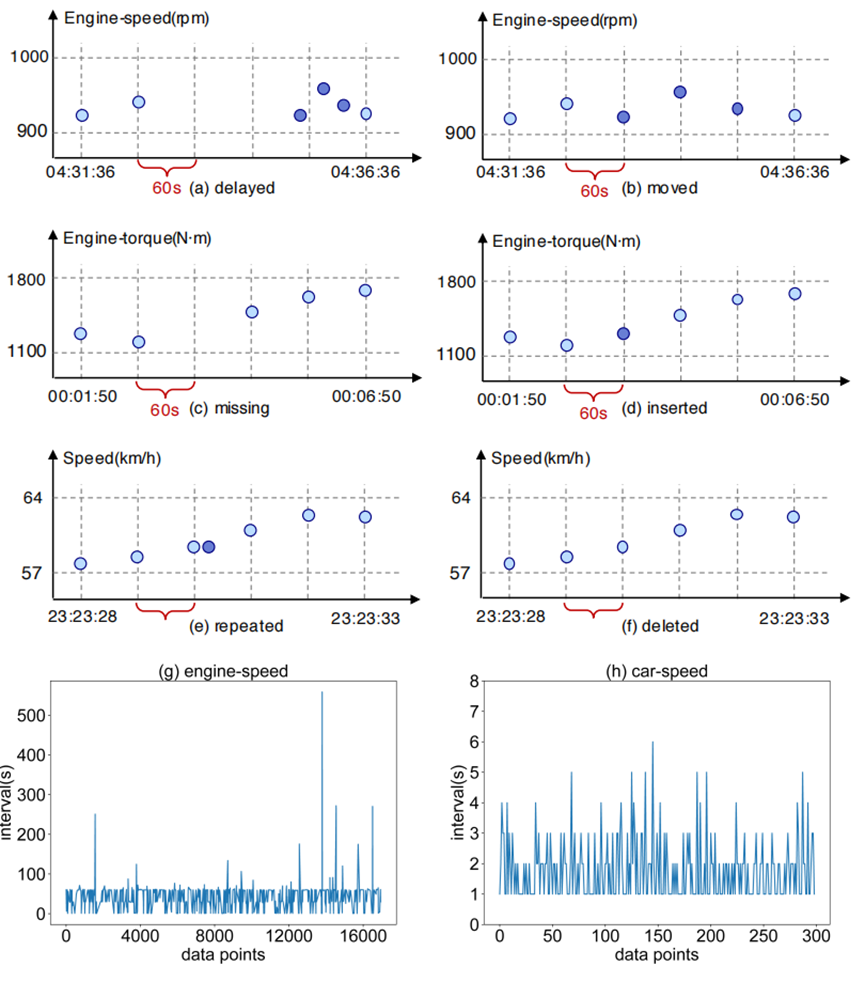
图1时间序列不规则的情况
二、问题定义
时间序列修复的目标是以最小的代价获得一个修复好的规则的时间序列数据，并且给出修复后和原数据的匹配。对于找到最小修复代价所产生的子问题的处理顺序如图2所示，给定一个输入时间序列t，为了将其修复为一个规则的间隔时间序列s，首先计算s的区间𝜖𝑇。接下来确定其起始点𝑠0。然后，根据时间间隔和起始点找到s的最佳长度𝑚。最后，从t到s找到匹配𝑀。
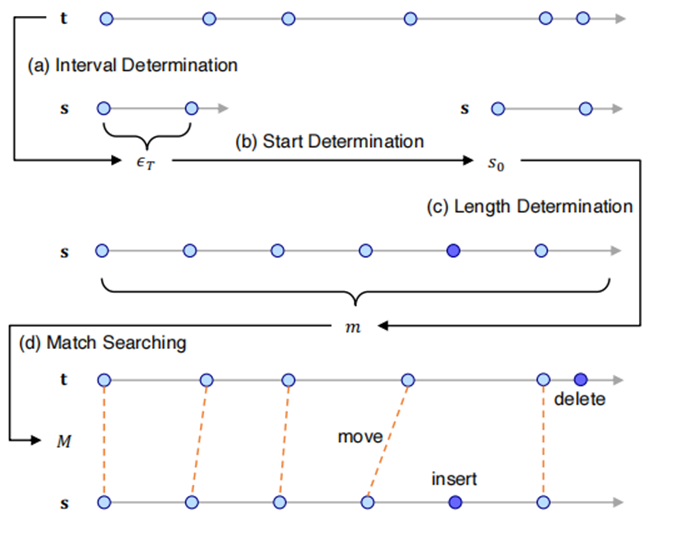
图2修复的参数确定顺序
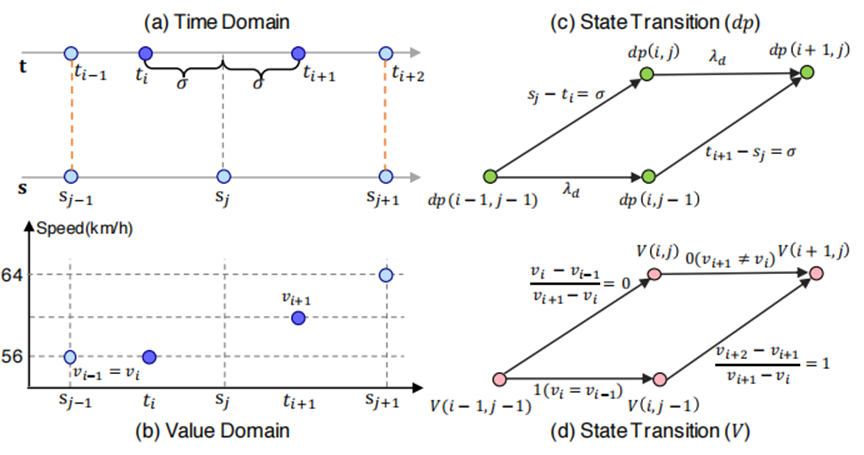
图3使用值来决定匹配的示例
三、精确算法
1.匹配搜索
本文针对匹配和修复代价，设计了一种基于动态规划的匹配搜索问题的多项式时间算法。状态转移方程如下：
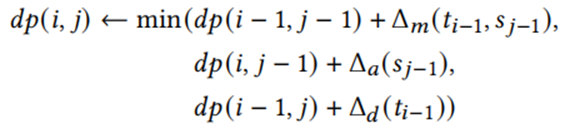
其中dp(i,j)为最小修复成本，Δm为移动成本，Δa为插入成本，Δd为删除成本。算法1给出了找到最小成本的序列的过程。算法2给出了找到最佳匹配的过程。
但是仅使用动态规划会导致得到多个不同的匹配项，所以引入数据值的特征来做出进一步的决策。图3(a)是需要进一步决策的操作的示例，这种情况下删除任何一个ti的修复成本的都是相同的。但是在图3(b)中𝑣𝑖−1 = 𝑣I 代表着可能是重复点。所以为了更好的判断，文章加入了一个状态转移矩阵，随着dp的更新一起更新，这样来更好的进行决策。
对于延迟的数据，需要选择值的波动𝛿𝑣𝑖 = |𝑣𝑖 − 𝑣𝑖−1 |更加接近的情况，即ti前后的值波动𝛿𝑣𝑖 和𝛿𝑣𝑖+1更加近似，因此按照如下公式进行更新V(i,j)：
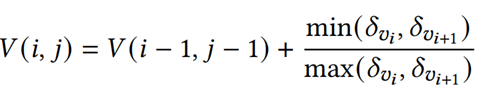
对于重复的数据，数据值与前一个点相同，所以按照如下公式进行V的更新
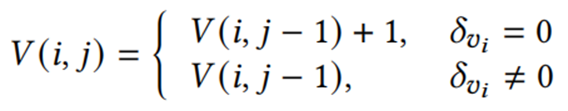
对于丢失的数据，丢失值的相邻两个数据之差会突然较大，所以我们可以根据相邻值的差值与平均差值进行比较。
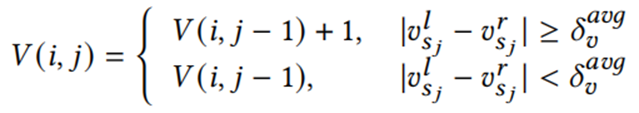
其中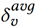
是平均的时间序列中两点的差值。
图3(c)和图3(d)所示。对于有相同修复成本的数据𝑉 (𝑖, 𝑗) + 0 = 𝑉 (𝑖 − 1, 𝑗 − 1) + 0 < 𝑉 (𝑖, 𝑗 − 1) + 1 = 𝑉 (𝑖 − 1, 𝑗 − 1) + 2。所以选择删除ti然后将ti+1移动到sj
2.确定其他参数
对于时间序列的长度，文章给出了其上界，在算法1第15行里，随着动态规划的过程动态选择在上界内的时间序列长度。
对于起始时间的确定，文章给出了一个起始时间的简单的边界，并且和成本结合在一起可以进一步限制。
对于时间区间的确定。文章提出了基于成本的时间间隔边界。引入了最小匹配的两个性质来导出成本边界，文章给出了相关证明，1）插入和删除操作不能同时在相邻的移动中出现，2）插入操作不能出现在序列的开始或结束。为了有效地找到𝜖𝑇，文章从𝜖𝑚𝑑即有可能出现的时间间隔的中值开始遍历，并逐渐增加或减少它，不超过给定的界限。
对于这些参数的边界，根据算法3进行修剪。
其中需要确定𝜆𝑎和𝜆d，由于处理缺失或重复的点将改变数据点的数量，所以直觉是设置𝜆𝑎=𝜆𝑑=𝜆。但是如果𝜆过小，会导致过度检测缺失和重复点，因为插入成本低于数据的移动，如果𝜆过大，会使插入和删除变得困难。文章建议在实践中使用𝜆𝑎=𝜆𝑑=𝜆=𝜖𝑚𝑎𝑥。
四、近似算法
由于中值在处理有噪声的时间序列数据时的稳定性，我们在试图保持精度的同时，做了两个近似值来提高效率。
我们提出中位数近似的方法，直接将原始时间序列t的中位数时间戳作为目标s的中位数时间戳，受到中位数的稳定性启发。如下所示，使用这个中值近似，我们不再需要遍历s的所有可能。
首先，定义中位数，设置中值点，我们将问题的重点发在双向动态规划算法的状态转移方程上。我们将算法1中提出的动态规划算法修改为双向动态规划的中值逼近。设𝑑𝑝𝐿(𝑖,𝑗)表示从时间序列t𝐿[𝑖]到s𝐿[𝑗]的最小修复成本，而𝑑𝑝𝑅(𝑖,𝑗)表示从时间序列t𝑅[𝑖]到s𝑅[𝑗]的最小修复成本，我们有下面的状态转移方程：
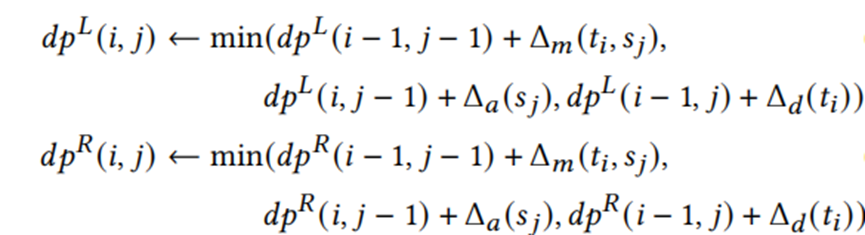
整体的状态转移方程是两个在两个方向上的状态的组合：
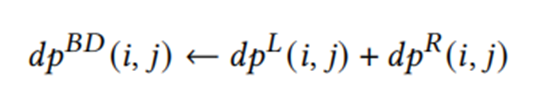
实际上，双向动态规划算法的状态转移方程是为了双向进行动态规划算法。具体见
算法4.
确定近似区间。观地看，如图1(g)所示，原始时间序列t中的大部分时间间隔都接近于
，即约60s。因此，文章建议通过区间的中位数来计算
的近似间隔，即:
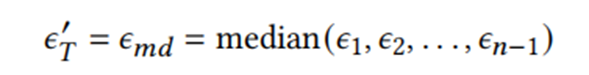
五、实验
1. 实验设置
表1 数据集的特性。Dataquality issues是指存在于原始数据集中的数据质量问题。Truth表示我们拥有的数据集的真实参数。
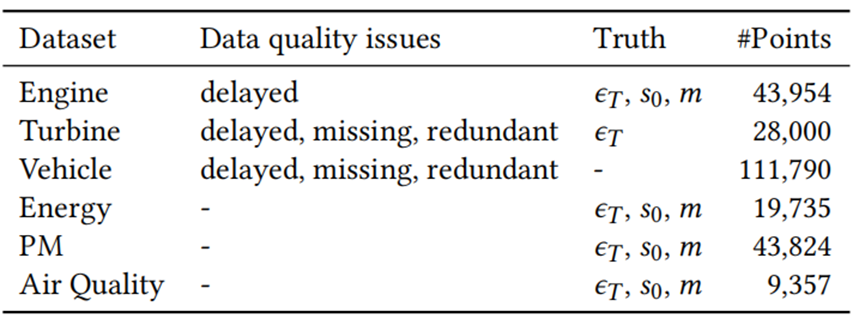
本实验采用的数据集如表1所示。前三个数据集来自文章的合作伙伴公司，其中的引擎数据集有真实时间戳，而涡轮机数据已知每7秒收集一次，但起始和长度未知。对于具有规则间隔时间戳的数据集，包括能量、PM和空气质量，我们首先基于高斯分布向时间戳中注入随机延迟。然后引入缺失点和冗余点，由1%的错误率控制，即将1%的重复数据注入到数据中，并选择1%的缺失点进行删除。
与现有方法比较，对于每个数据集，文章将与现有的方法在在时间序列之间的RMSE损失RMSEt、在值之间的RMSE损失RMSEf和时间成本上进行了比较。
2. 修复实验对比
如表2所示，由于它精确地搜索修改的最低成本，RIR-Exact在所有数据集上，在RMSEt和RMSEf方面都优于其他方法。出于同样的原因，RIR-Appr在这两个指标上也显示出了稳定的竞争结果，但时间成本比RIR-Exact更低。由于SCREEN是基于滑动窗口进行的，它不能针对整体进行修复，因此显示出比其他方法更差的RMSE结果和更低的时间成本。CTTC使用时间约束来修复时间戳，由于它没有考虑到点的插入和删除。在大多数数据集中，它的性能比RIR-Appr要差。
表2：RIR-Exact和RIR-Appr与现有方法相比的𝑅𝑀𝑆𝐸𝑓、𝑅𝑀𝑆𝐸𝑡和时间成本
3. 时间序列修复应用分析
图4展示了在能量数据集上使用频域分析方法修复的时间序列的时间成本。对于间隔不规则的原始数据，只能应用NUFFT，因此显示的时间成本最大。此外，图4进一步显示了RMSE的结果。我们的RIR-Exact显示了最佳的性能，RIR-Appr在RMSE中明显优于其他基线方法，再次验证了我们的近似修复的优越性:
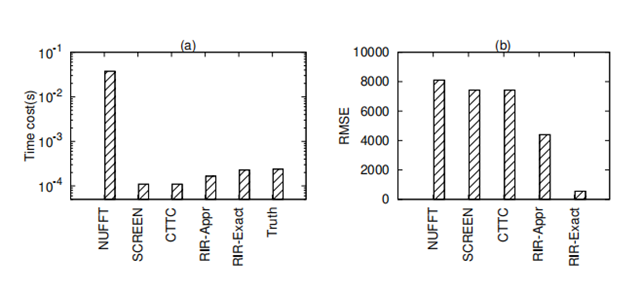
在压缩处理实验中，文章使用时间序列数据库存储0.6万-300万个数据点的原始和修复的时间序列数据。对于每个尺寸，文章将数据插入到数据库中，并记录存储空间的增加。图5显示了存储空间的结果和间距时间比。由于deltaof delta原理，规则的间隔时间序列（时间戳上的delta of delta为0）占用最小的存储空间。如图5(b)所示，Space Saving Ratio稳定地保持在15%左右，也就是说，规则的间隔时间戳被有效地压缩。
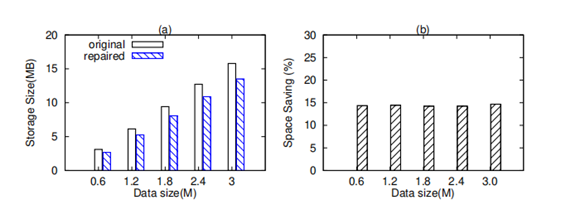
图5 在数据压缩上的应用程序
4. 对参数λ确定的评价
在实验中，文章将成本λa和λd设置为ϵmax。为了验证设置λ=ϵmax的有效性，文章进一步通过改变不同的λ进行了实验。如图6所示，反映了各种λ条件下的RMSEf和时间成本：
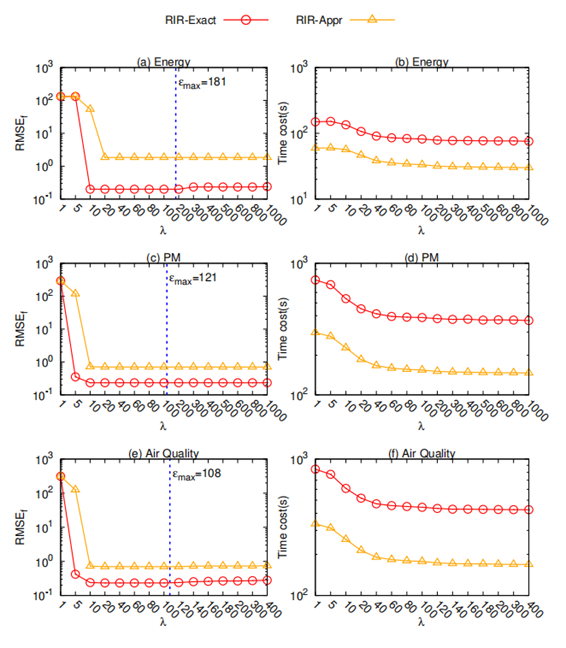
总的来说，RIR-Exact和RIR-Appr是稳定的，当λ足够大时，它们对λ不太敏感。在能源和空气质量方面，当λ>ϵmax时，由于一个更大的λ可能会使删除和插入变得困难，RIR-Exact或RIR-Appr的RMSEf开始有所增加。从图6还可以看出，由于一个更大的λ可能会引入更少的删除和插入，从而减少匹配M的长度，使得时间成本会随着λ的增长而减少。根据评估，λ=ϵmax可以平衡准确性和时间成本。
六、总结
在本文中，为了修复规则时间序列中的“脏”时间戳，文章采用了移动、插入和删除数据点。修复问题有多个相互作用的因素需要确定，包括时间序列的起始时间、长度和时间间隔，如果没有提前给出，则使其具有挑战性。此外，还设计了一种基于双向动态规划的近似方法，以本文实现更有效的修复工作。实验证明了文章的方法在修复精度以及类似于频域分析和数据压缩等下游应用方面的优势。
|
