
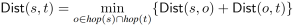 。通过这种方法求解最短路径距离的时间开销为O(|L(s)|+|L(t)|)。
。通过这种方法求解最短路径距离的时间开销为O(|L(s)|+|L(t)|)。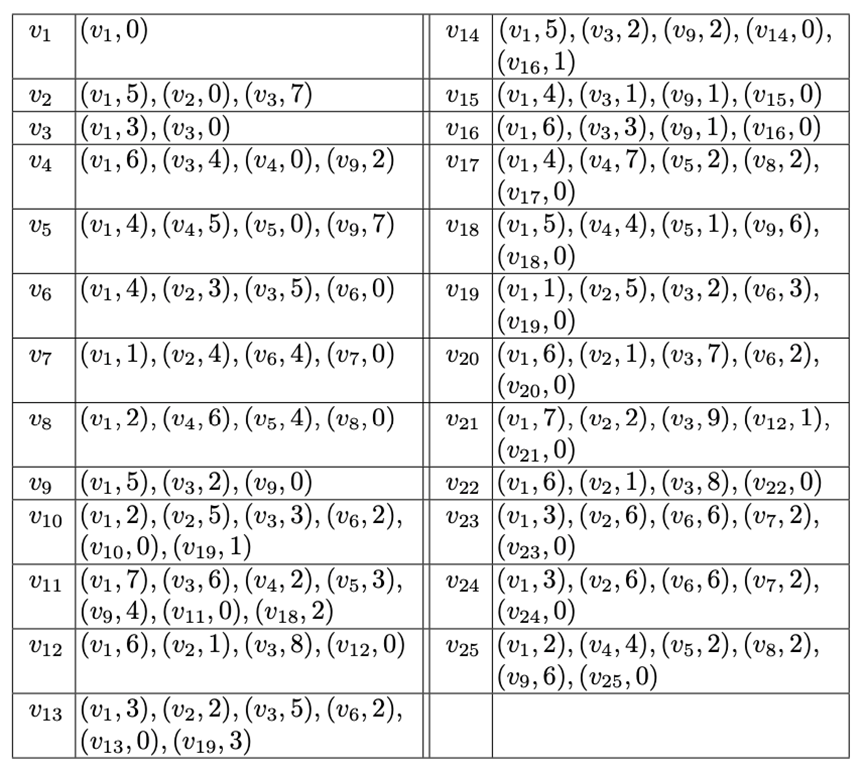
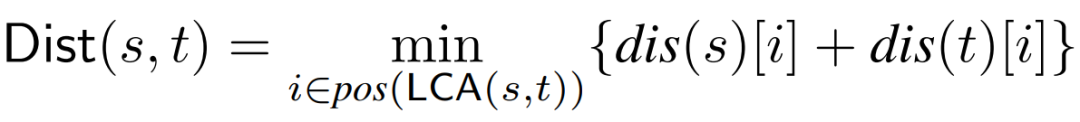 。
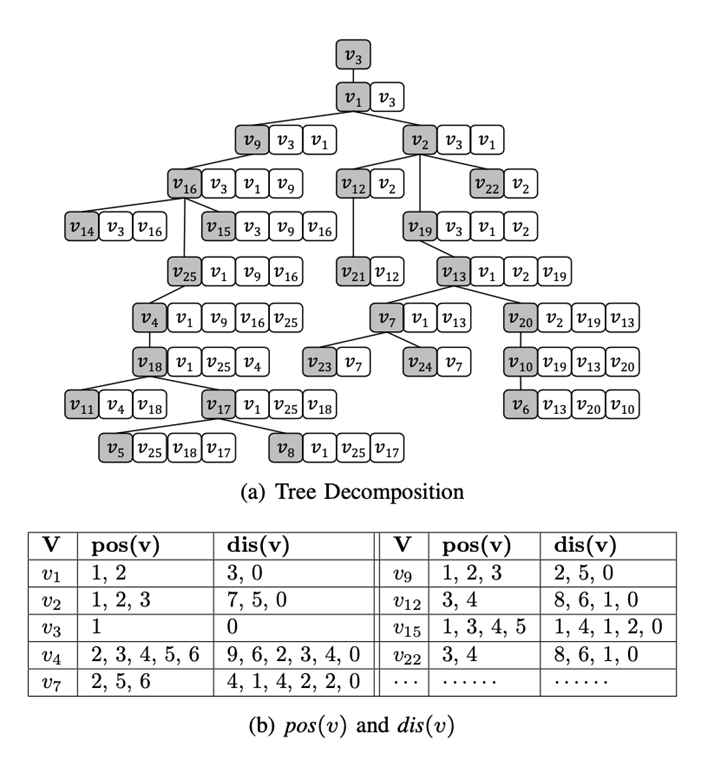
。
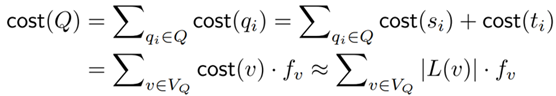


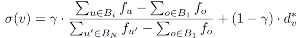 ,其中dv*=dv / dmax,γ是平衡参数,Bi是vi所属的区块。此处提到的区块是由论文提出的区块分区技术生成的,之所以引入区块分区技术,是因为如果像σ(v) = γ⋅fv* + (1 - γ)⋅dv*这样直接地引入频率参数,将会导致生成的树分解高度和宽度都比原MinDegree方法生成的大,从而造成额外空间开销。引入区块分区技术之后,所有顶点被分成N = ⌈n/η⌉个区块,每个区块的最大大小为η,然后区块按照由度数和查询频率决定的顺序处理,对于一个区块内的顶点,则按照顶点度数的顺序处理。
,其中dv*=dv / dmax,γ是平衡参数,Bi是vi所属的区块。此处提到的区块是由论文提出的区块分区技术生成的,之所以引入区块分区技术,是因为如果像σ(v) = γ⋅fv* + (1 - γ)⋅dv*这样直接地引入频率参数,将会导致生成的树分解高度和宽度都比原MinDegree方法生成的大,从而造成额外空间开销。引入区块分区技术之后,所有顶点被分成N = ⌈n/η⌉个区块,每个区块的最大大小为η,然后区块按照由度数和查询频率决定的顺序处理,对于一个区块内的顶点,则按照顶点度数的顺序处理。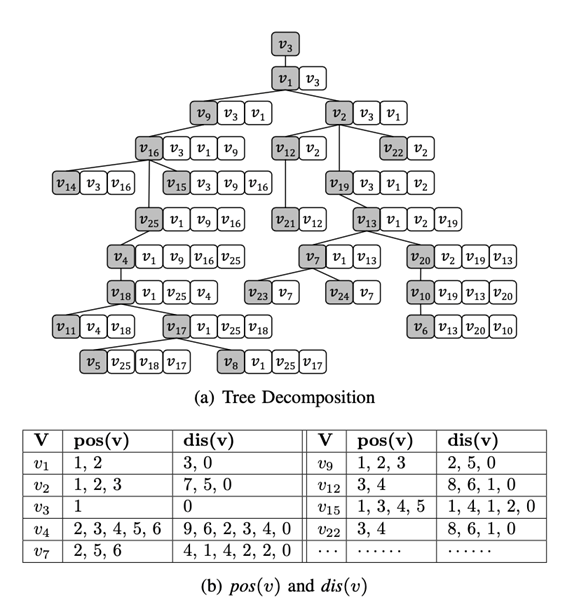

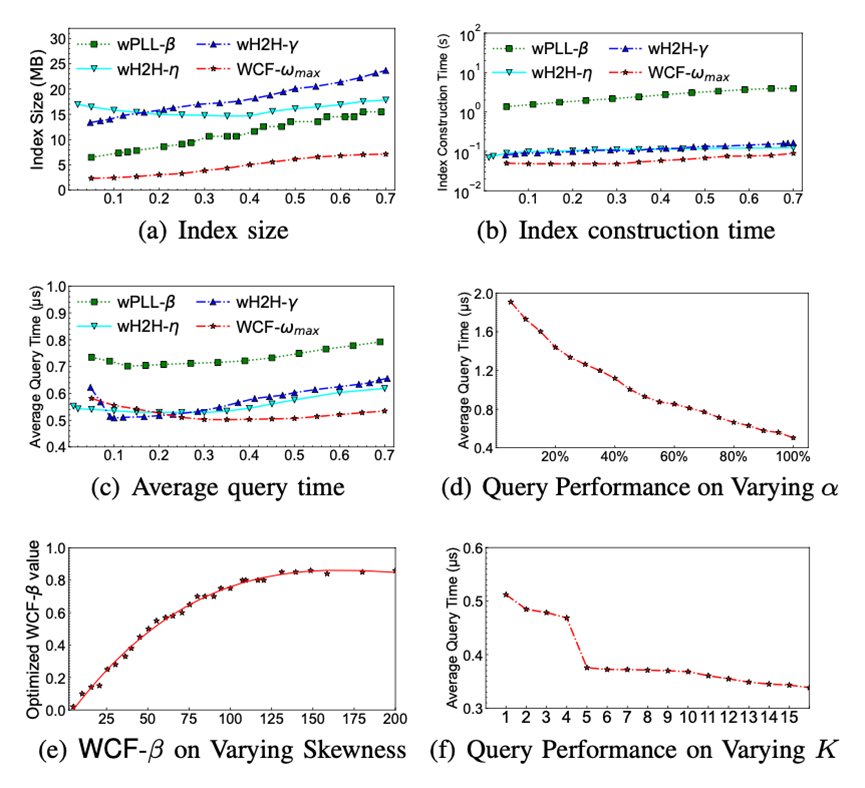
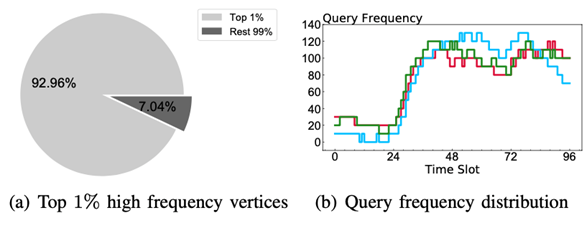
 值的增加而急剧降低,但是在K=5之后降低非常缓慢,所以论文默认设定K为5。
值的增加而急剧降低,但是在K=5之后降低非常缓慢,所以论文默认设定K为5。
本文作者 陈泽超 |  |
文章转载自时空实验室,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






