通过研究发现交通预测时各区域间具有动态、周期性和联合时空依赖性的问题。现有技术通常以解耦的方式分别考虑空间和时间依赖关系,或者在使用大量需要调整的超参数进行训练时,计算开销非常大。本次为大家带来数据挖掘顶级期刊TKDE上近期收录的论文:《A Lightweight and Accurate Spatial-Temporal Transformer for Traffic Forecasting》,该文提出了一种新颖的、轻量级的、精确的、具有信息融合和区域采样功能的交通预测时空转换器。

交通预测是预测一个城市下一个时间段的流入(即单位时间到达对象的数量)和流出(即单位时间离开对象的数量)。对象可以是人、车辆、货物/物品等。交通预测在交通、零售、公共安全、城市规划等领域都有重要的应用。虽然有很多集中在深度学习提高预测精度的预测模型,但是性能的提升却伴随着参数的增加和训练资源的增加,这就导致训练和部署大型深度学习模型的成本高昂,因此,一个轻量级且高效的模型对于快速交付和部署至关重要。此外,区域交通在空间上和时间上是相关的,这种依赖在不同的时间隙上是动态的,它可能具有时间周期模式。因此,为了准确预测区域交通,无论区域之间有多远,考虑区域之间的动态性和联合的时空(ST)依赖性是至关重要的。鉴于此,本文提出了一种新颖的、轻量级的、精确的、具有信息融合和区域采样功能的交通预测时空转换器ST-TIS。ST-TIS基于考虑区域之间的时空依赖关系,尤其是考虑了具有信息融合模块(IFM)的任意单个时间片的动态时空依赖性,以及使用注意力机制的多个时间片之间的时空依赖性可能周期性特征,提出了数据驱动的转换器方案。此外,本文提出了一种新的考虑到计算效率的区域采样策略,利用转换器框架来学习区域依赖关系,与此同时还采用了一种新的区域采样策略来生成连通区域图,并基于该图学习其依赖性。在ST-TIS中,通过信息传播保证考虑到任意一对区域之间的依赖关系(近距离和远处依赖关系),计算复杂度从 降低到
降低到 ,其中,n是区域的数量。
,其中,n是区域的数量。

 来表示一个区域ri,其中只有Si中的第i个元素为1,否则为0。然后,我们对一个区域ri的位置信息进行编码如下:
来表示一个区域ri,其中只有Si中的第i个元素为1,否则为0。然后,我们对一个区域ri的位置信息进行编码如下: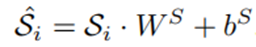
 嵌入的一个热向量来表示第i个时间槽。在那之后,我们通过以下公式来学习时间:
嵌入的一个热向量来表示第i个时间槽。在那之后,我们通过以下公式来学习时间: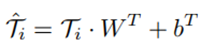
 前时隙中的流量:
前时隙中的流量:
 与步长为1和f的输出通道的一维卷积应用于其流入和流出周围的观测值,以提取不同的模式。ri在tj处的流嵌入
与步长为1和f的输出通道的一维卷积应用于其流入和流出周围的观测值,以提取不同的模式。ri在tj处的流嵌入 计算为:
计算为: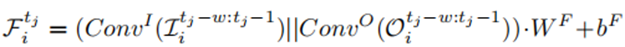
 时间隙,其中
时间隙,其中 是一个匹配函数,融合过程被定义为:
是一个匹配函数,融合过程被定义为: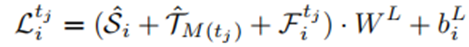
 。因为给定n个节点,当β = 2时,我们应该有
。因为给定n个节点,当β = 2时,我们应该有 ,并且构造图的最小度k为
,并且构造图的最小度k为 。这样,对于目标区域,我们只需要将
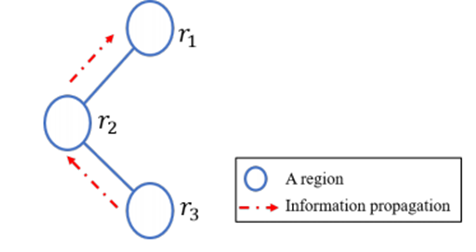
。这样,对于目标区域,我们只需要将 区域的嵌入聚集到聚集层中,就可以通过信息传播在双层聚集过程中捕获来自其他区域的影响。这样的设计,我们不需要计算任何对区域之间的注意力分数和聚合的嵌入所有n个区域的目标区域,从而将每一层的计算复杂度降低到
区域的嵌入聚集到聚集层中,就可以通过信息传播在双层聚集过程中捕获来自其他区域的影响。这样的设计,我们不需要计算任何对区域之间的注意力分数和聚合的嵌入所有n个区域的目标区域,从而将每一层的计算复杂度降低到 ,并解决了长尾问题。
,并解决了长尾问题。 来表示相似度矩阵,其中
来表示相似度矩阵,其中 是ri和rj之间的相似度。基于
是ri和rj之间的相似度。基于 ,连通图的生成过程如图3所示:
,连通图的生成过程如图3所示: 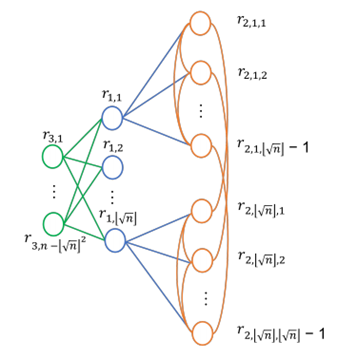
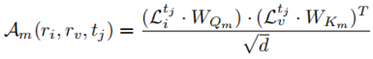
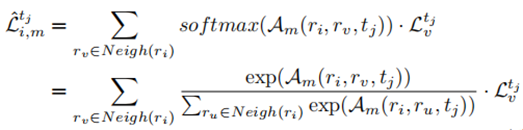
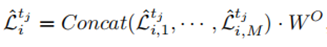
 的输出传递到一个完全连接的神经网络,如图4所示。我们还在这两层之间使用了残差连接。由于信息的传播是通过一个多层的网络结构来实现的,因此,我们堆叠各层的α时间。我们将DLI的最终输出表示为
的输出传递到一个完全连接的神经网络,如图4所示。我们还在这两层之间使用了残差连接。由于信息的传播是通过一个多层的网络结构来实现的,因此,我们堆叠各层的α时间。我们将DLI的最终输出表示为 ,其中
,其中 是区域ri在tj处的嵌入。
是区域ri在tj处的嵌入。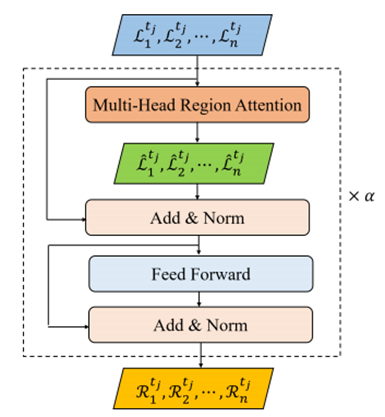
 与其他历史时隙
与其他历史时隙 (其中
(其中 )的依赖性之间的相关性来学习周期依赖性。然后,根据嵌入的相关性在不同的时间段进行聚合,为ri生成新的ri嵌入。
)的依赖性之间的相关性来学习周期依赖性。然后,根据嵌入的相关性在不同的时间段进行聚合,为ri生成新的ri嵌入。 的第z个依赖性计算如下:
的第z个依赖性计算如下: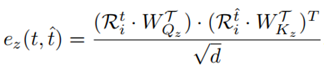
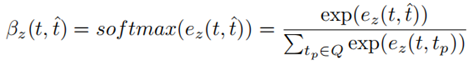
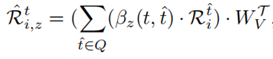
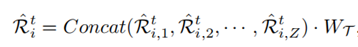
 ,其中
,其中 是用于学习的历史时隙的数量。
是用于学习的历史时隙的数量。 ,预测网络使用全连通网络预测流入和流出。预测函数的定义为:
,预测网络使用全连通网络预测流入和流出。预测函数的定义为: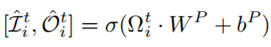
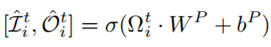
 作为评估度量。
作为评估度量。
 |







