定位技术的发展使得定位服务在社交网络中起到越来越大的作用,在线社交网站如推特和四方都允许用户对他们的社交帖子进行地理标记。这产生了新的数据分析问题,如检测流行的主题趋势。而本篇文章带来的国际顶级的数据库期刊VLDBJ 2022上的论文:《Reverse spatial top-k keyword queries》[1]研究了相反的问题。

1.背景
在先前的工作中,为解决上面提出的流行趋势检测等问题,常在时空领域使用各类top-k算法,即给定一个查询区域,找到其中出现次数最频繁的k个词语。而本文主要关注它的相反问题:给定一个关键字,找到在哪些空间(或时间)区域内这个关键字是其中出现最频繁的k个关键字之一,称之为RSK查询问题。
这个查询有以下的应用场景:考虑一个广告商,他想要根据推特帖子确定产品在哪些区域内出现过的次数比较频繁,然后可以选取其中较小的区域使用广告牌。另一方面,政治候选人可能会对某个特定的话题在某个区域内是否是受欢迎感兴趣,以确定一个更大场地用于竞选活动。
解决这个问题主要有以下难点:有大量的区域需要进行判断(两个区域不同当且仅当其中包含的数据不同),假如有N个带地理标记的帖子,那么就有N2个不同的空间区域需要判断。
论文提出了一种精确的算法用于解决这个问题,算法首先通过一个过滤步骤来减小搜索空间,之后使用一个基于扫描的细化步骤在修建的空间中寻找答案。论文使用了一个基于网格索引的结构,在网格中添加排序好的关键字列表以避免在查询期间重复处理帖子。为了进一步减小RSK的查询延迟,论文还提出了一个用于估计最优网格单元大小的理论模型。细化过程往往比较慢,因为需要处理大量候选答案,因此,论文还探索了RSK的一个限制版本(RSKR),它只需要返回满足条件的网格,而不是所有满足条件的空间区域。论文提供了近似和精确的算法用于解决RSKR问题。
2.问题定义
令D={o1, o2, … oN}为一个在面积为A的空间矩形内的数据集,D中的每个数据(帖子)o为一个二元组<Loc,Terms>,其中,o.Loc是空间上的一个点,表示为(x, y),用于表示o的地理位置,o.Terms = {t1, t2, … },表示o的关键字集合(无重复项)。令V={∪o∈D o.Terms}表示数据集中所有的关键字组成的集合。给定一个区域R,关键字t在其中的频率fR(t)={count(oi)|t∈oi & oi.Loc∈R},即R中有多少帖子包含该关键字。l-square邻域是一个长为l,边与经纬度平行的正方形区域。当查询关键字q在以空间点p为中心l-square邻域中出现的频率排名位于top-k时,t被称为p的(k, l)频繁项。
论文使用的网格索引记为I,I中的每个单元格存储了位置位于该单元格内的帖子,同时单元格中还存储了一个排序的列表(STL),列表中的每一项包括关键字t即其出现的频率,根据频率进行排序。
RSK查询:给定查询{k, q, l},q是要查询的关键字。返回一组空间区域,其中每一个空间区域需要满足以下条件:对于位于该空间区域内的每一个点p,q是p的(k, l)频繁项。
计算RSK的结果涉及到检查许多区域,因此,RSK的限制版本RSKR只需要返回至少包含一个点p,q是p的(k, l)频繁项的网格。其中,网格是网格索引中使用的网格。
论文首先使用现有的算法对帖子进行筛选,比如根据空间、时间、关键字等进行筛选。在筛选出数据后,使用网格索引对数据进行索引。当改变查询的关键字时,不需要重建索引,但是筛选帖子的条件进行变化时,需要重建索引。系统架构图如图 1所示:
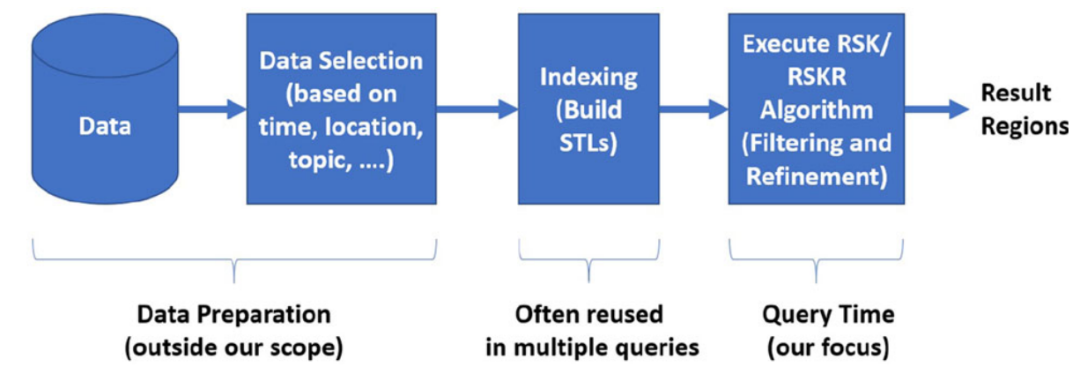
图 1 系统架构图
对于RSK和RSKR问题,论文提出的算法包含以下两个步骤:
1. 过滤步骤:这个步骤的目标是通过找到一定满足条件的网格以及一定不满足条件的网格来修剪搜索空间,其它网格是候选单元格,将在细化步骤进行处理。
2. 细化步骤:在这一步中,对于RSK查询,每个候选单元格将进行平面扫描以得到单元格中满足条件的区域;对于RSKR问题,该步骤以一定的置信度来确定候选单元格是否包含查询关键字q是其(k, l)频繁项的点,如果包含则返回该单元格。
接下来对过滤步骤和细化步骤进行详细介绍。
3.过滤步骤
令lmin为支持的l的最小值,那么,网格的长度c必须满足c <= lmin 2,这是为了能够更好地筛选出一定满足约束的网格以及一定不满足约束的网格。令ηH =⌈l / 2c⌉,ηL =⌊l / 2c⌋。定义网格Ci,j的保守区域CRi,j为满足i-ηL<u<i+ηL且j-ηL<v<j+ηL的网格Cu,v的集合,网格Ci,j的扩展区域Ei,j为满足i-ηH<=u<=i+ηH且j-ηH<=v<=j+ηH的网格Cu,v的集合。如图 2所示,黄色虚线所在的网格的扩展区域与保守区域分别如(a),(b)中灰色网格所示,其中l=3c。
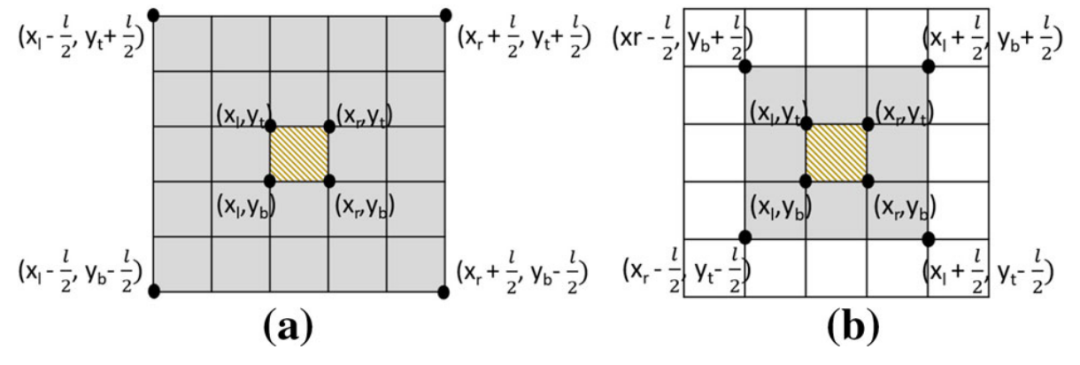
图 2 网格的扩展区域与保守区域
显然,Ci,j中的每个点p的l-square邻域都覆盖了CRi,j,因此,CRi,j中关键字q的出现频率是任意l-square邻域中出现次数的下界。类似的,Ei,j中关键字q的出现频率为上界。因此,如果CRi,j中q的频率大于Ei,j中频率最高的第k项,那么Ci,j一定满足条件;如果Ei,j中q的频率小于CRi,j中频率最高的第k项,那么Ci,j一定不满足条件。
对于剩下的网格,它们可能有部分区域满足条件,接下来的细化步骤将找到这些区域。由于Ci,j中满足条件的l-square邻域都在Ei,j内,因此对Ei,j进行处理即可。
4.细化步骤
论文采用平面扫描算法来找到Ei,j中所有满足条件的l-square邻域。首先固定X轴,对Y轴进行扫描,扫描完后,在X轴上进行移动,重复以上过程,直到无法移动。接下来介绍一些将会用到的术语。
竖条(VS):VS是一个矩形,其中宽在X轴上,长度为l,长在Y轴上,长度与Ei,j相同。如图 3(a)所示,我们把第一个l-square邻域放在Ei,j的左上角,接着向下移动。由于计算l-square中每个关键字的频率非常耗时,论文使用网格索引来加速这一过程。具体步骤为:对于完全被当前l-square邻域覆盖的网格,直接利用其存储的STL来更新关键字的hash表,对于被部分覆盖的网格,找到在被覆盖区域内的帖子后进行更新。
接下来面临的问题是如何找到下一个l-square邻域,由于两个邻域不同当且仅当其中包含的帖子不同,因此,在向下移动时,需要计算与顶部边最近的帖子以及与底部边最近的帖子的距离,其中帖子必须在边的下边,然后根据两者的最小距离来进行移动。然而,有时一次跳过多个帖子并不会影响结果的正确性,因此,论文采用垂直跳跃和水平跳跃来进一步优化这个过程。在垂直跳跃中,可以一次性跳过|fq -fk|个帖子,其中fq为查询关键字q在当前邻域中的频率,fk为当前邻域中排名k的频率。由于一个帖子中没有重复的关键字,这样跳跃不会错过满足条件的邻域。假如当前的邻域是q的一个(k, l)邻域,那么在跳跃过程中,会生成一条线段,如图 3(b)所示,这条线段是跳跃前后的邻域的中心点相连得到的,根据这条线段,在之后的步骤中可以找到在Ci,j中哪些区域满足查询条件。
由于在跳跃前后两个l-square邻域之间有较大的重叠部分,因此还可以利用这部分数据来节省计算关键字频率的时间。即利用上个l-square邻域的关键字频率表,去除只属于上个l-square邻域的部分,再加上仅属于当前l-square邻域的部分。‘
在垂直跳跃到达底边时,接下来将进行水平跳跃。记录VS中每次垂直跳跃的长度,VS可以水平跳跃的长度为其中最小值的1/2。该定理在论文中已得到证明。如图 3(d)所示,VS进行了一次水平跳跃,之后我们将重复上面的垂直跳跃过程。在水平跳跃后,原来保存的线段经过拉伸形成了一个矩形,这个矩形就是满足条件的一个区域。
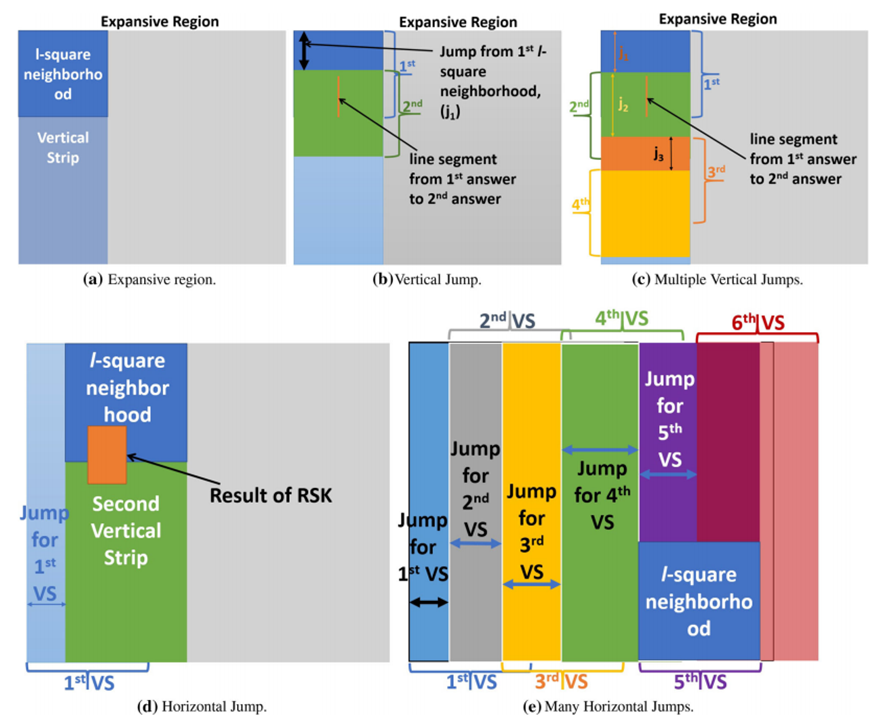
图 3 平面扫描步骤
对于RSKR查询,在细化过程中,只要找到一个满足条件的l-square邻域,就可以直接将当前单元格作为答案返回。但是如果当前单元格不存在这样的邻域,那么细化过程依旧十分耗时。为了减小查询延迟,论文提出了一种划分搜索空间的方案。具体步骤为:对于候选单元格,在其中随机选取一点作为l-square邻域的中心,如果该邻域是q的(k, l)邻域,那么停止搜索。否则根据该点将空间划分成四份。对于划分后的四个子空间,论文依旧在其中各随机选取一点,如果找到答案,那么停止搜索。否则计算四个子空间中q的频率与排名第k的频率的差值,取差值最小的子空间进行第二轮迭代计算。当找到结果或者划分次数到达上限时,算法停止。
5.最佳网格大小估计
论文在本节对RSK和RSKR问题进行了理论分析,以确定最佳的网格大小,进一步降低查询延迟。
令N为数据集中帖子的数量,c为网格的边长,l为l-square邻域的边长,A为覆盖数据集的最小边界矩形(MBR)的面积,假设数据呈均匀分布,那么一个网格内的平均贴子数ρ = N * c2 A。令被一个l-square邻域完全覆盖的网格数为I,被部分覆盖的数量为P。处理一个l-square邻域的花费分为两部分:处理完全被覆盖的网格的花费和处理被部分覆盖的花费。
处理被完全覆盖的网格的花费为I乘以每个被完全覆盖的网格的平均花费。可以证明,至少有(1 / c – 1)2个网格被l-square邻域完全覆盖,论文以这个数字作为I。在进行细化操作时,算法将被完全覆盖的网格的STL进行合并,其中每个STL存储了当前网格的关键字频率。为了计算平均花费,首先需要估计每一个STL的长度,即包含的不同关键字的数量。论文使用Heap定理[2]进行估计:STLsize = K(ρ*y)β,其中ρ = N * c2 / A是每个网格的平均帖子数量,y是每个帖子的平均关键字数量,K和β是自由变量,只和数据集相关。因此,处理完全被覆盖的网格的花费为:T1=I*STLsize=(1/c – 1)2 * K (N * y * c2 / A)β。处理部分被覆盖的网格的花费与之类似,可参考原论文。在算好表达式后,论文利用Wolfram Alpha算法来求最优的c使得花费最小。
6.并行化实现
RSK查询需要准确的答案,是很耗时的。在算法的两个部分中,过滤非常快,因为它只处理STL,而不是实际的帖子。相比之下,细化步骤处理实际的帖子;因此,它需要花费更长的时间(约99%的查询延迟)。在本节中,论文探讨了如何使用并行性来进一步改进细化步骤的查询延迟。
由于特定候选单元格的实际细化时间依赖于查询,直到执行细化步骤后才知道,因此我们希望找到能够准确估计细化时间的指标,或者是预先计算的(即查询独立),或者是在查询时易于计算的指标。论文主要关注四个指标:(a). 帖子数量;(b). 它的扩展区域的帖子数量;(c). 跳跃长度 (d). 它的扩展区域的跳跃长度。论文的实验证明跳跃长度依赖于帖子数量,因此只需要关注(b)和(d)指标。如图 4所示,显然,扩展后的区域的帖子数量与细化时间有更高的相关性,因此论文将其作为估计细化时间的指标。
论文的下一步是选择一种有效的工作负载分配策略来平衡每个集群节点的工作负载。简单的方法是将候选单元随机分配给各个工作节点,以便每个节点获得相似数量的候选单元进行处理。这种方法并不是非常有效,原因是每个候选单元格的细化时间差异很大,因为细化时间与扩展区域内的帖子数量高度相关。相反,我们分配候选单元格给节点时考虑使得每个工作节点有相似的帖子总数。
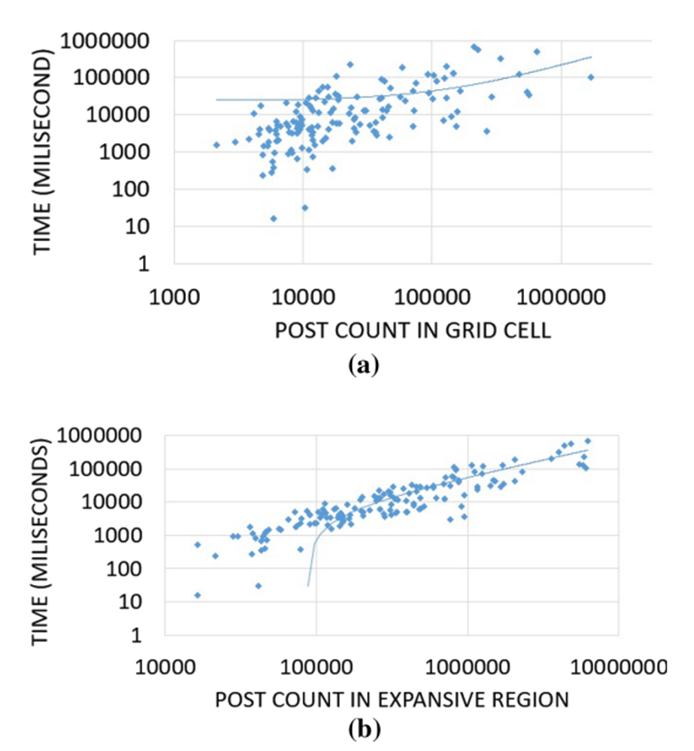
图4 细化步骤与帖子数量的关系
即使实现了完美的负载平衡,并行算法的运行时间也将受到运行时间最长的单元格的限制。在这部分中,论文提出了如何通过切片候选单元来增加并行化粒度以减少单元计算时间的上限。
设G是由查询的过滤步骤提供的候选单元格的集合。论文提出了一种启发式方法,即切片具有高NE(扩展区域的帖子数量)的候选单元格。特别地,每个候选单元格都被分配了一个切片计数s(该单元格的切片数)。设M为集群中的核数。对G中所有单元格的NE求和表示RSK细化步骤所需的工作量。理想情况下,我们希望在所有节点之间平均分配这个工作负载,但这是不可能的,因为每个候选节点的NE都不一样。为了更容易地分发,论文将工作负载划分为γ·M个切片,其中γ是一个常数,表示每个节点的平均切片数量。接下来可以求出每个切片的平均工作负载τ,再用NE/τ计算出节点需要切片的数量。
图 5展示了两种切片方式,(a)是每个切片拥有相同的宽度,(b)是每个切片拥有相同的帖子数量,实验结果表明切片方式(b)更优。
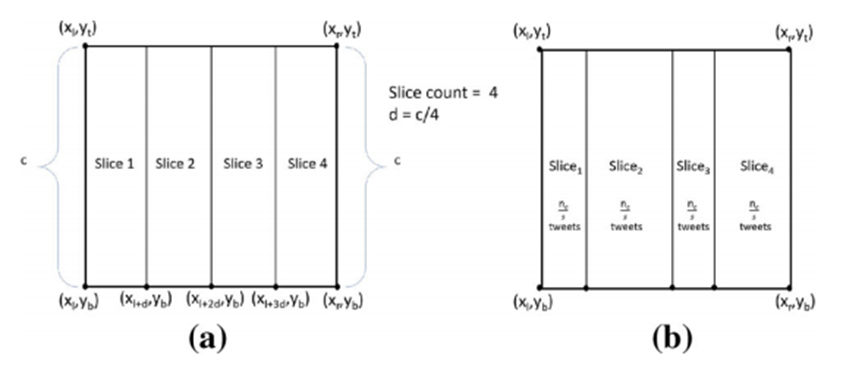
图 5 切片方式
7.实验
论文使用了两个真实数据集:twitter数据集,带有1500万条带有地理标记的推文,平均每条推文有5个关键字;以及芝加哥犯罪数据集:包含700万份犯罪报告,每份报告平均包含两个关键字。
首先来看论文提出的各类方法对RSKR查询的提升,图 6展示了在不同的查询参数k的情况下论文提出的各类算法对查询效率的提升。其中RSK-V是只有水平跳跃的算法,RSK-VH是同时包含水平跳跃和垂直跳跃的算法,RSK-no filter是没有过略步骤的算法。可以看出,水平跳跃的引入极大提升了查询效率,同时,过滤步骤的引入让算法效率提升了1.5-7倍。
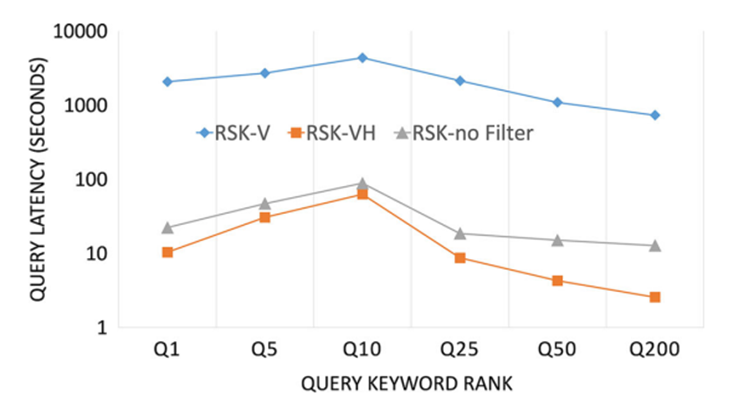
图 6 不同k情况下各类算法查询延迟对比
至于论文提出的网格大小的估计策略,图 7展示了论文得到的网格大小与实验得到的最优网格大小的对比,在不同的查询参数k下,估计的网格大小与实验得到的最优网格大小十分相近。同时,(d)表明在使用估计的网格处理查询时,其效率与实验得到的最优网格的效率相近。
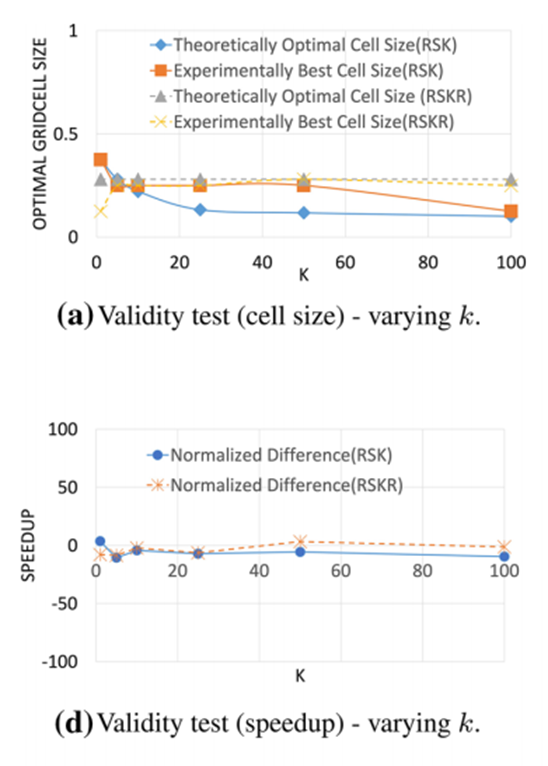
图 7 不同k情况下网格大小与理论最优对比
图 7展示了切片算法对于查询性能的提升,可以看出,论文中提出的工作负载划分策略远优于随机划分的策略,同时,切片可以进一步降低查询延迟。
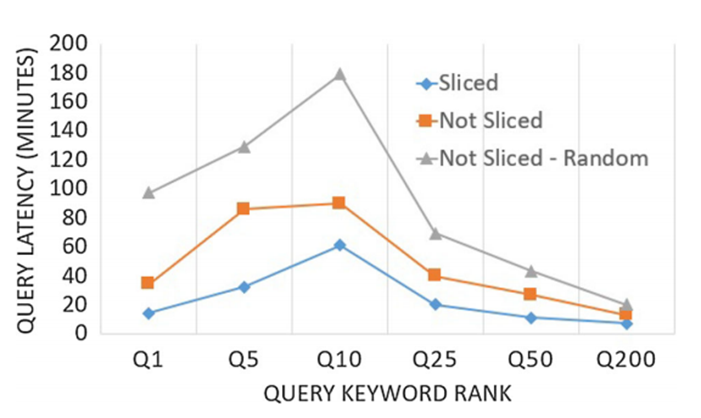
图 8 切片算法的影响
GARNET也研究了RSKR问题,但与论文中不同的是,GARNET限制邻域的大小为网格的大小,同时只有当q是网格的中心点的(k, l)项时才将网格视为答案。图 8展示了在不同的查询参数k的情况下GARNET与论文算法的对比。RSKR-Exact与FS-PC分别为论文对RSKR查询的准确查询算法和估计查询算法。可以看出,GARNET忽略了许多正确的答案,而论文的方法可以检测许多需要的l-square邻域。
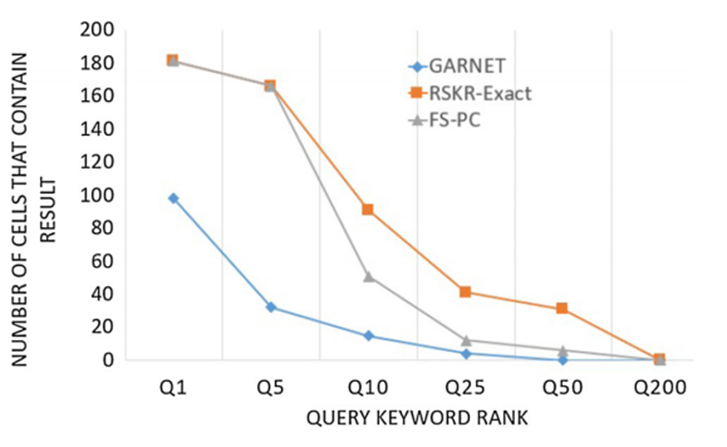
图 9 不同k值下返回单元格个数对比
8.总结与展望
论文对带有地理标记的帖子引入了反向空间关键字(RSK)查询,它允许用户识别特定关键字的流行位置。通过使用术语频率列表(STL),提出了解决RSK查询的算法,并进一步提出了一个限制版本的查询(RSKR),为此提出了一个精确的、多个更快但近似的算法。在两种查询中,论文都提出了并行化策略。一个未来的方向是探索时空数据上的RSK相关查询。
参考文献:
[1].Ahmed P, Eldawy A, Hristidis V, et al. Reverse spatial top-k keyword queries[J]. The VLDB Journal, 2022: 1-24.
[2].Egghe, L.: Untangling Herdan’s law and Heaps’ law: mathematical and informetric arguments. J. Assoc. Inf. Sci. Technol. 58(5), 702–709 (2007). https://doi.org/10.1002/asi.20524
|







