本次为大家介绍国际顶级数据工程会议ICDE 2022上的论文：《Maximizing Range Sum in Trajectory Data》。
一、背景
在智能手机和车辆等支持GPS的移动设备的普及与推广下，基于位置的服务引起了较大的关注；其中，作为基本操作的位置选择查询在最近已被广泛研究。位置选择查询主要有两种：1）检索新设施的位置并在给定设施和客户之间优化指标，例如最佳位置查询；2）旨在搜索具有最大范围权重总和的固定大小区域，例如最大化范围和查询MaxRS是查找一个固定大小的矩形的最佳位置，以最大化二维空间中一组给定加权对象被覆盖的权重总和。
由于MaxRS查询的重要性，在计算机几何和数据库社区中引起了大量的研究工作，例如最优化内存空间且时间复杂度为的算法、I/O高效外部存储器算法、基于采样的近似算法等等。但现有算法通常假定每个对象都与一个唯一点相关联；然而在基于GPS车辆监控等的实际应用中，对象往往是移动的，即为由一系列点构成的轨迹。故如何处理MaxRST查询（基于轨迹数据的MaxRS查询）是一个有待解决的重要问题。
在该篇论文中，主要解决MaxRST查询的两个实质性挑战：
（1）高效并精确求解MaxRST查询。
（2）高效返回具有一定误差的MaxRST查询的近似答案。因为在数据集很大时，返回一个准确答案的效率较低；同时，在一些实际场景中，用户可以放弃一定程度的精确性来缩短响应时间。
该篇论文的主要贡献是：
（1）将MaxRST查询（轨迹数据的MaxRS查询）的问题形式化，将覆盖的概念拓展到轨迹数据。
（2）提出一种基于区间树的分区技术来解决直线多边形相交问题；MaxRST查询可以简化为直线多边形相交问题。
（3）提出两种互补的基于采样的方法，以在理论上保证近似求解MaxRST查询。
二、问题表示
概念：覆盖。给定在二维空间下的一个轨迹T和一个矩形r，T被r覆盖当且仅当T中只要有一个点被r覆盖。令Tr是被r覆盖的轨迹集合。
概念：MaxRST查询。给定在二维空间下的一个加权轨迹T和一个固定大小为a×b的查询矩形r。MaxRST查询就是在该二维空间下找到矩形r的位置使得被覆盖的轨迹权重最大，即
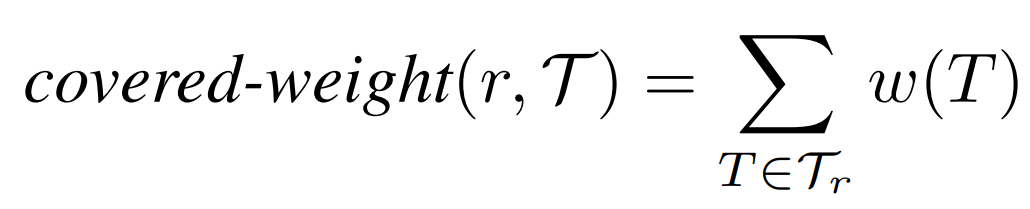
显然，MaxRS查询是MaxRST查询的特例，即每个轨迹只包含一个点。
三、精确算法PMaxRST
MaxRST查询的一个直观方法是详尽地检查平面空间中所有可能的矩形。但时，可能的矩形数为O(n2)，每个矩形的识别成本为O(n)，故这种方法需要O(n3)的时间复杂度，效率极低。
在该篇论文中，提出一种新颖的高效算法，将MaxRST查询转换为直线多边形相交问题，然后利用分区技术加速直线多边形相交问题的计算，使得最终的时间复杂度为（其中n是轨迹集中点的数量总和）。
1. 问题转换
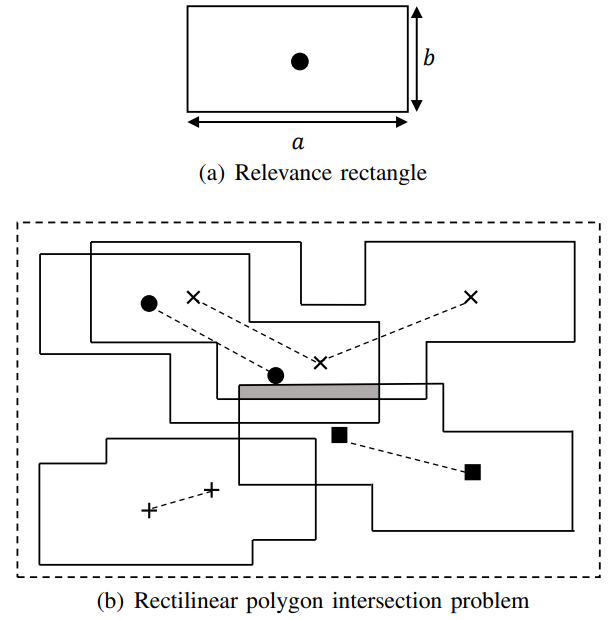
给定一点p=(x, y)，则点p对应的矩形Rp为[x – a 2, x + a / 2] × [y – b / 2, y + b / 2], 如上图图（a）所示。一条轨迹中每个点的对应矩形可以组合成一个直线多边形。
MaxRST查询可以转换为直线多边形相交问题。在上图图（b）中，若每条轨迹的权重是1，则在阴影区的点p是直线多边形相交问题的最优解，因为覆盖它的直线多边形的权重和（即轨迹权重和）最大。
2. 分区技术
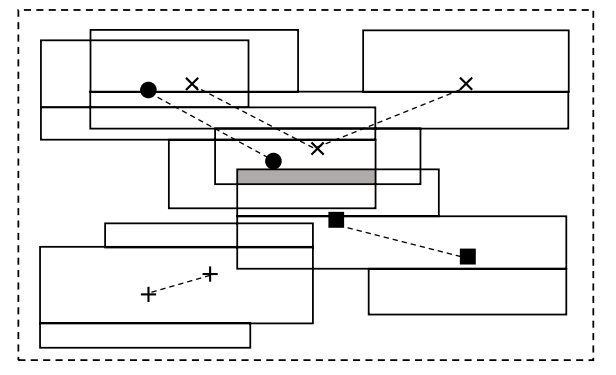
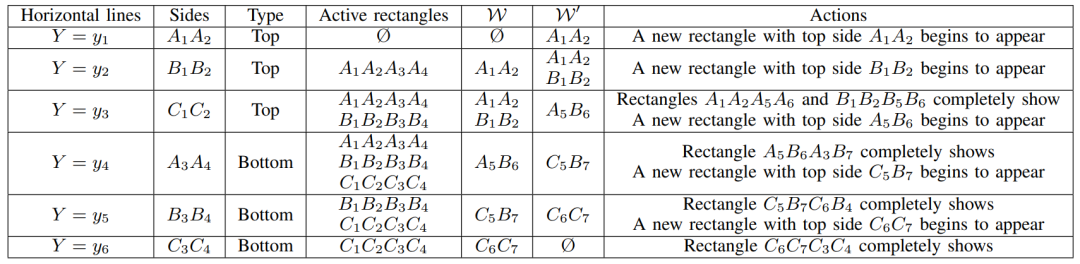
分区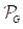
是加权几何G的一个带有w(G)权重的划分。直线多边形G可以分为几个不相交的子区域。上图图（b）中4个直线多边形的交集问题可以转换下图中13个水平分割矩形问题。
可以观察到，任何直线多边形都可以划分为几个不相交的矩形，其数量与直线多边形中角点的数量成线性比例。因此，我们只需要解决这些分区矩形的交集问题。幸运的是，已经存在着在O(n log n)时间下解决直线多边形相交问题的现有方法。
3. 利用区间树的高效分区方法
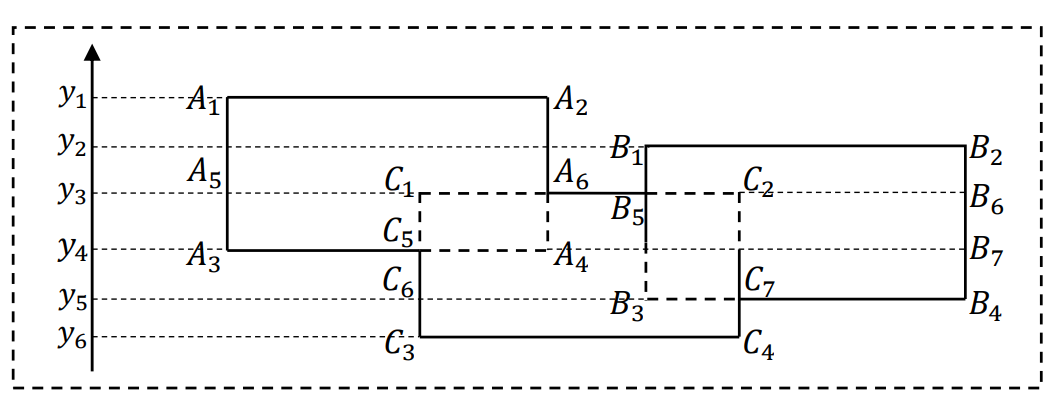
论文提出的分区方法的关键思想是采用平面扫描策略，用水平线从上到下扫描平面，水平扫描线的位置仅由相关矩形的水平边按顺序决定。显然，要处理的水平扫描线的数量最多是相关性矩形的两倍，因为每个相关性矩形都有两条水平边（即顶部和底部）。如果水平扫描线已处理其顶部但尚未到达其底部，则矩形处于活动状态。
窗口是由矩形组成的区域所包含的最大水平间隔。实际上，分区不相交矩形的水平边必须是窗口。
在平面扫描的过程中，我们需要动态更新当前窗口。给定轨迹T和大小为a×b查询矩形，分区算法的基本流程如下：
（1）对于每一个点p=(x,y)∈T，以p为中心的相关矩形Rp大小为a×b，该矩形有顶部和底部两条水平边。
（2）将所有相关矩形的水平边按其Y坐标降序排序，并按顺序处理每一边Sp。如果Sp是顶部，则执行步骤3；若Sp是底部，则执行步骤4。
（3）若Sp是顶部，当水平扫线遇到时会有3种情况：
1）若当前处理边Sp在更新窗口中，则没有新分区矩形；
2）若当前处理边Sp不在更新窗口中，则出现新分区；
3）若当前处理边Sp与更新窗口中某个窗口重叠但不相互包含，则老分区矩形R0完全出现且新分区矩形Rn开始出现。如出现该情况，需要将分区矩形合并成长条矩形。
而这三种情况，都需要遍历当前窗口中的所有活动矩形来判断，但这是低效的。基于此，论文提出利用区间树来替代遍历窗口中所有矩形的方法。首先令矩形Ri被设置为活动并将Si插入区间树中，再根据插入的结果更新当前窗口。
（4）若Sp是底部，与顶部一样分为相应的3种情况。同样，也利用区间树区间节点的删除和窗口的更新。
例如，给定一个具有3个点的轨迹以及相应的矩形，其区间算法流程如下图所示。
4. 区间树
区间树是一个平衡的二叉树。令{x1,x2,…,xnT}是给定轨迹T按x坐标升序的点，再对{x1-a/2,x1+a/2,x2-a/2, x2+a/2,…,xnT-a/2,xnT+a/2}进行升序排序用于以从左到右的方式初始化区间树的叶节点。对于每个内部节点N，令{x1’,x2’,…,xw’}是以N为根节点的子树种从左到右的叶节点，并有以下属性：
（1）结点N的权重是
（2）{x1’,x2’,…,x[w/2]’}和{ x[w/2]+1’, x[w/2]+2’,…, xw’}分别是N结点左右子树的叶节点
（3）结点N有一个区间列表L，每个区间[lI,rI]∈L都满足lI≤v(N)≤rI
在平面扫描之前，需要创建一个包括总叶和内部节点的基本区间树。此外，每个区间列表都初始化为null。
为了简化说明，令PathN、PathNL、PathNR分别表示根节点到内部节点N、内部节点N到值为lI的叶节点、内部节点N到值为rI的叶节点。
插入：在平面扫描中，若水平扫描线与相关矩形的顶部I=[lI,rI]相遇时，将区间I以自上而下的方式插入到区间树中，知道内部节点N满足lI≤v(N)≤rI，再将区间I=[lI,rI]到N节点对应的区间列表中。从值分别为和的叶节点以自下而上的方式搜索区间树，这左右两天搜索路径一定会在N节点汇合。同时，将当前窗口更新。
删除：在平面扫描中，若水平扫描线与相关矩形的底部I=[lI,rI]相遇时，以自上而下的方式从区间树中删除区间I=[lI,rI]。然后再继续搜寻PathN、PathNL和PathNR，判断当前窗口和I的关系，并将当前窗口更新。
基于区间树，有定理3：给定一个有节点N和N’的区间树，节点的区间为I=[lI,rI]和I’=[lI’,rI’]。若I’=[lI’,rI’]与I=[lI,rI]相交，则节点N’一定在路径PathN、PathNL和PathNR中。该定理表明所有与I=[lI,rI]相交的区间都可以在路径PathN、PathNL和PathNR中找到，基于此，可以判定I和当前窗口的关系。
四、近似算法
(ϵ, δ)-近似MaxRST查询返回具有相对误差ϵ、至少以概率δ达到精确解的近似解。其中，δ是置信度。抽样方法Sampling以相同概率从原轨迹集的直线多边形集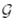
中抽取k个样本，得到样本集
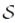。 (ϵ, δ)-近似MaxRST查询的目标是用
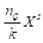去估计准确答案
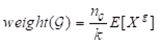。通过系列证明推到可得，给定ϵ(0< ϵ<1)和δ(0<δ<1)，样本大小k的边界为
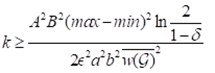（其中，a、b是查询区域的长和宽；max，min是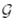中元素的最大权重和最小权重）。即当
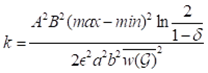时，抽样样本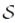的最优解有至少δ的概率为(ϵ,δ)-近似MaxRST查询的目标答案。
基于此，我们可以用抽样的方法来近似最优解——首先对轨迹集里所有轨迹标号，并进行k次独立重复的随机抽取轨迹得到样本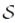，在对样本进行求最优解。这样的话，算法的时间复杂度为
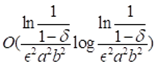，与原始轨迹集的大小无关。
当查询矩形的大小a×b远小于边界大小A×B时，样本数量大小会特别大，甚至比还大。这会限制前一种近似计算应用的范围。基于此，论文又提出了第二种抽样法方法，采样网格偏移技术，使得样本数量大小k从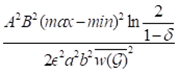
进一步减少为
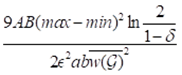。另外，需要额外的O(n)的时间来进行网格创建。
网格 ((x0, y0)-Grid(w,h))是以点(x0, y0)为中心，以w, h为长宽进行网格的划分。单元格是由相邻的水平网格线和垂直网格线所包围成的矩形。如下图所示，w = 2a, h = 2b，其中的灰色矩形是一个单元格。
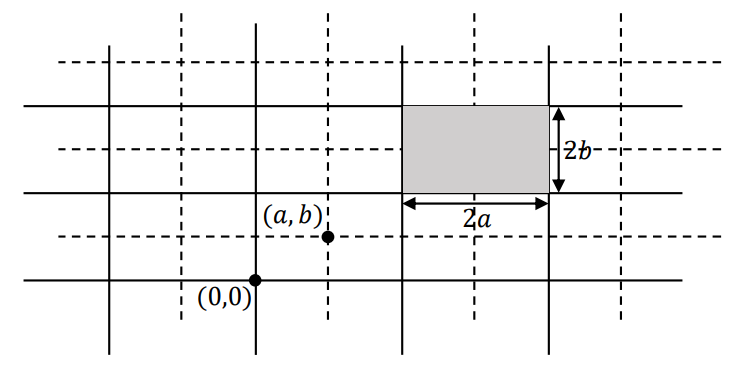
令G0, G1, G2,G3分别表示(0, 0) - Grid(2a,2b), (0, a) -Grid(2a, 2b), (0,b) - Grid(2a,2b), (a, b)-Grid(2a,2b)。G1, G2, G3可以由G0移动得到。如上图所示，G0是实线网格，G3是虚线网格。显然，在G0, G1, G2,G3中，一定存在一个单元格完全包含了a×b区域的MaxRST查询的最优矩形。因此，轨迹在G0, G1, G2, G3这四个网格获得的最大的MaxRST结果是MaxRST查询的最优解。
对于每个单元格c，单元格c内轨迹点的相应直线多边形所构成的边界最大为3a×3b。因此，在单元格c中样本大小k的边界为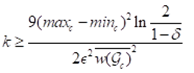
,其中，
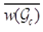是单元格c中轨迹的平均权重，maxc和minc是单元格c中最大和最小权重。
基于此，当样本数量大小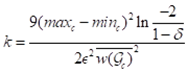
时，抽样样本的最优解有至少δ 的概率为单元格c的精确查询值。在G0, G1, G2, G3每个网格中，非空单元格最多为
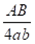。因此，寻找全局MaxRST最优解的时间
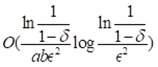。而用哈希构建网格需要O(n)的时间。故这种基于网格偏移的采样方法的时间复杂度
。
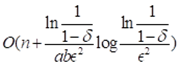五、实验
1. 实验设置
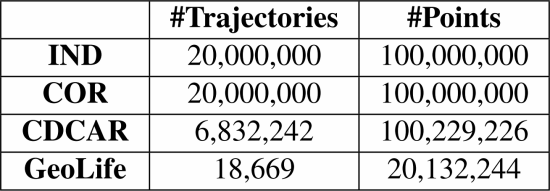
实验数据集。两种符合独立且相关分布的合成数据集IND和COR。这两个数据集都有20,000,000条轨迹和100,000,000个点。
两个真实的数据集CDCAR和GeoLife。CDCAR包含滴滴出行所收集的中国成都的汽车轨迹，共6,832,242条。GeoLife包含了中国背景境内2007年4月至2012年8月的用户轨迹，共18,669条。
对于每条轨迹，在[1,100]范围内均匀地生成其权重。
2. 运行时间
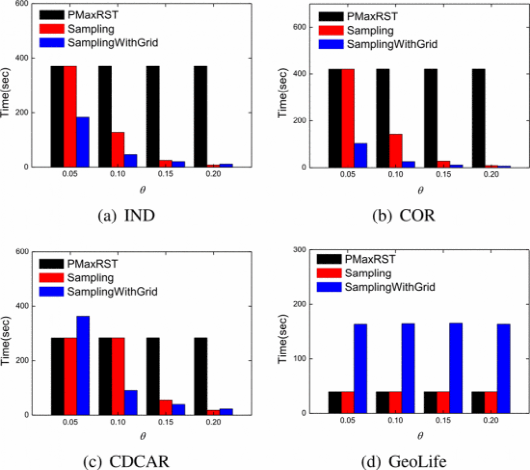
轨迹数量的影响。由下图图(a)和图(b)所示，两种近似算法Sampling和SamplingWithGrid的时间与轨迹数无关。但也有特殊情况，即需要采样的轨迹数量大于原数据集的数量大小。实验表明，精确算法MaxRST在效率和可扩展性方面具有较高性能，计算算法Sampling和SamplingWithGrid更适用于大型轨迹数据集。
相对误差的影响。如下图所示，近似算法Sampling和SamplingWithGrid受查询矩形大小的影响较大。随着相对相对误差ε的变化，近似算法Sampling和SamplingWithGrid都具有二次下降趋势。
查询矩形大小的影响。可以通过参数θ改变查询矩形大小。如下图所示，Sampling和SamplingWithGrid受查询矩形大小的影响较大。Sampling具有四次趋势，SamplingWithGrid具有二次趋势。另外，由于GeoLife数据集中的轨迹数据量最少，Sampling和SamplingWithGrid的性能都较差。
六、总结
论文将覆盖的概念扩展到轨迹数据，提出MaxRST查询的定义。然后，将MaxRST查询转换为直线多边形相交问题，并开发一种利用区间树的分区算法来解决精确该问题。此外，还提出两种互补的基于采样的(ϵ,δ)-近似MaxRST查询，返回具有相对误差
、至少以概率δ达到精确解的近似解：1）第一种采样方法对直线多边形执行随机抽样和替换；2）第二种采样方法是利用网格位移技术来减少样本量，但需要额外的网格构建的时间成本。同时，通过理论和实验结果表明，论文所提的算法在效率和精度方面既有较高的性能。
-End-
| 本文作者 吴怡 重庆大学计算机科学与技术（卓越）专业在读大三学生，重庆大学START团队成员，主要研究方向：时空数据管理与挖掘。 |
时空艺术团队（START，Spatio-Temporal Art）来自重庆大学时空实验室，旨在发挥企业和高校的优势，深入探索时空数据收集、存储、管理、挖掘、可视化相关技术，并积极推进学术成果在产业界的落地！年度有2~3名研究生名额，欢迎计算机、GIS等相关专业的学生报考！
