第6章 数据分析——6.1 多项式及其函数

知识要点

数据分析和处理是各种应用中非常重要的问题。针对数据分析和处理，MATLAB提供了大量的函数，方便用户使用。本章将介绍MATLAB强大的数据分析和处理功能，首先介绍多项式函数，这些函数用于多项式求值、多项式乘法、多项式除法等；接着介绍插值函数，MATLAB提供数个不同的插值算法；最后介绍limit函数对数组和函数极限的求解过程。

学习要求

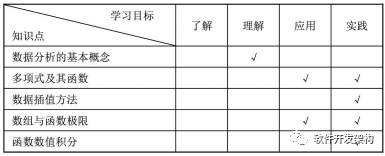
多项式作为线性方程组的表现形式，在运算及应用中具有非常重要的意义，本节将重点介绍多项式的各种运算法则、运算函数及操作指令，并特别对有理多项式进行说明。

6.1.1  多项式的表达式和创建

MATLAB中使用一维向量来表示多项式，将多项式的系数按照降幂次序存放在向量中。多项式P(x)的具体表示方法如下：

P(x)=a₀xⁿ +a₁x^n-1+a_n-1x+a_n的系数构成的向量为：[ a₀a₁… a_n-1a_n ]。

例如，多项式2x⁴+3x³+5x²+1就可以用向量[2 3 5 0 1]来表示。应当注意的是，多项式中缺少的幂次的系数应当为“0”。在MATLAB中，多项式由一个行向量表示，它的系数是按降序排列的。

例6-1：输入多项式3x⁴-10x³+15x+1000。

在命令行窗口中输入：

p = [3 -10 0 15 1000]

输出结果：

p =

           3         -10           0          15        1000

注意：必须包括具有0系数的项，如在上例中，多项式并没有二次项，因此二次项的系数为0，否则MATLAB是无法知道哪一项为0的。

例6-2：将向量表示的多项式用字符串输出的通用函数示例。

创建M文件并命名为ex6_02.m，利用M文件编辑器在M文件中输入：

function s = pprintf(p)

if nargin > 1

    error ('Too much input arguments ')     % 确认输入变量

end

while p(1) == 0         % 将高次的零去掉

    p(1) = [];

end

l = length(p);          % 计算p的长度

if l == 0

    s = '0';

elseif l == 1

    s = num2str(p(1));

elseif l == 2

    s = strcat(num2str(p(1)), 'x+', num2str(p(2)));

elseif l > 2

    for i = 1 : l

        if i == 1

            if p(i) == 1

                s = strcat('x^{', num2str(l - i), '}');

            else

                s = strcat(num2str(p(i)), 'x^{', num2str(l - i), '}');

            end

        elseif i == l

            s = strcat(s, '+', num2str(p(i))');

        elseif i == l - 1

            s = strcat(s, '+', num2str(p(i)), 'x');

        else

            if p(i) == 0

            else

                s = strcat(s, '+', num2str(p(i)), 'x^{', num2str(l - i), '}');

            end

        end

    end

end

现在，为了试验函数pprintf，在命令行窗口中输入：

p = [1 0 3 5 7 9];

figure; title(pprintf(p))

在图形界面上输出结果：

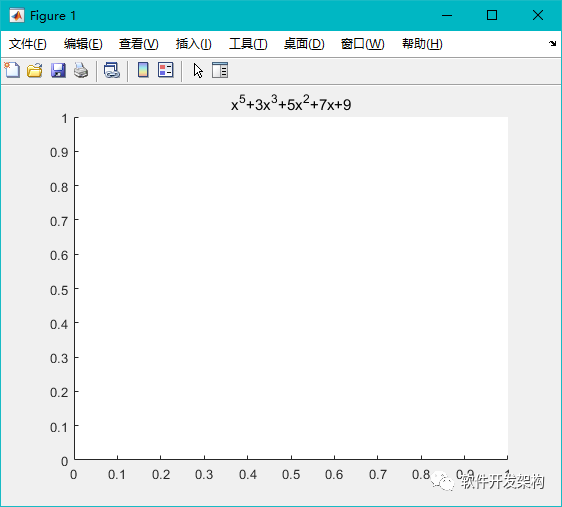
6.1.2  多项式求根

1．多项式的根

找出多项式的根，即使多项式为0的值，可能是许多学科共同的问题。MATLAB能求解这个问题，并提供了特定函数roots求解一个多项式的根。

例6-3：求解多项式3x⁴-10x³+15x+1000的根。

在命令行窗口中输入：

p = [3 -10 0 15 1000];

r = roots(p)

输出结果：

r =

   4.0283 + 2.8554i

   4.0283 - 2.8554i

  -2.3616 + 2.8452i

  -2.3616 - 2.8452i

2．由根创建多项式

在MATLAB中，无论是一个多项式还是它的根，都是以向量形式存储的。按照惯例，多项式是行向量，根是列向量。因此，当我们给出一个多项式的根时，MATLAB也可以构造出相应的多项式，这个过程需要使用函数poly。

例6-4：由根创建多项式。

在命令行窗口中输入：

r = [4.0283 + 2.8554i;4.0283 - 2.8554i;-2.3616 + 2.8452i;-2.3616 - 2.8452i];

p = poly(r)

输出结果：

p =

    1.0000   -3.3334   -0.0001    5.0016  333.3381

因为MATLAB无隙地处理复数，当用根重组多项式时，如果一些根有虚部，由于截断误差，则poly的结果有一些小的虚部。消除虚假的虚部，只要使用函数real抽取实部即可。

6.1.3  多项式的四则运算

1．多项式的加法

对于多项式的加法，MATLAB并未提供一个特别的函数。如果两个多项式向量大小相同，那么多项式相加时就与标准的数组加法相同。

例6-5：多项式加法运算示例一。

在命令行窗口中输入：

a = [1 3 5 7 9];

b = [1 2 4 6 8];

c = a + b

输出结果：

c =

     2     5     9    13    17

结果是c(x)=2x⁴+5x³+9x²+13x+17。

注意：当两个多项式阶次不同时，低阶的多项式用首零填补，使其与高阶多项式有同样的阶次。要求首零而不是尾零，是因为相关的系数像x幂次一样，必须整齐。

例6-6：多项式加法运算示例二。

在命令行窗口中输入：

a = [1 3 5 7 9];

b = [0 2 4 6 8];

c = a + b

输出结果：

c =

     1     5     9    13    17

结果是c(x)=x⁴+5x³+9x²+13x+17。

有的时候，两个相加的多项式的项数并不明确，这时可用一个文件编辑器创建一个通用的多项式相加函数M文件来执行一般的多项式加法。

例6-7：通用的多项式加法函数示例。

创建M文件并命名为ex6_07.m，利用M文件编辑器在M文件中输入：

function p = ppadd(a, b)

if nargin < 2

    error('Not enough input arguments')     % 确认输入变量

end

a = a(:).';             % 将输入转化为行向量

b = b(:).';

na = length(a);         % 求相加的两个多项式的项数

nb = length(b);

% 当相加的两个多项式项数不等时，高次补零

p = [zeros(1, nb - na) a] + [zeros(1, na - nb) b];

现在，为了试验函数ppadd，在命令行窗口中输入：

a = [1 3 5 7 9];

b = [0 2 4 6 8];

c = ppadd(a, b)

输出结果：

c =

     1     5     9    13    17

结果是c(x)= x⁴+5x³+9x²+13x+17。

2．多项式的乘法

在MATLAB中，函数conv支持多项式乘法（运算法则为执行两个数组的卷积）。

例6-8：多项式乘法运算示例。

在命令行窗口中输入：

a = [1 3 5 7 9];

b = [1 2 4 6 8];

c = conv(a, b)

输出结果：

c =

     1     5    15    35    69   100   118   110    72

结果是c(x)=x⁸+5x⁷+15x⁶+35x⁵+69x⁴+100x³+118x²+110x+72。

3．多项式的除法

在一些特殊情况下，一个多项式需要除以另一个多项式。在MATLAB中，这是由函数deconv完成的。

例6-9：多项式除法运算示例。

在命令行窗口中输入：

c = [1 5 15 35 69 100 118 110 72];

b = [1 2 4 6 8];

[a, r] = deconv(c, b)

输出结果：

a =

     1     3     5     7     9

r =

     0     0     0     0     0     0     0     0     0

a是多项式c除以多项式b的商，余式为r。本例中r为零多项式，因为多项式b和多项式a的乘积恰好是c。

6.1.4  多项式的导数、积分与估值

1．多项式的导数

MATLAB为多项式求导提供了函数polyder。

例6-10：多项式求导运算示例。

在命令行窗口中输入：

d = [1 5 15 35 69 100 118 110 72];

e = polyder(d)

输出结果：

e =

     8    35    90   175   276   300   236   110

2．多项式的积分

MATLAB为多项式的积分提供了函数polyint，其具体的调用格式如下。

● polyint(P,k)：返回多项式P的积分，积分常数项为k。

● polyint(P)：返回多项式P的积分，积分常数项默认值为0。

例6-11：多项式积分运算示例。

在命令行窗口中输入：

d = [1 5 15 35 69 100 118 110 72];

f = polyint(d)

输出结果：

f =

  列 1 至 8

    0.1111    0.6250    2.1429    5.8333   13.8000   25.0000   39.3333   55.0000

  列 9 至 10

   72.0000         0

3．多项式的估值

根据多项式系数的行向量，可对多项式进行加、减、乘、除和求导运算，也能对它们进行估值。在MATLAB中，这由函数polyval来完成。

例6-12：多项式的估值运算示例。

在命令行窗口中输入：

x = -1 : 0.01 : 1;      % 生成自变量

g = [1 3 5 7 9];        % 函数对应的多项式

h = polyval(g, x);      % 进行估值运算

% 将估值运算结果对自变量作图

plot(x, h);

xlabel('x');

title('x^4 + 3x^3 + 5x^2 + 7x + 9');

输出结果如图6-1所示。

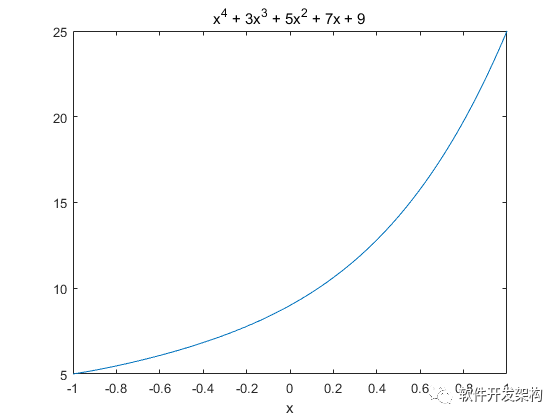
图6-1  多项式估值运行结果

6.1.5  多项式运算函数及操作指令

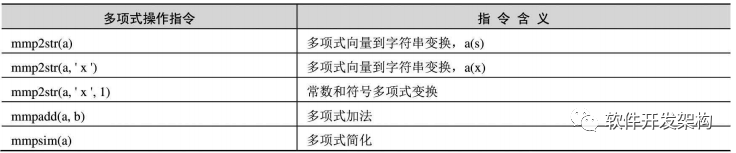
多项式的运算函数及常用的操作指令如表6-1和表6-2所示。

表6-1  多项式运算函数

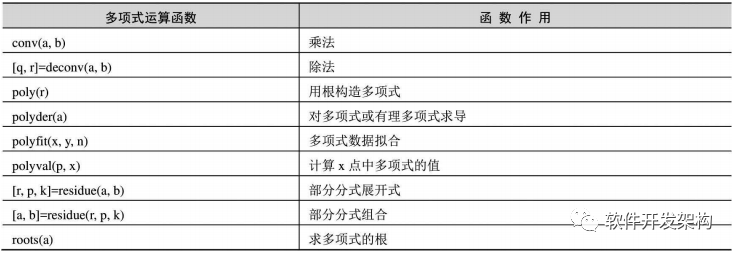
表6-2 多项式操作指令

6.1.6  有理多项式

在许多应用中，例如在傅里叶（Fourier）、拉普拉斯（Laplace）和Z变换中，出现了两个多项式之比。在MATLAB中，有理多项式由它们的分子多项式和分母多项式表示。对有理多项式进行运算的两个函数是residue和polyder。函数residue执行部分分式展开的运算。

例6-13：有理多项式的展开。

在命令行窗口中输入：

num = [5 3 -2 7];       % 分子多项式

den = [-4 0 8 3];       % 分母多项式

[r, p, k] = residue(num, den)

输出结果：

r =

   -1.4167

   -0.6653

    1.3320

p =

    1.5737

   -1.1644

   -0.4093

k =

   -1.2500

本例结果可表示成：

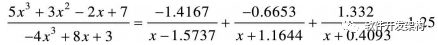
residue函数也可执行逆运算。

例6-14：有理多项式展开的逆运算。

在命令行窗口中输入：

num = [5 3 -2 7];       % 分子多项式

den = [-4 0 8 3];       % 分母多项式

[r, p, k] = residue(num, den);

[n, d] = residue(r, p, k)

输出结果：

n =

   -1.2500   -0.7500    0.5000   -1.7500

d =

    1.0000   -0.0000   -2.0000   -0.7500

本例结果可表示成：

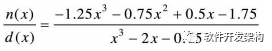
函数polyder可用来对多项式求导。除此之外，如果输入两个多项式，则polyder函数对两个多项式构成的有理多项式求导。

例6-15：有理多项式的求导。

在命令行窗口中输入：

num = [5 3 -2 7];       % 分子多项式

den = [-4 0 8 3];       % 分母多项式

[b, a] = polyder(num, den)

输出结果：

b =

    12    64   153    18   -62

a =

    16     0   -64   -24    64    48     9