矩阵的加、减、乘、除、比较运算和逻辑运算等代数运算是MATLAB数值计算最基础的部分。本节将重点介绍这些运算。
3.3.1 矩阵的加减法运算
进行矩阵加法、减法运算的前提是参与运算的两个矩阵或多个矩阵必须具有相同的行数和列数，即A、B、C等多个矩阵均为m×n矩阵；或者其中有一个或多个矩阵为标量。
在上述前提下，对于同型的两个矩阵，其加减法定义如下：
C = A ± B，矩阵C的各元素Cmn = Amn ± Bmn。
当其中含有标量x时，
C = A ± x，矩阵C的各元素Cmn = Amn ± x。
由于矩阵的加法运算归结为其元素的加法运算，容易验证，因此矩阵的加法运算满足下列运算律。
（1）交换律：A+B=B+A。
（2）结合律：A+(B+C)=(A+B)+C。
（3）存在零元：A+0=0+A=A。
（4）存在负元：A+(-A)=(-A)+A。
例3-25：矩阵加减法运算示例。
已知矩阵A=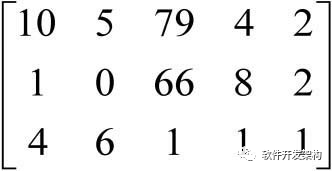 
，矩阵B= 
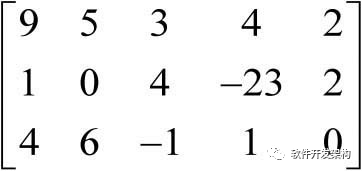，行向量C= [2 1]，标量x=20，试求A + B、A - B、A + B + x、A - x、A - C。
在命令行窗口中依次输入：
A = [10 5 79 4 2; 1 0 66 8 2;4 6 1 1 1];
B = [9 5 3 4 2;1 0 4 -23 2;4 6 -1 1 0];
C = [2 1];
x = 20;
ApB = A + B
AmB = A - B
ApBpm = A + B + x
Amx = A - x
AmC = A - C
得到的结果为：
ApB =
19 10 82 8 4
2 0 70 -15 4
8 12 0 2 1
AmB =
1 0 76 0 0
0 0 62 31 0
0 0 2 0 1
ApBpm =
39 30 102 28 24
22 20 90 5 24
28 32 20 22 21
Amx =
-10 -15 59 -16 -18
-19 -20 46 -12 -18
-16 -14 -19 -19 -19
矩阵维度必须一致。
在A-C的运算中，MATLAB返回错误信息，并提示矩阵的维度必须一致。这也证明了矩阵进行加减法运算必须满足一定的前提条件。
3.3.2 矩阵的乘法运算
MATLAB中矩阵的乘法运算包括两种：数与矩阵的乘法；矩阵与矩阵的乘法。
1．数与矩阵的乘法
由于单个数在MATLAB中是以标量来存储的，因此数与矩阵的乘法也可以称为标量与矩阵的乘法。
设x为一个数，A为矩阵，则定义x与A的乘积C=xA仍为一个矩阵，C的元素就是用数x乘矩阵A中对应的元素而得到的，即Cmnx=xAmn。数与矩阵的乘法满足下列运算律：
● 1A=A。
● x(A+B)=xA+xB。
● (x+y)A=xA+yA。
● (xy)A=x(yA)=y(xA)。
例3-26：矩阵数乘示例。
已知矩阵A= 
，E是3阶单位矩阵，E= 
，试求表达式2A+3E。
在命令行窗口中依次输入：
A = [0 3 3;1 1 0;-1 2 3];
E = eye(3);
R = 2 * A + 3 * E
得到结果：
R =
3 6 6
2 5 0
-2 4 9
2．矩阵与矩阵的乘法
两个矩阵的乘法必须满足被乘矩阵的列数与乘矩阵的行数相等。设矩阵A为m×h矩阵，B为h×n矩阵，则两个矩阵的乘积C=A×B为一个矩阵，且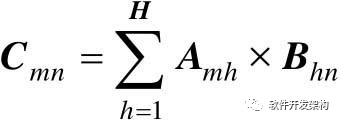
。
矩阵之间的乘法不遵循交换律，即A×B≠B×A。但矩阵乘法遵循下列运算律。
● 结合律：(A×B)×C=A×(B×C)。
● 左分配律：A×(B+C)=A×B+A×C。
● 右分配律：(B+C)×A=B×A+C×A。
● 单位矩阵的存在性：E×A=A，A×E=A。
例3-27：矩阵乘法示例。
已知矩阵A=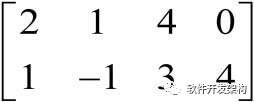 
，矩阵B=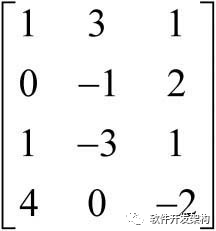
，试求矩阵乘积AB及BA。
在命令行窗口中依次输入：
A = [2 1 4 0;1 -1 3 4];
B = [1 3 1;0 -1 2;1 -3 1;4 0 -2];
R1 = A * B
R2 = B * A
得到结果：
R1 =
6 -7 8
20 -5 -6
错误使用 *
用于矩阵乘法的维度不正确。请检查并确保第一个矩阵中的列数与第二个矩阵中的行数匹配。要执行按元素相乘，请使用 '.*'。
3.3.3 矩阵的除法运算
矩阵的除法是乘法的逆运算，分为左除和右除两种，分别用运算符号“\”和“/”表示。A\B表示矩阵A的逆乘以矩阵B，A/B表示矩阵A乘以矩阵B的逆。除非矩阵A和矩阵B相同，否则A/B和A\B是不等价的。对于一般的二维矩阵A和B，当进行A\B运算时，要求A的行数与B的行数相等；当进行A/B运算时，要求A的列数与B的列数相等。
例3-28：矩阵的除法运算示例。
设矩阵A= 
，矩阵B= 
，试求A\B和A/B。
在命令行窗口中依次输入：
A = [1 2 ; 1 3];
B = [1 0 ; 1 2];
R1 = A\B
R2 = A/B
得到结果：
R1 =
1 -4
0 2
R2 =
0 1.0000
-0.5000 1.5000
3.3.4 矩阵的幂运算
当矩阵A为方阵时，可进行矩阵的幂运算，其定义为：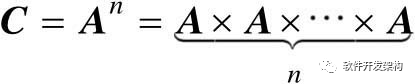 
。在MATLAB中，使用运算符号“^”表示幂运算。
例3-29：方阵幂运算示例。对于给定方阵A= 
，试求A2、A5。
在命令行窗口中依次输入：
A = [2 3 8;3 1 -1;5 0 4];
A2 = A ^ 2
A5 = A ^ 5
得到结果：
A2 =
53 9 45
4 10 19
30 15 56
A5 =
37496 13827 52622
10077 2887 11891
34295 11250 44464
3.3.5 矩阵元素的查找
MATLAB中函数find()的作用是进行矩阵元素的查找，它通常与关系函数和逻辑运算相结合。其调用格式如下。
● ind=find(X)：该函数查找矩阵X中的非零元素，函数返回这些元素的单下标。
● [row,col]=find(X,...)：该函数查找矩阵X中的非零元素，函数返回这些元素的双下标i和j。
例3-30：利用函数find()查找矩阵中的元素示例。
在命令行窗口中依次输入：
clear all;
A = [1 3 0;3 1 0;9 2 4]
B = find(A) % 矩阵中非零元素的下标
C = find(A >= 1) % 矩阵中大于或等于1的元素的下标
D =A(A >= 1) % 矩阵中大于或等于1的元素
BCD = [B,C,D]
A(find(A == 0)) = 10 % 将矩阵中等于0的元素改为10
输出结果：
A =
1 3 0
3 1 0
9 2 4
B =
1
2
3
4
5
6
9
C =
1
2
3
4
5
6
9
D =
1
3
9
3
1
2
4
BCD =
1 1 1
2 2 3
3 3 9
4 4 3
5 5 1
6 6 2
9 9 4
A =
1 3 10
3 1 10
9 2 4
