2.2.6 矩阵的保存和加载
设有矩阵
，现用户希望将元素1修改成-1，并将5、6、8、9这几个矩阵元素以0替代，之后在原始矩阵的最后添加一行，使得新的矩阵A满足某方面的使用要求。因此，用户首先要通过一定的途径让MATLAB找到元素“1”及元素区域“5、6、8、9”，接着对这些矩阵元素的值进行修改，最后增加一行。上述几个方面构成了矩阵元素的基本操作。
本节将介绍矩阵在MATLAB中的存储方式，接着介绍矩阵元素的寻址方法，最后介绍矩阵元素的赋值及扩展与删除。
本节的重点在于让用户理解MATLAB存储矩阵的方法，进而掌握矩阵元素的寻址方法。
1．矩阵在MATLAB中的存储方式
设有矩阵
，用户可以通过在MATLAB的命令行窗口中直接输入矩阵元素来创建此矩阵：
A = [1 0 -1;2 4 9;-5 3 0]
命令行窗口输出如下信息：
A =
1 0 -1
2 4 9
-5 3 0
事实上，MATLAB并不是按照其命令行输出的格式将矩阵A存储在内存空间中的。我们可以把内存空间想象成一列网格，如下所示。
MATLAB将矩阵元素按列优先排列的原则依次放置在相应的格子内，因此，可以将其看成一个长列向量，即
例如，矩阵第2行第2列的元素“4”，实际上位于存储空间第5个格子的位置上。由此，MATLAB采用了两种矩阵元素寻址方法：①矩阵下标寻址；②线性寻址。
2．矩阵元素的寻址方法
1）矩阵下标寻址
在MATLAB中，使用A(i,j)来表示一个矩阵A从左上角数起第i行、第j列的元素，这就是矩阵下标寻址方法。这种方法和线性代数中矩阵元素的引用方法一致，通俗易懂。以下分别介绍利用矩阵下标寻址方法访问矩阵中的单个元素和元素区域。
（1）单个矩阵元素的访问。
当使用双下标访问二维矩阵中的某个元素时，必须同时指定该元素所在的行号和列号，访问格式为：
A(numRow,numColumn)
其中，numRow和numColumn分别代表行号和列号。
例2-45：单个矩阵元素的访问示例。
利用rand函数创建一个4×3的0～1均匀分布的随机数矩阵A并访问其中的元素。在命令行窗口中依次输入：
A = rand(4,3)
x = A(2,2)
y = A(4,3)
得到的结果为：
A =
0.0975 0.9649 0.4854
0.2785 0.1576 0.8003
0.5469 0.9706 0.1419
0.9575 0.9572 0.4218
x =
0.1576
y =
0.4218
（2）矩阵元素区域的访问。
访问矩阵的多个元素，可以是某一行、某一列或者其中的部分元素，也可以是矩阵中的某一块区域。在MATLAB中，元素区域的访问需要用冒号“:”来表示矩阵中的多个元素，具体的访问格式如下。
● A(1:m,n)：表示访问第n列的第一个元素至第m个元素。
● A(m,:)：表示访问第m行的所有元素。
● A(i:j,m:n)：表示访问从第i行至第j行、从第m列至第n列的矩阵区域。
● A(i:inc1:j,m:inc2:n)：表示访问从第i行至第j行，行间隔为inc1，从第m列至第n列，列间隔为inc2的非相邻的多个矩阵元素。
例2-46：矩阵元素区域的访问示例。
利用randn函数创建一个10×8的0～1正态分布随机矩阵X并进行访问。在命令行窗口中依次输入：
X = randn(10,8)
A = X(2,:)
B = X(3:8,2:6)
得到的结果为：
X =
1.4897 -0.3034 -0.7549 0.6277 0.3714 -0.7423 0.4882 -0.2437
1.4090 0.2939 1.3703 1.0933 -0.2256 -1.0616 -0.1774 0.2157
1.4172 -0.7873 -1.7115 1.1093 1.1174 2.3505 -0.1961 -1.1658
0.6715 0.8884 -0.1022 -0.8637 -1.0891 -0.6156 1.4193 -1.1480
-1.2075 -1.1471 -0.2414 0.0774 0.0326 0.7481 0.2916 0.1049
0.7172 -1.0689 0.3192 -1.2141 0.5525 -0.1924 0.1978 0.7223
1.6302 -0.8095 0.3129 -1.1135 1.1006 0.8886 1.5877 2.5855
0.4889 -2.9443 -0.8649 -0.0068 1.5442 -0.7648 -0.8045 -0.6669
1.0347 1.4384 -0.0301 1.5326 0.0859 -1.4023 0.6966 0.1873
0.7269 0.3252 -0.1649 -0.7697 -1.4916 -1.4224 0.8351 -0.0825
A =
1.4090 0.2939 1.3703 1.0933 -0.2256 -1.0616 -0.1774 0.2157
B =
-0.7873 -1.7115 1.1093 1.1174 2.3505
0.8884 -0.1022 -0.8637 -1.0891 -0.6156
-1.1471 -0.2414 0.0774 0.0326 0.7481
-1.0689 0.3192 -1.2141 0.5525 -0.1924
-0.8095 0.3129 -1.1135 1.1006 0.8886
-2.9443 -0.8649 -0.0068 1.5442 -0.7648
2）线性寻址
线性寻址的原理来自MATLAB将矩阵元素存储在内存空间的存储方法。与矩阵下标寻址相比，线性寻址只需要单一下标即可实现矩阵中任意位置元素的访问。线性寻址的下标是通过矩阵的双下标换算得到的。
一般，设A是一个m×n的矩阵，位于第i行、第j列的元素A(i,j)的单一下标为A((j-1)·m+i)。
例2-47：线性寻址示例。
建立3阶希尔伯特矩阵A，并进行线性寻址访问。在命令行窗口中依次输入：
A = hilb(3)
A(2,3) % 采用矩阵下标寻址的方法访问第2行第3列的元素
A(8)
得到的结果如下：
A =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
ans =
0.2500
ans =
0.2500
3．矩阵元素的赋值
MATLAB使用赋值语句对矩阵元素进行赋值，基本语法如下。
● A(i,j)=value：等号左侧为矩阵中的某个元素；等号右侧为值。
● A=[]：删除矩阵中的所有元素。
例2-48：矩阵元素的赋值示例。
利用magic函数建立一个4阶的魔幻矩阵M，并进行复制操作。在命令行窗口中依次输入：
M = magic(4)
M(2,1) = -2
M(3:4,3:4) = 0
M = []
whos M % 调用whos函数查看矩阵M的详细信息
得到的结果为：
M =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
M =
16 2 3 13
-2 11 10 8
9 7 6 12
4 14 15 1
M =
16 2 3 13
-2 11 10 8
9 7 0 0
4 14 0 0
M =
[]
Name Size Bytes Class Attributes
M 0x0 0 double
4．矩阵元素的扩展与删除
增加或删除矩阵元素最常用的方法是使用赋值语句。
例2-49：对于矩阵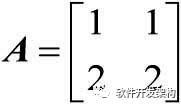
，如果现在要增加一行，则应在命令行窗口中输入：
A = [1 1;2 2]
A(3 , :) = 3 % 整行赋值
A(4,1) = 4;A(4,2) = 5 % 使用单个矩阵元素赋值的方法增加新元素
A(2 , :) = [] % 使用空矩阵[]删除矩阵中的整行或整列
得到的结果为：
A =
1 1
2 2
A =
1 1
2 2
3 3
A =
1 1
2 2
3 3
4 5
A =
1 1
3 3
4 5
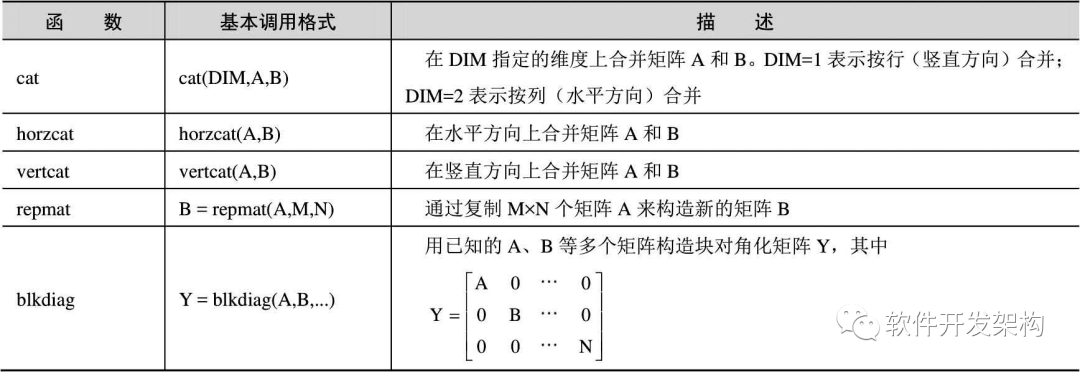
此外，MATLAB提供了多个函数进行矩阵合并操作，从而实现将多个矩阵合并成一个矩阵。这些函数如表2-18所示。
表2-18 矩阵合并函数
例2-50：矩阵合并函数示例。
（1）设有矩阵A= 
、矩阵B= 
、矩阵C=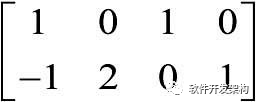 
，利用cat函数分别对矩阵A、B及矩阵A、C进行合并操作，函数中的输入参数DIM分别取DIM=1及DIM=2。
在命令行窗口中首先输入：
A = [2 0 -1;1 3 2];
B = [1 7 -1;4 2 3;2 0 1];
C = [1 0 1 0;-1 2 0 1];
得到矩阵A、B、C。然后使用cat函数对矩阵A、B进行合并操作。
MAB1 = cat(1,A,B) % 将矩阵A、B按行合并
得到结果：
MAB1 =
2 0 -1
1 3 2
1 7 -1
4 2 3
2 0 1
如果合并错误，如：
MAB2 = cat(2,A,B) % 将矩阵A、B按列合并
MAC1 = cat(1,A,C) % 将矩阵A、C按行合并
则得到结果：
错误使用 cat
要串联的数组的维度不一致。
使用cat函数对矩阵A、C进行合并操作，输入如下：
MAC2 = cat(2,A,C) % 将矩阵A、C按列合并
得到结果：
MAC2 =
2 0 -1 1 0 1 0
1 3 2 -1 2 0 1
为了探究矩阵A、B按列合并及矩阵A、C按行合并发生错误的原因，将合并后的矩阵列出来：
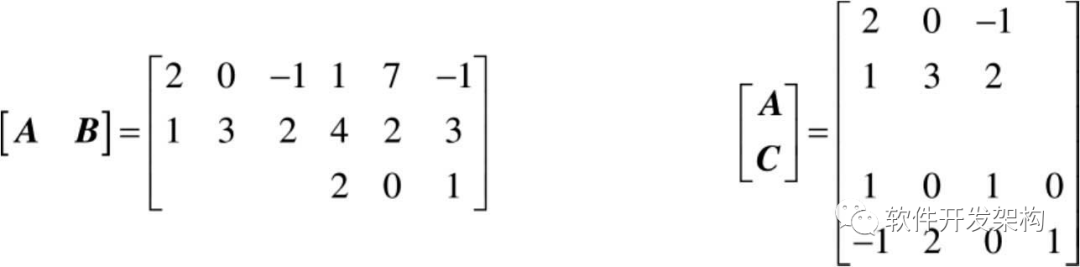
可以看出，由于两个矩阵在某个维度上的长度不一致，从而导致新的矩阵出现残缺。
因此，cat及其相关的函数在将两个矩阵按某个维度进行合并操作时，原始的两个矩阵要在某一个维度上具有相同的长度，否则MATLAB在进行计算时就会发生错误。
（2）使用blkdiag函数构造块对角化矩阵。例如在命令行窗口中输入：
A = [1 1;2 2];B = [3 3;4 4];C = [5 5;6 6];
Y = blkdiag(A,B,C)
得到结果：
Y =
1 1 0 0 0 0
2 2 0 0 0 0
0 0 3 3 0 0
0 0 4 4 0 0
0 0 0 0 5 5
0 0 0 0 6 6
