π day 说 π

一、引言

环境：64位Win 10中文版 + 64位Python 3.6.5

本书配套的电子版图书中的编码和文本处理知识也可以作为理工科教师和科研人员处理文本数据的参考资料之一，毕竟专门开辟章节介绍国家标准《通用规范汉字表》汉字处理的程序设计图书并不多见。

三、π和π day

圆周率是圆的周长与直径的比值，一般用希腊字母 π 表示。π 值是一个无限不循环小数。我国古代数学家祖冲之是世界上第一个将圆周率精确到小数点之后第 7 位数字的人，祖冲之计算的 π 值介于 3.1415926 和 3.1415927 之间。目前，借助计算机，人们可以轻而易举地准确 求出 π 值小数点后面数百万位数字，π 值的前 100 位如下：

π=3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679… 

π 是一个在数学及物理学中普遍存在的数学常数，它的地位非常重要，重要到人类专门因为它建立了一个节日：很多年前，数学界就自发地把 3 月 14 日这一天作为圆周率日来庆祝，俗称 π day。

2019 年 11 月 26 日，联合国教科文组织在第四十届大会上正式宣布 3 月 14 日为“国际数学日”，于是 2020 年 3 月 14 日成为了地球上第一个国际数学日。 今年3月14日，也就是今天，是第四个国际数学日。

>>> import math
>>> math.pi
3.141592653589793

math 标准库的常量 pi 保留到小数点之后 15 位，这个精度足够应付日常计算。如果在某些计算中需要 π 的更多小数位数，可以用一些公式来求得精度更高的 π 值。 

三、莱布尼茨公式 

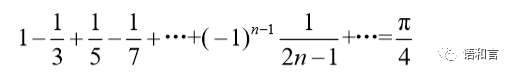
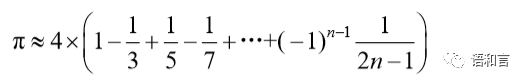
当 n 足够大的时候，π 就能达到一定的精度。 

n = int(input())
pi = 0
sign = 1.0
for i in range(n):
    pi += sign  (2*i+1)
    sign = -sign
pi *= 4
print(f"n={n:9d}，π={pi}")

n=        1，π=4.0
n=       10，π=3.0418396189294032
n=      100，π=3.1315929035585537
n=     1000，π=3.140592653839794
n=    10000，π=3.1414926535900345
n=   100000，π=3.1415826535897198
n=  1000000，π=3.1415916535897743
n= 10000000，π=3.1415925535897915
n=100000000，π=3.141592643589326 

四、韦达公式 

16世纪的法国数学家弗朗索瓦·韦达给出了一个无穷连乘形式的公式： 

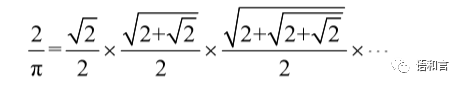
据说该公式是历史上第一个关于圆周率的表达式，它可以变形为：

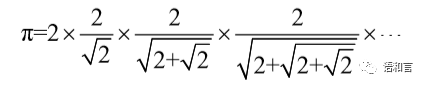
用该公式来计算 π 值，不需要多项就能保证圆周率的小数点后很多位数具有精确值。比如，只需要 13 项就能求出小数点后第 7 位数字的准确值，而莱布尼茨公式需要1亿项才能达到同样的效果。

n = int(input())
pi = 2
t = 0
for i in range(n):
    t = (2+t)**0.5
    pi *= 2/t
print(f"n={n:2d}，π={pi}")

下面是上述代码先后 9 次运行的结果汇总。

n=10，π=3.1415914215112
n=20，π=3.14159265358862
n=30，π=3.1415926535897944
n=40，π=3.1415926535897944
n=50，π=3.1415926535897944
n=60，π=3.1415926535897944
n=70，π=3.1415926535897944
n=80，π=3.1415926535897944
n=90，π=3.1415926535897944

答案是肯定的，当我们想办法保留小数点后很多位小数的时候，我们可以轻松计算到π的小数点后很多位的精确数字。

下面看一下改进后的韦达公式计算π值的程序。

from decimal import Decimal, getcontext
getcontext().prec = 50                 # 设定小数位数为50
for n in range(1, 10):
    n = 10*n
    pi = Decimal("2")
    t = Decimal("0")
    for i in range(n):
        t = (Decimal("2")+t).sqrt()
        pi *= Decimal("2")/t
    print(f"n={n:2d}，π={pi}")

n=10，π=3.1415914215111999739979717637408339557475626500859
n=20，π=3.1415926535886182366142085907724078849809629024672
n=30，π=3.1415926535897932373420742986972462357901345802523
n=40，π=3.1415926535897932384626423146215471592362237674489
n=50，π=3.1415926535897932384626433832784837325517712966676
n=60，π=3.1415926535897932384626433832795028832252306506379
n=70，π=3.1415926535897932384626433832795028841971684724656
n=80，π=3.1415926535897932384626433832795028841971693993788
n=90，π=3.1415926535897932384626433832795028841971693993797

通过将上述结果和圆周率前 100 位小数比对，我们发现，当 n=90 的时候，小数点后前 47 位数字都已经是准确的了。这说明用韦达公式来求圆周率是可行的，前面的程序的几次运行结果在 n=40 之后不再变动，果然是由于浮点数精度误差引起的。

上述程序用到了decimal 标准库的 Decimal 类，关于 Decimal类的用法，请参考胡凤国老师的图书《Python程3序设计（基于计算思维和新文科建设）》的第 12.3 节，本篇文章节也是节选该书。感兴趣的小盆友可以去阅读相应的章节。

五、讨论

1、我们可以在改进后的韦达公式计算π值程序的基础上再修改一下，让它能计算出π值的小数点后100位精确值，小盆友们觉得应该更改哪些地方呢？

2、经过实际测算，改进后的韦达公式计算π值程序可以在计算170 项连乘积之后计算出π值的小数点后100位精确值。这还不是最快最好的公式。最快最好的公式是拉马努金公式，它只需要计算公式前面很少的项数就能将计算结果精确到π的小数点后100位。关于这个公式，以后有机会的话再给小盆友们分享。

六、联系交流

七、图书目录

图书《Python程序设计（基于计算思维和新文科建设）》目录如下（手机端可以用手指上下滑动下面灰色区域的文字来查看全部目录，电脑端可以用鼠标滚动滚轮或拖动下面文本框右边的滚动条来浏览全部目录）：