学会算法，帮你轻松求解公务员考试题

一、引言

环境：64位Win 10中文版 + 64位Python 3.7.6

本书配套的电子版图书中的编码和文本处理知识也可以作为理工科教师和科研人员处理文本数据的参考资料之一，毕竟专门开辟章节介绍国家标准《通用规范汉字表》汉字处理的程序设计图书并不多见。

三、解法一：暴力枚举

思路：枚举1、2、……、12的所有的排列，然后统计合法的排列总数。程序如下：

上述题目的输出是 232 ，所以，那道公考行测题选 C  。

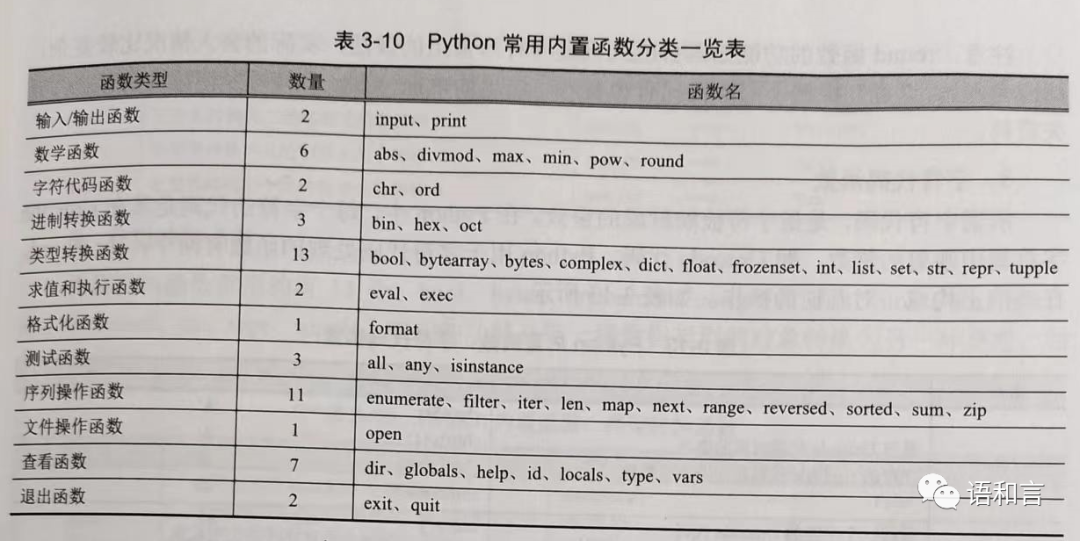
上面的程序中，用了几个内置函数：abs、all、enumerate、range，还用了一个来自标准库 itertools 的排列函数 permutations。

关于这些函数的用法，新书《Python程序设计（基于计算思维和新文科建设）》当中都有介绍，感兴趣的同学请参考书中相应的章节。

本号曾专门写文章介绍过内置函数all和它的兄弟any，感兴趣的读者朋友可以参考一下：

《Python内置函数介绍：all和any》

这种暴力解法虽然能求解，但它的缺点就是慢，上面的程序需要10分多钟才能运行出来。我们加上时间库，来看看究竟能耗费多长时间：

上述程序某一次的运行结果如下：

我们发现12个人的情况下，程序需要运行612秒才能出结果。

考场上不可能让我拿个电脑去敲程序吧，即使让带，十分钟的时间谁能耗得起？这个程序对考公务员没有任何帮助呀？是的，没有任何帮助，如果我们学会了算法，那就不一样了。且看下面的分析。

四、解法二：分治法

思路：假设有k个人参加排列，则原始排列1、2、3、……、k-1、k。按题意，新的排列需要交换原始排列中相邻两数的位置，问有多少种不同的交换结果。

显然：

只把第1和第2交换一下，其他不变，是一种交换结果；

只把第2和第3交换一下，其他不变，是一种交换结果；

把第1和第2交换、3和4交换，其他不变，是一种交换结果；

……

如果把原始序列也当成一种交换方法（相邻的两数之间进行零次交换）的话，事情就简单了：

令g(k)表示交换方法总数，考虑第k个人：

（1）参与交换，只能跟第k-1交换，前面k个人交换的结果是g(k-2)

（2）不参与交换，则前面k-1个人交换的结果是g(k-1)

g(k)=g(k-1)+g(k-2)，k>2

g(k)=k，k=1、2

这不就是兔子数列的推导式嘛，除了第一项和第二项跟兔子数列不一样之外，推导式是完全一样的。

所以，接下来不用编程，也会知道g(k)的前12项结果：

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233

因此，g(12)=233,再减去一个原始排序结果，不就是232嘛。这种思考问题的方法，是算法里面的分治法。

新书《Python程序设计（基于计算思维和新文科建设）》当中在介绍递归函数的时候提到过三种算法：减治法、分治法和动态规划法，感兴趣的读者朋友可以去阅读书中的相关章节。

这道公务员行测题恰好就是用分治法来轻松求解。看，学会算法是不是有助于考公务员呢？

下面给出这道题目的分治法思路的程序解法：

五、讨论

中国传媒大学李国政同学提供了另一个巧妙的思路。这里直接上程序：

感兴趣的读者朋友可以探究一下这个程序背后的算法思想 。

七、图书目录

图书《Python程序设计（基于计算思维和新文科建设）》目录如下（手机端可以用手指上下滑动下面灰色区域的文字来查看全部目录，电脑端可以用鼠标滚动滚轮或拖动下面文本框右边的滚动条来浏览全部目录）：