中心极限定理
中心极限定理
中心极限定理指出大量随机变量近似服从正态分布的条件，是概率论中最重要的一类定理，实际应用广泛。
独立同分布的中心极限定理 设随机变量X1,X2,…相互独立，服从同一分布，且具有数学期望和方差：E(Xk)=μ,D(Xk)=σ2>0(k=1,2,…)，则随机变量之和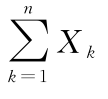
的标准化变量
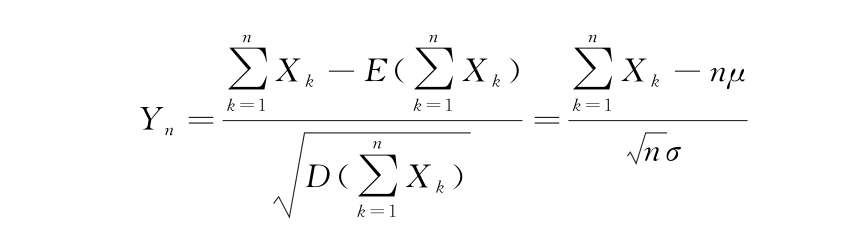
的分布函数Fn(x),对于任意的x满足：
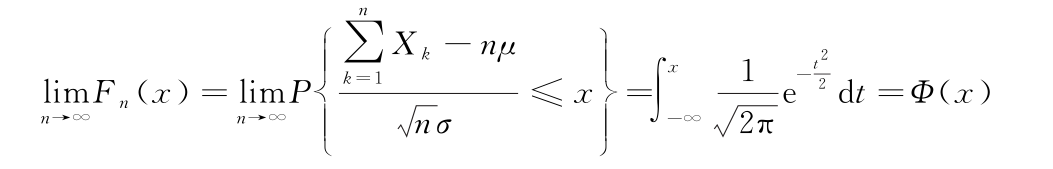
上述定理表明，均值为μ，方差为σ2>0的独立同分布随机变量序列X1,X2,…,Xn之和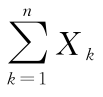
的标准化变量，当n充分大时，有：
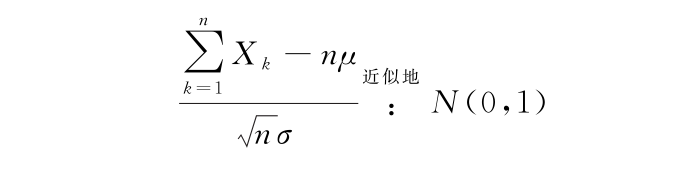
取随机变量序列独立且服从均匀分布U(5，15)，检验上述定理，代码如下：
运行结果如图17.3所示。
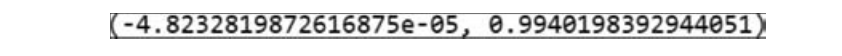
■ 图17.3
从输出结果可以看到，Y近似服从标准正态分布。
棣莫弗-拉普拉斯(De Moivre-Laplace)定理 设随机变量ηn（n=1,2,…）服从参数为n,p(0<p<1)的二项分布，则对于任意x，有：
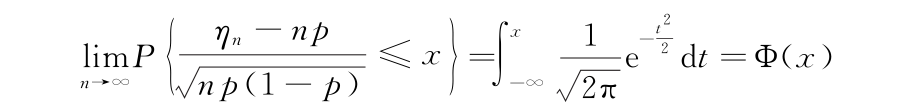
取随机变量服从参数为n=10000，p=0.3的二项分布，检验代码如下：
运行结果如图17.4所示。
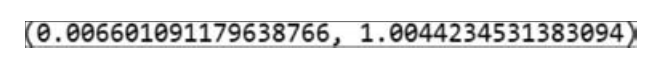
■ 图17.4
可以看到Y近似服从标准正态分布。
De Moivre-Laplace定理表明正态分布是二项分布的极限分布，当n充分大时，可以用正态分布来计算二项分布的概率。
参考书籍
《Python漫游数学王国——高等数学、线性代数、数理统计及运筹学》
ISBN：9787302597797
作者：毕文斌、毛悦悦
定价：128元
内容简介
本书参考高等学校理工科“高等数学”“线性代数”“概率论与数理统计”“运筹学”等课程教学大纲，使用Python语言实现相关计算、图形展示及模型求解，内容包含Python编程语言入门、极限的运算、函数的求导及积分、微分方程求解、级数、行列式计算、线性方程组求解、随机变量及其分布、随机变量的数字特征、参数估计、假设检验、方差分析与回归、线性规划、非线性规划、动态规划、图与网络计划及排队论等。本书内容翔实，文字精练，例题丰富，注重本科数学理论与科学计算的密切结合。本书可以作为高等学校理工科在校本科生的学习实验用书，也可以作为对Python科学计算感兴趣的人员的参考用书。
