
对于杂乱无章的数据,数据的整理与描述显得尤为重要。本文通过例子介绍频数分布表、直方图,以及箱线图的绘制。
直方图和箱线图
对于杂乱无章的数据,数据的整理与描述显得尤为重要。本节通过例子介绍频数分布表、直方图,以及箱线图的绘制。
【例18.1】下面列出了84个伊特拉斯坎(Etruscan)人男子的头颅的最大宽度(mm),试画出这些数据的“频率直方图”。

解 这些数据杂乱无章,先对它们进行整理。首先引入numpy与pandas,代码如下:

统计数据的最小值与最大值,代码如下:

运行结果如图18.28所示。

■ 图18.28
可以看到,所有的数据落在区间[126,158]上,现取区间[124.5,159.5],将其等分为7个小区间,代码如下:

运行结果如图18.29所示。
 ■ 图18.29
■ 图18.29
统计落在每个区间的数据频数,代码如下:

运行结果如图18.30所示。

■ 图18.30
注释/
cut()函数用于将数据进行离散化,即将连续的变量放入离散区间。cut(x, bins,right: bool = True, labels=None, retbins: bool = False,precision: int = 3, include_lowest: bool = False, duplicates: str = 'raise')中参数x是待离散化的一维数组;bins可以是整数,表示将x的范围划分为多少个等距的区间,也可以是一个序列,表示划分的区间端点;right表示是否包含右端点,默认为True;labels表示是否用标签代替返回的区间;precision表示区间端点值的精度;include_lowest表示第一个区间是否包含左端点。
接下来,计算每组的频率以及累计频率,每组频率代码如下:

运行结果如图18.31所示。

■ 图18.31
计算累积频率,代码如下:

运行结果如图18.32所示。
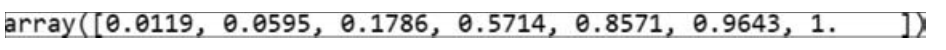
■ 图18.32
注释/
(1) Series的values属性可获取其值的数组表示形式。
(2) cumsum()用于求累积和。
绘制频数分布表,代码如下:

运行结果如图18.33所示。
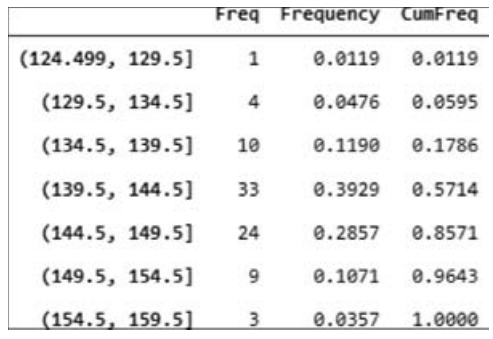
■ 图18.33
最后,用矩形的面积表示频率,绘制频率直方图,代码如下:

运行结果如图18.34所示。
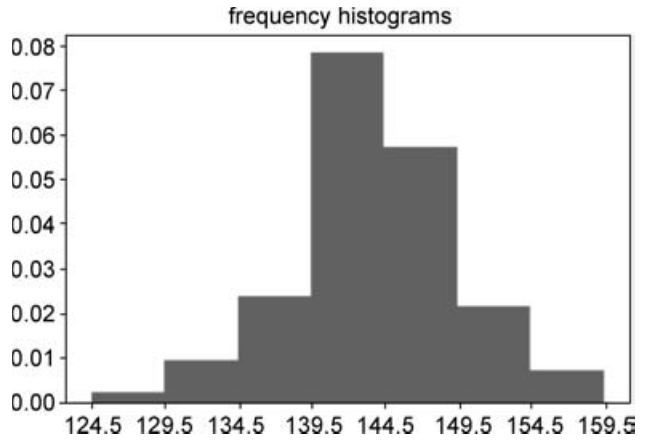
■ 图18.34
也可以同时给出数据的核密度估计曲线,代码如下:

运行结果如图18.35所示。
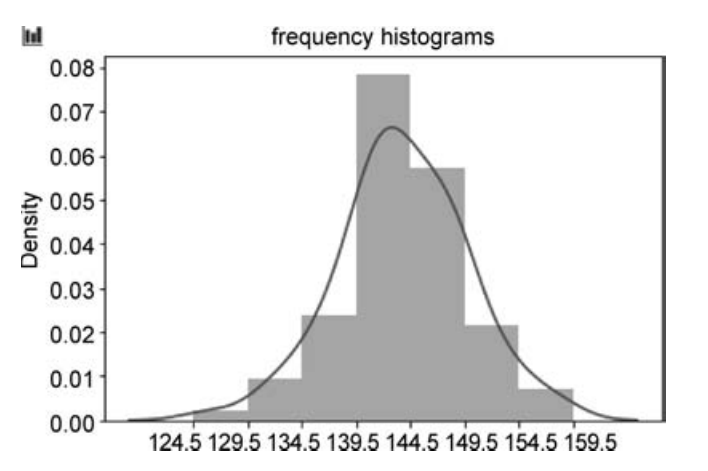
■ 图18.35
或者拟合正态分布,给出估计的概率密度函数,代码如下:

运行结果如图18.36所示。
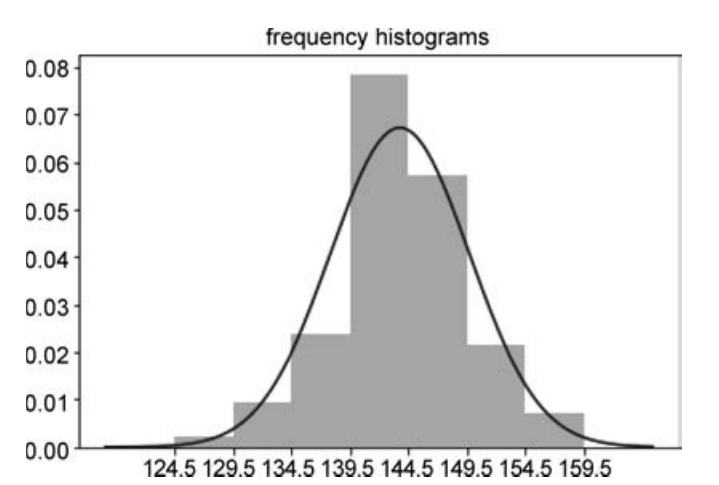
■ 图18.36
注释/
(1) seaborn是基于matplotlib的数据可视化库。它提供了一个高度交互式界面,用于绘制有吸引力和信息丰富的统计图形。
(2) distplot()集合了matplotlib的hist()与seaborn的kdeplot()以及rugplot()。它也可利用scipy库的fit拟合分布,并给出估计的概率密度函数。更多distplot的用法可在jupyter单元格中输入“sns.distplot?”查看。
【例18.2】设一组容量为18的样本值如下(已经过排序):
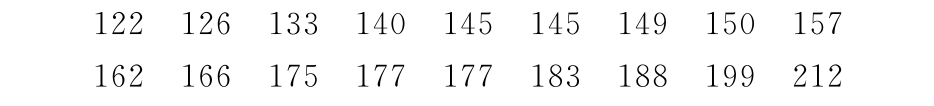
求样本分位数:x0.2,x0.25,x0.5。
解求百分位数可使用numpy中的percentile(),也可使用pandas中的quantile()。
使用percentile()求分位数,代码如下:

运行结果如图18.37所示。
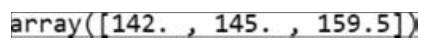
■ 图18.37
注释/
np.percentile(X,q=[20,25,50])中q指要计算的百分位数或百分位数序列,必须介于0和100(含0和100)。
再来看使用quantile()求分位数,代码如下:

运行结果如图18.38所示。

■ 图18.38
注释/
(1) quantile()中分位数的表示形式与percentile()不同。
(2) 不同的软件计算的分位数值可能会有出入,原因是计算分位数值时所采取的算法不同。上述两种方法可通过调整参数interpolation,选取不同的插值方法,默认为线性“linear”,还可选取“lower”“higher”“midpoint”“nearest”来实现。
【例18.3】以下是已经过排序的8个病人的血压(mmHg)数据,试画出箱线图。
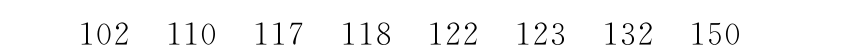
解 代码如下:

运行结果如图18.39所示。
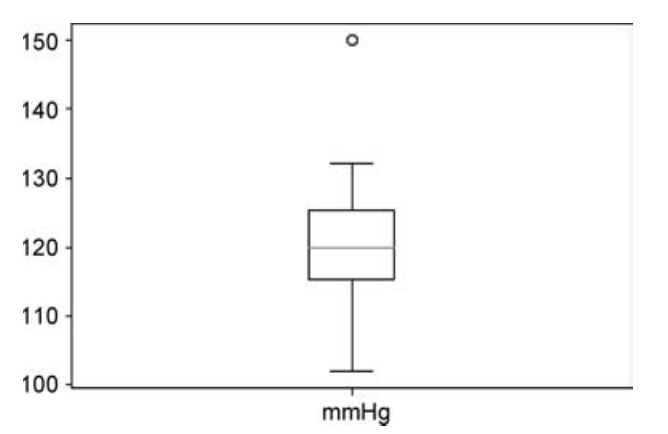
■ 图18.39
注释/
(1) boxplot()用于绘制箱线图,它由五个数值点组成:最小值,下四分位数,中位数,上四分位数,最大值。下四分位数、中位数、上四分位数组成一个“带有隔间的盒子”,也可以往盒子里面加入平均值。箱子两侧的延伸线称为“胡须”,揭示数据的范围,“胡须”外部的点称为离群点。
(2) boxplot()参数众多,这里截取一部分来看:plt.boxplot(x,notch=None,sym=None,vert=None,whis=None,positions=None,widths=None,patch_artist=None,meanline=None,showmeans=None,showcaps=None,showbox=None,showfliers=None,labels=None,)中参数x指定要绘制箱线图的数据,可以是一个数组,或一个数组序列;notch表示是否取凹口的形式展现箱线图,默认非凹口;sym用于指定异常点的形状;vert表示是否将箱线图垂直摆放,默认为垂直摆放;whis指定上下须与上下四分位的距离,默认为1.5倍的四分位间距;positions指定箱线图的位置,默认为[0,1,2,…];widths指定箱线图的宽度;patch_artist表示是否填充箱体的颜色;meanline表示是否用线的形式表示均值,默认用点来表示;showmeans表示是否显示均值,默认不显示;showcaps表示是否显示箱线图顶端和末端的两条线,默认显示;showbox表示是否显示箱线图的箱体,默认显示;showfliers表示是否显示离群值,默认显示;labels为箱线图添加标签,类似于图例的作用。
【例18.4】下面给出了25个男子和25个女子的肺活量(已排序)。

试分别画出这两组数据的箱线图。
解 代码如下:

运行结果如图18.40所示。

■ 图18.40
注释/
箱线图特别适用于比较两个或两个以上数据集的性质,因此,常将几个数据集的箱线图画在同一个数轴上。此时只需将参数x设置成数组序列即可,每一个数组表示一个数据集。
参考书籍

《Python漫游数学王国——高等数学、线性代数、数理统计及运筹学》
ISBN:9787302597797
作者:毕文斌、毛悦悦
定价:128元

内容简介
本书参考高等学校理工科“高等数学”“线性代数”“概率论与数理统计”“运筹学”等课程教学大纲,使用Python语言实现相关计算、图形展示及模型求解,内容包含Python编程语言入门、极限的运算、函数的求导及积分、微分方程求解、级数、行列式计算、线性方程组求解、随机变量及其分布、随机变量的数字特征、参数估计、假设检验、方差分析与回归、线性规划、非线性规划、动态规划、图与网络计划及排队论等。本书内容翔实,文字精练,例题丰富,注重本科数学理论与科学计算的密切结合。本书可以作为高等学校理工科在校本科生的学习实验用书,也可以作为对Python科学计算感兴趣的人员的参考用书。













