算法竞赛系列 | 莫比乌斯函数和莫比乌斯反演

本文简单介绍莫比乌斯函数。这个数学概念十分抽象，读者可能困惑莫比乌斯函数是怎么来的，本节将解答这个问题。

1. 莫比乌斯函数的定义和性质

莫比乌斯函数以数学家Möbius的名字命名。莫比乌斯函数是狄利克雷卷积的重要工具，它也是数论和组合数学的重要的积性函数。

莫比乌斯函数μ(n)定义为，其中P_i为不同的素数

举一些例子：μ(1)=1，μ(2)=-1，μ(3)=-1，μ(4)=μ(2²)=0，μ(5)=-1，μ(6)=μ(2×3)=1，μ(7)=-1，μ(8)=μ(2³)=0，μ(330)=μ(2×3×5×11)=(-1)⁴=1，μ(660)=μ(2²×3×5×11)=0。

莫比乌斯函数μ(n)是积性函数。它有一个与欧拉函数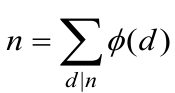类似的定理。

定理6.16.1莫比乌斯函数的和函数在整数n处的值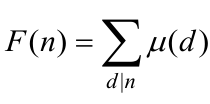，满足

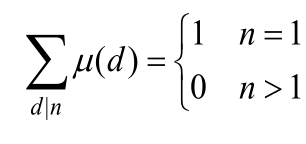
证明

(1) n=1时，显然有。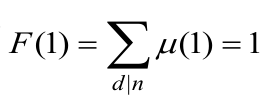

(2) n>1时，根据积性函数的定义，有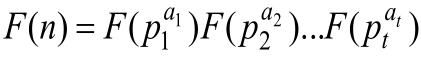，其中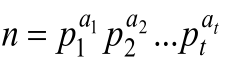是质因数分解。如果能证明F(p^k)=0，即有F(n)=0。因为当i≥2时，μ(pⁱ)=0，有

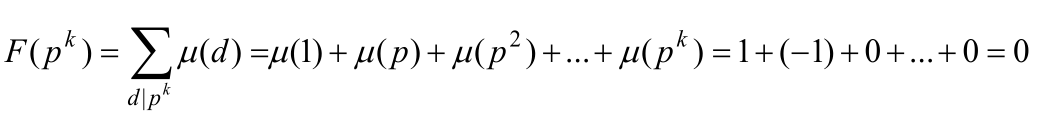
下面给出莫比乌斯函数线性筛代码，求1～n内的莫比乌斯函数，与欧拉函数线性筛的代码几乎一样，此处不做解释。

2.  莫比乌斯函数的由来

看到莫比乌斯函数的定义，读者可能感到奇怪,它是怎么来的？有什么用？

下面的内容引用自《初等数论及其应用》第199页，解释了莫比乌斯函数的来龙去脉。

设f为算术函数，f的和函数F的值为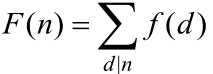，显然，F由f的值决定。这种关系可以反过来吗？也就是说，是否存在一种用F求出f的值的简便方法？本节给出这样的公式，看什么样的公式可行。

若f是算术函数，F是它的和函数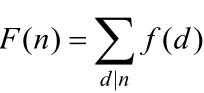，按定义展开F(n)，n=1，2，…，8，有

F(1)=f(1)

F(2)=f(1)+f(2)

F(3)=f(1)+f(3)

F(4)=f(1)+f(2)+f(4)

F(5)=f(1)+f(5)

F(6)=f(1)+f(2)+f(3)+f(6)

F(7)=f(1)+f(7)

F(8)=f(1)+f(2)+f(4)+f(8)

根据上述方程，可以解得

f(1)=F(1)

f(2)=F(2)-F(1)

f(3)=F(3)-F(1)

f(4)=F(4)-F(2)

f(5)=F(5)-F(1)

f(6)=F(6)-F(3)-F(2)+F(1)

f(7)=F(7)-F(1)

f(8)=F(8)-F(4)

注意f(n)等于形式为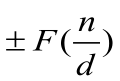的一些项之和，其中d|n。从这一结果中，可能有这样一个等式，形式为

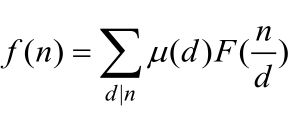
其中，μ为算术函数。如果等式成立，计算得到μ(1)=1，μ(2)=-1，μ(3)=-1，μ(4)=0，μ(5)=-1，μ(6)=1，μ(7)=-1，μ(8)=0(读者已经发现和前面莫比乌斯函数的值一样)。

又因为F(p)=f(1)+f(p)，得f(p)=F(p)-F(1)，其中p是素数，则μ(p)=-1。

又因为F(p²)=f(1)+f(p)+f(p²)，有f(p2)=F(p²)-(F(p)-F(1))-F(1)=F(p²)-F(p)。

这要求对任意素数p，有μ(p²)=0。类似地，推理得出对任意素数p及整数k>1，有μ(p^k)=0。如果猜想μ是积性函数，则μ的值就由质数幂处的值决定。

3. 莫比乌斯反演

定理6.16.2莫比乌斯反演(Möbius Inversion)公式。若f是算术函数，F为f的和函数，对任意正整数n，满足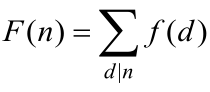，则有。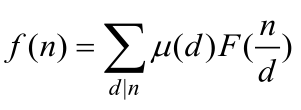

从定理6.16.2可以推出定理6.16.3。

定理6.16.3设f是算术函数，它的和函数为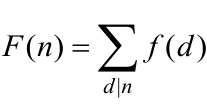。如果F是积性函数，则f也是积性函数。

莫比乌斯反演不需要f是积性函数。运用莫比乌斯反演可以将一些函数转化，从而降低计算难度。