计算几何的基础是点积和叉积，它们定义了向量的大小和方向的关系，是其他计算几何概念和算法的出发点。在点积和叉积的基础上，本篇介绍两道复杂的例题说明三维几何模板代码的使用。
化球为圆
● 例8.9Ghost busters(poj 2177)
问题描述：在立体空间的第1象限内(x，y，z≥0)有很多球，这些球可能互相包含、重合。从原点(0，0，0)发出一条射线，问最多能穿过多少球？穿过球的边界也算。
输入：第1行输入整数N，表示球的数量，0≤N≤100。后面N行中，每行描述一个球，输入4个整数xi、yi、zi、ri，表示第i个球的球心坐标和半径，1≤ri≤min(xi、yi、zi)。
输出：第1行输出能穿过的球的最多个数； 第2行输出这些球的号码，按从小到大顺序输出。
从原点出发的射线太多，不可能一一检查，需要缩小检查范围。应该检查哪些射线？显然，那些经过球体交点的射线能穿过更多的球体。为了简化求交点，用“化球为圆”的技巧： 从原点(0，0，0)看去，这些球都是圆圈，这样就把穿过球体的问题变成了穿过圆圈的问题。
本题的求解步骤： ①求出所有圆圈的交点； ②对每个交点，与原点连成一条射线，暴力统计这条射线能穿过多少球体； ③对最佳射线，求它穿过的球体。
(1) 求任意两个球的交点。
任选两个球，从原点看过去，这两个球变成两个圆圈。这两个圆圈是否相交？为了判断它们的关系，把它们的圆心调整到与原点等距的位置，它们的半径做等比缩放。如图8.24所示，保持球1不变，调整球2，把球心c2与原点的距离调整到与球心c1相等的位置。根据三角形的比例关系，此时球2的新球心位置是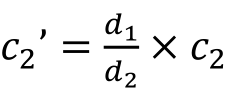
，注意c2是三维坐标点； 新半径为
。
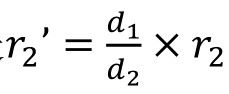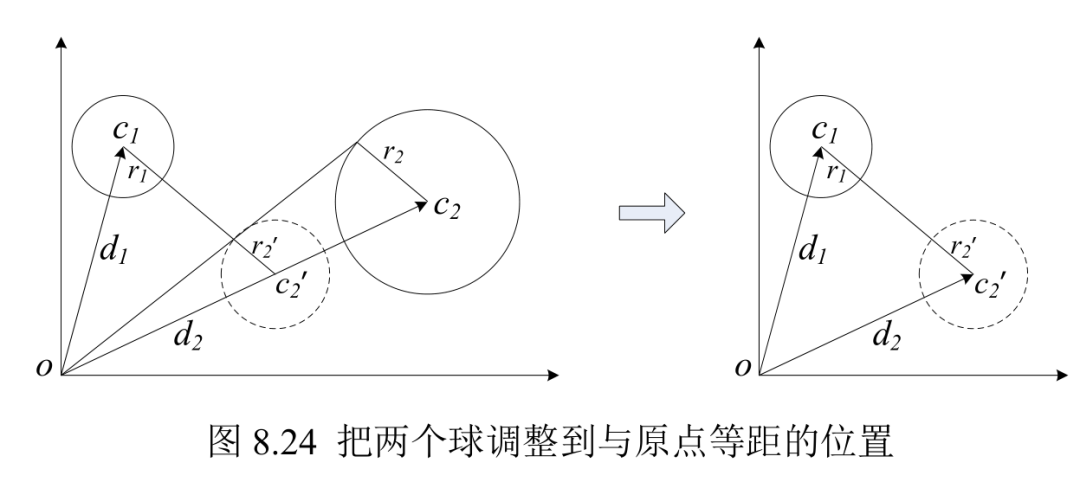
两个圆的关系有4种： 相切、相离、包含、相交。相切时，有一个交点； 相交时，有两个交点，图8.25是相交的情况，交点是v和它的对称点。后面代码中的intersect()函数求任意两个圆圈的交点，存储到vectorP中。请对照图8.25分析函数的代码。
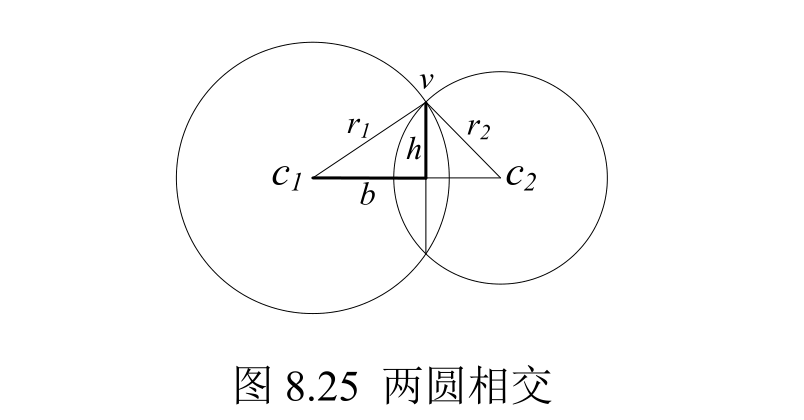
(2) 计算射线能穿过的最多球体数量。得到交点后，连接原点与每个交点产生射线，统计每条射线能经过的球体数量，记录最大数量并输出。详见代码第75~80行。
(3) 计算这条最佳射线穿过的球体。详见代码第81~85行。
#include <cmath>#include <vector>#include <algorithm>using namespace std;const int N=105;const double eps = 1e-7;int sgn(double x){ //判断x是否等于0if(fabs(x)<eps) return 0;else return x<0?-1:1;}struct Point3{double x,y,z;Point3(){}Point3(double x,double y,double z):x(x),y(y),z(z){}Point3 operator + (Point3 B){return Point3(x+B.x,y+B.y,z+B.z);}Point3 operator - (Point3 B){return Point3(x-B.x,y-B.y,z-B.z);}Point3 operator * (double k){return Point3(x*k,y*k,z*k);}Point3 operator (double k){return Point3(x/k,y/k,z/k);}Point3 adjust (double L){ //调整长度double len=sqrt(x*x+y*y+z*z);L/=len;return Point3(x*L,y*L,z*L);}};typedef Point3 Vector3;double Dot(Vector3 A,Vector3 B){return A.x*B.x+A.y*B.y+A.z*B.z;} //点积Vector3 Cross(Vector3 A,Vector3 B){ return Point3(A.y*B.z-A.z*B.y,A.z*B.x-A.x*B.z,A.x*B.y-A.y*B.x);} //叉积double Len(Vector3 A){return sqrt(Dot(A,A));} //向量的长度double Distance(Point3 A,Point3 B) //两点的距离{ return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y)+(A.z-B.z)*(A.z-B.z)); }struct Line3{ //三维：线Point3 p1,p2;Line3(){}Line3(Point3 p1,Point3 p2):p1(p1),p2(p2){}};double Dis_point_line(Point3 p, Line3 v) //三维：点到直线距离{ return Len(Cross(v.p2-v.p1,p-v.p1))/Distance(v.p1,v.p2); }vector<Point3> P; //储存球的交点void intersect(Point3 c1,double r1,Point3 c2,double r2){ //计算球的交点double d1=Len(c1),d2=Len(c2); //球心到原点距离c2=c2/d2*d1; //调整球2，让两个球心与原点等距r2=r2/d2*d1;double d=Len(c1-c2); //连心线长度if(sgn(d-r1-r2)==0){P.push_back(c1+(c2-c1)/d*r1);return;} //(1)相切，存相切的点if(sgn(d-r1-r2)>0) return; //(2)相离，没有交点if(sgn(d-fabs(r1-r2))<=0) return; //(3)包含，没有交点//(4)下面处理两个圆相交，有两个交点double b=(r1*r1+d*d-r2*r2)/(2*d); //余弦定理double h =sqrt(r1*r1-b*b);Point3 M=c1+(c2-c1)/d*b; //两交点中点所在位置Point3 v=Cross(c1,M); //叉积求得两交点所在直线的向量v=v.adjust(h)+M;P.push_back(v);P.push_back(M*2-v);}int check(Point3 p,Point3 c,double r){ //检查交点p是否在球内或球面上Line3 v(Point3(0,0,0),p);double x = Dis_point_line(c,v);return sgn(x-r) <= 0;}Point3 c[N]; //球心double r[N]; //球半径int main (){int n; scanf("%d",&n);for(int i=1;i<=n;i++) {scanf("%lf%lf%lf",&(c[i].x),&(c[i].y),&(c[i].z));scanf("%lf",&r[i]);P.push_back(c[i]);}for(int i=1;i<=n;i++) //求任意两个球的交点，记录在vector P中for(int j=i+1;j<=n;j++)intersect(c[i],r[i],c[j],r[j]);int ans=0,temp,w; //w记录选中的交点for(int i=0;i<P.size();i++) { //检查每条射线，记录穿过最多球体的数量temp=0;for(int j=1;j<=n;j++) temp += check(P[i],c[j],r[j]);if(temp>ans) ans=temp, w=i;}printf("%d\n",ans);for(int i=1;i<=n && ans;i++) //枚举所有球，判断与选定的最佳射线是否相交if(check(P[w],c[i],r[i])) {ans--;printf(ans!=0?"%d ":"%d\n",i);}return 0;}
仿射变换
● 例8.10A letter to programmers
https://vjudge.net/problem/UVALive-5719
问题描述： 在立体空间中对坐标点做以下操作。
translate tx ty tz： 平移，把点(x，y，z)移动到(x+tx，y+ty，z+tz)。
scale a b c： 缩放，把点(x，y，z) 移动到(ax，by，cz)。
rotate a b c d： 旋转，旋转轴是从(0，0，0)到(a，b，c)的直线，旋转角度为d。如果站在(a，b，c)看向(0，0，0)，会看见旋转是逆时针的。
repeat k： 重复k次，整数k是一个32位的非负整数。
end： repeat指令的结束指令。若前面没有repeat，则表示整个结束。
输入： 每个测试第1行输入整数n，表示给定点的数量，然后有不多于100行指令，每行代表一个指令。指令后有n行，每行输入一个坐标点。除了n和k，其他数字都是不大于1000的浮点数。最后以0结尾。
输出： 对每个测试，打印n行，每行输出3个浮点数，表示点的新位置。保留两位小数。在每两个测试之间打印一个空行。
本题是三维平移、缩放、旋转，是一道模拟“仿射变换”的题目。由于重复次数k非常大，需要使用矩阵快速幂。
本题的求解过程直接模拟题目的要求即可，不需要更多解释，细节见下面的代码。
//改写自：www.cppblog.com/hanfei19910905/archive/2012/06/24/180035.html#include<bits/stdc++.h>using namespace std;const double eps = 1e-6;const double pi = acos(-1.0); //圆周率，精确到15位小数：3.141592653589793const int N = 4;struct matrix {double num[N][N];matrix (double a){ //单位矩阵乘以amemset(num,0,sizeof(num));for(int i=0;i<N;i++) num[i][i] = a;}matrix(double x,double y,double z){ //平移变换memset(num,0,sizeof(num));for(int i=0;i<N;i++) num[i][i] = 1; //单位矩阵num[3][0] = x; num[3][1] = y; num[3][2] = z;}matrix(double x,double y,double z, int X){ //缩放变换memset(num,0,sizeof(num));for(int i=0;i<N;i++) num[i][i] = 1; //单位矩阵num[0][0] = x; num[1][1] = y; num[2][2] = z;}matrix(double P[3],double ang){ //旋转变换memset(num,0,sizeof(num));for(int i=0;i<N;i++) num[i][i] = 1; //单位矩阵double flag [3][3] = {0,1,-1, -1,0,1, 1,-1,0};double sum = P[0] + P[1] + P[2];for(int i=0;i<3;i++)for(int j=0;j<3;j++)if(i==j) num[i][j] = P[i]*P[i] + (1-P[i]*P[i]) * cos(ang);else num[i][j] = P[i]*P[j]*(1-cos(ang))+(sum-P[i]-P[j])*sin(ang)*flag[i][j];}};matrix operator * (const matrix& a, const matrix& b){ //普通矩阵乘法。注意constmatrix c(0);for(int i=0; i<N; i++)for(int j=0; j<N; j++)for(int k = 0; k<N; k++)c.num[i][j] += a.num[i][k] * b.num[k][j];return c;}matrix pow_matrix(matrix a, int n){ //普通矩阵快速幂matrix ans(1);while(n) {if(n&1) ans = ans * a;a = a * a;n>>=1;}return ans;}matrix dfs(){matrix ans(1);while(1){string cmd; cin >> cmd;if(cmd=="end") return ans;if(cmd=="repeat"){int k; scanf("%d",&k);matrix temp = dfs();ans = ans * pow_matrix(temp, k);}else {double x,y,z; scanf("%lf%lf%lf",&x,&y,&z);if(cmd == "translate") {matrix temp(x,y,z); ans=ans*temp;}else if(cmd == "scale"){matrix temp(x,y,z,0); ans=ans*temp;}else if(cmd == "rotate"){double a; scanf("%lf",&a);a = a/180*pi;double sum = sqrt(x*x + y*y +z*z);double p[3] = {x/sum, y/sum, z/sum};matrix temp(p,a);ans = ans * temp;}}}}int main(){int n;while(~scanf("%d",&n) && n){matrix t = dfs();while(n--){double x,y,z,px,py,pz; scanf("%lf%lf%lf",&x,&y,&z);px = x*t.num[0][0] + y*t.num[1][0] + z*t.num[2][0] + t.num[3][0];py = x*t.num[0][1] + y*t.num[1][1] + z*t.num[2][1] + t.num[3][1];pz = x*t.num[0][2] + y*t.num[1][2] + z*t.num[2][2] + t.num[3][2];printf("%.2f %.2f %.2f\n",px+eps,py+eps,pz+eps);}puts("");}}
《算法竞赛》系列推文正在连载中，欢迎持续关注！
扫码优惠购书
