
组合数学是研究离散结构的存在、计数、分析、优化等问题的一门学科。本篇主要介绍基本概念:加法原理、乘法原理、排列与组合的常用公式。
基本概念
1. 加法原理和乘法原理
有4个基本的计数原理:加法原理、乘法原理、除法原理、减法原理。下面介绍加法原理和乘法原理。
(1) 加法原理: 设集合S划分为S1,S2,…,Sm,则S的元素个数可以通过找出它的每部分元素的个数来确定,即|S|=|S1|+S2|+…+|Sm|。通俗地说,一件事可以用m类不同的方法完成,其中第i类有ai种不同的方法,则总方法数为a1+a2+…+am。加法原理是全体等于部分和的公式化描述。在加法原理中,如果集合S1,S2,…,Sm可以重叠,就是容斥原理。
(2) 乘法原理: 令S是元素的序偶(a,b)的集合,其中第1个元素a来自大小为p的一个集合,而对于a的每个选择,元素b有q种选择,则S的大小为p×q。乘法原理是加法原理的推论,因为整数的乘法就是重复的加法。例如,从8男7女5儿童中选出一男一女一儿童的方法有8×7×5=280种。
2. 排列
排列是有序的,把n个元素的集合S的一个r排列理解为n个元素中的r个元素的有序摆放。
(1) 不可重复排列数: 从n个不同的物品中不重复地取出r个,排列数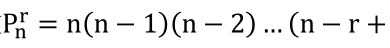
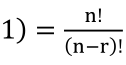 。
。
(2) 可重复排列数: 从n个不同的物品中可重复地取出r个,排列数为nr。
例如,对26个字母排序,要求5个元音字母中的任意两个不能连续出现,问有多少种排序方法?
首先对21个辅音字母排序,有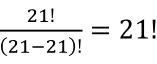 种(0!=1);然后把元音字母插到这21个辅音字母之间,有22个位置可以插,等价于从22个物品中取出5个,有
种(0!=1);然后把元音字母插到这21个辅音字母之间,有22个位置可以插,等价于从22个物品中取出5个,有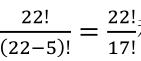 种方法。最后根据乘法原理,把两个步骤相乘,得出有
种方法。最后根据乘法原理,把两个步骤相乘,得出有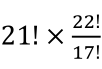 种方法。
种方法。
上面的排列是线性的,所有元素排成一条线。如果不是排成一条线,而是一个圆,由于产生了循环,那么排列的数量要减少。如果把这个圆排列拆成线性排列,可以从任意位置拆开。
(3) 圆排列(循环排列、环排列)的排列数:从n个元素中选r个的圆排列的排列数为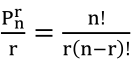 。
。
3. 组合
排列是有序的,组合是无序的,把n个元素的集合S的r组合理解为从S的n个元素中对r个元素的无序选择,即r是S的一个子集。
如果S中的元素都不相同,组合数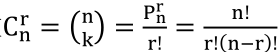 。注意这里的符号,组合数的表示有两种常用符号:
。注意这里的符号,组合数的表示有两种常用符号: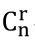 、
、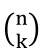 ,其中Crn的n在下面,
,其中Crn的n在下面,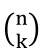 的n在上面。
的n在上面。
例如,平面上的20个点,没有3个点共线。问这些点能确定多少条直线?能确定多少个三角形?
任意两点确定一条直线,即n=20,r=2,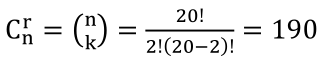 ;任意3点确定一个三角形,
;任意3点确定一个三角形,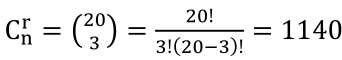 。
。
组合数有3个重要性质。
(1) Crn=Cn-rn。从n个元素中拿出r个,等价于从n个元素中丢掉n-r个。
(2)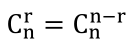 ,称为帕斯卡公式。可以用DP思路证明,取或不取第n个元素:若取第n个元素,则在剩下的n-1个元素中选r-1个;若不取第n个元素,则在剩下的n-1个元素中选r个。这个性质很有用,需要计算
,称为帕斯卡公式。可以用DP思路证明,取或不取第n个元素:若取第n个元素,则在剩下的n-1个元素中选r-1个;若不取第n个元素,则在剩下的n-1个元素中选r个。这个性质很有用,需要计算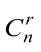 时,为避免阶乘计算,可利用这个递推关系。这个性质也用于构造帕斯卡三角(杨辉三角)。
时,为避免阶乘计算,可利用这个递推关系。这个性质也用于构造帕斯卡三角(杨辉三角)。
(3)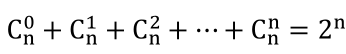 。这个表达式体现了组合数与二进制的关系,竞赛时常常用到。一个n位的二进制数,其数值范围为0~2n-1,共有2n个,每个二进制数就是一种组合。例如,n=4,r=2,有
。这个表达式体现了组合数与二进制的关系,竞赛时常常用到。一个n位的二进制数,其数值范围为0~2n-1,共有2n个,每个二进制数就是一种组合。例如,n=4,r=2,有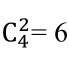 种组合,对应二进制数:0011、0101、0110、1001、1010、1100。
种组合,对应二进制数:0011、0101、0110、1001、1010、1100。
4. 多重集的排列和组合
如果S中的元素可以相同,称为多重集,如S={5×a,7×b,4×c}。下面给出多重集的排列和组合的定义。
(1) 无限多重集的排列:令S是一个多重集,它有k个不同的元素,每个元素都有无穷重复个数,那么S的r排列的个数为kr。
(2) 有限多重集的排列:令S是一个多重集,它有k个不同的元素,每个元素的重数分别为n1,n2,…,nk,S的大小为n=n1+n2+…+nk,则S的n排列的个数为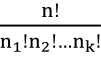 。
。
(3) 有限多重集的组合:令S是一个多重集,它有k个不同的元素,每个元素都有无穷重复个数,那么S的r组合的个数为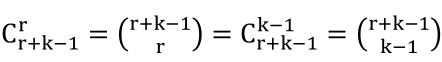 。
。
《算法竞赛》系列推文正在连载中,欢迎持续关注!

扫码优惠购书














