初等数论是数学的一个分支，它既古老又现代。最早的数论研究是从素数开始的，2000多年前欧几里得就发现了算术基本定理，即每个正整数可以按递增顺序唯一地写成素数的乘积。现代数论的发展始于高斯，他发明了同余，使研究整除关系时与研究方程一样方便。把素数从合数中分出来是数论的一个关键问题，发展了很多素性检验法；把正整数进行素因子分解是数论中的另一个核心问题；寻求方程的整数解是又一个重要内容。
威尔逊定理
威尔逊定理 若p为素数，则p可以整除(p-1)!+1。
威尔逊定理有多种表示方法，如下。
(1) ((p-1)!+1)mod p=0；
(2) (p-1)!mod p=p-1；
(3) (p-1)!=pq-1，q为正整数；
(4) 用同余表示为(p-1)! ≡-1(mod p)。
例如，5是素数，5可以整除(5-1)!+1=25。非素数不可以，如4不能整除(4-1)!+1=7。
下面用3道例题说明威尔逊定理的应用。
● 例6.26Zball in Tina Town(hdu 5391)
问题描述： 计算(n-1)! mod n。
输入： 第1行输入整数t，表示有t个测试；后面t行中，每行输入一个整数n。t≤105，2≤n≤109。
输出： 对每个n，输出(n-1)! mod n。
(1) 当n为合数时，除了4以外，(n-1)!中肯定有两个数的积为n，得(n-1)! mod n=0。
(2) 当n为素数时，根据威尔逊定理，(n-1)! mod n=n-1。
● 例6.27YAPTCHA(hdu 2973)
问题描述： 计算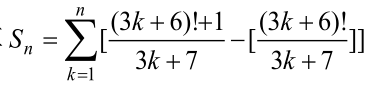
，其中［x］表示不大于x的最大整数。
输入：第1行输入整数t，表示有t个测试；后面t行中，每行输入一个整数n。1≤n≤106。
输出：对每个n，输出Sn。
设p=3k+7，记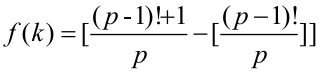
(1) 若p为合数，(p-1)!能被p整除，Sn=0。
(2) 若p为素数，(p-1)!=pq-1，有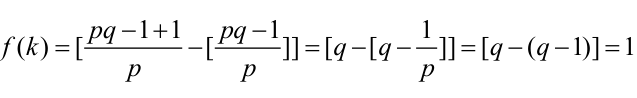
。
所以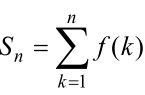
转换为求1~n内的素数个数。因为n不大，用素数筛即可。
● 例6.28Fansblog(hdu 6608)
问题描述： 给定一个素数p，找到比p小的最大素数q，输出q! mod p。
输入： 第1行输入整数t，表示有t个测试；后面t行中，每行输入一个整数p。109≤n≤1014。
输出： 对每个p，输出q! mod p。
先用Miller-Rabin素性测试找到q。根据威尔逊定理(p-1)! mod p=p-1，有q!(q+1)(q+2)…(p-1) mod p=p-1，即q! mod p=1/((q+1)(q+2)…(p-2)) mod p，需要用逆计算除法取模。
本题出现了对分数取模计算，分数取模是可计算的，根据费马小定理推出(b/a) mod m=(b am-2) mod m。例如，(2/5) mod 3=(2×53-2) mod 3=1。
《算法竞赛》系列推文正在连载中，欢迎持续关注！
扫码优惠购书
