
数据结构是数据的组织形式和访问方法,前文介绍了基础数据结构,在基础上发展出了很多高级数据结构,它们原理复杂,编程困难。
为什么需要这么多高级数据结构?这是在特定应用背景下高效处理数据的需要。基础数据结构不够强大,像数组、栈、队列这样的线性结构,计算复杂度为O(n),在面对大量数据时力不从心;二叉树、堆、哈希很高效,但是它们过于简单,在处理很多特定问题时操作不便。高级数据结构与某些应用背景紧密结合,能高效地解决问题。例如,集合问题用并查集;区间问题用树状数组、线段树、分块、莫队算法;混合问题用块状链表;动态查询用平衡树,等等。
本节详细介绍笛卡儿树的概念、实现方法、应用。
笛卡儿树的概念
Treap树的每个节点有两个属性:键值、随机的优先级。笛卡儿树(Cartesian Tree笛卡儿树(Cartesian Tree)是一种特殊的、简化的Treap树,它的每个节点的键值预先给定,但是优先级或者预先给定,或者随机生成。
笛卡儿树主要用于处理一个确定的数列。数列中的一个数有两个属性:在数列中的位置、数值。把位置看作键值,数值看作优先级,根据这个数列构造出来的笛卡儿树符合Treap树的两个特征如下。
(1) 以每个数的位置为键值,它是一棵BST。也就是说,对这棵树做中序遍历,返回的就是数列。
(2) 把数值看作Treap树的优先级,把数列建成一个堆。如果按大根堆建这棵树,那么在每个子树上,子树的根的权值是整棵子树上最大的。
图4.63给出一个用数列{2,7,6,24,8,15,5,11,19}建笛卡儿树的例子。
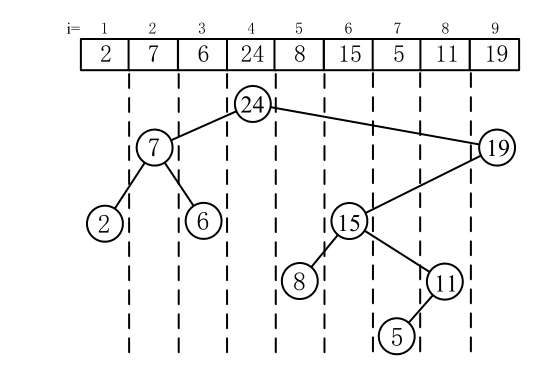
■ 图4.63用笛卡儿树存储数列
用单调栈建笛卡儿树
前面介绍的Treap树,若给定了每个节点的键值和优先级,那么Treap树的形态是唯一的。与之类似,笛卡儿树的形态也是唯一的。如何把数列建成一棵笛卡儿树?如果用前面Treap建树的做法,逐一加入节点,然后根据临时分配的优先级用旋转、分裂等操作调整形态,复杂度为O(log2n)。
笛卡儿树比普通Treap树简单,建树也更简单,有O(n)复杂度的建树方法。例如图4.64的例子,数列有5个数,从图4.64(a)到图4.64(d),逐一插入树上。
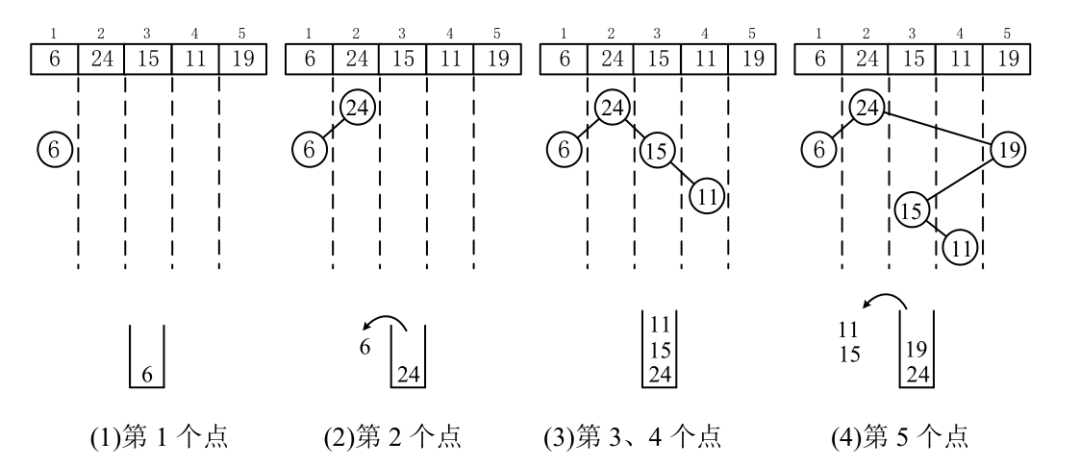
■ 图4.64借助单调栈建笛卡儿树
每次插入新的节点,横向的位置是固定的,新的点总是插入最右边,而且需要调整的是纵向位置,所以只需要考虑“最右链”,即从根开始一直沿着右儿子向下走的那条链。在最右链上,从上一个插入的点开始,按最大堆的要求寻找合适的纵向位置。新插入的节点,在插入结束之后,一定位于最右链的末端。
这个过程的实现用单调栈很容易操作。以大根堆为例,用栈维护从根开始的最右链,栈底最大,栈顶最小。例如,图4.64(c)中栈为{11,15,24},它是树上的右链,栈底是根24,栈顶是右链的末端11。
下面解释建树的步骤,从左到右把数字逐个插入树,并与栈中存储的右链节点比较。
(1) 插入第1个点6,6入栈。
(2) 插入第2个点24。24比栈顶的6(位于当前的右链上)大,弹出6,24入栈。6是24的左儿子。
(3) 插入第3个点15,15比栈顶24小,15入栈,15插入24的右子树;插入第4个点11,11比栈顶的15小,11入栈,11插入15的右子树。
(4) 插入第5个点19,19比栈顶11和15大,弹出11和15,然后19入栈,15是19的左儿子,19是24的右儿子。后面没有新的节点,结束。
在建树过程中,每个点入栈一次,出栈一次或不出栈,所以总复杂度为O(n),是最快的建树方法。
下面给出一道建树的例题。
● 例4.45Binary search heap construction(poj 1785)
问题描述: 建一棵笛卡儿树。给出n个点,每个点包括两个数据:标签label、优先级pri。把这n个点建成一棵笛卡儿树,并打印树。
输入: 每行是一个测试,输入的第1个数是节点数量n,后面有n个点,每个点包括标签和优先级。
输出: 打印树,每个节点的打印格式为(<left sub-treap><label>/<priority><right sub-treap>),中序打印。
输入样例:
7 a/3 b/6 c/4 d/7 e/2 f/5 g/1
输出样例:
(((a/3)b/6(c/4))d/7((e/2)f/5(g/1)))
下面给出了两种代码:buildtree()函数没有用栈,直接查最右链;buildtree2()函数用栈处理最右链。
第55行代码对标签(Treap树的键值)先排序,非常重要。排序之后,所有节点按从左到右的顺序插入树,插入时只需要在buildtree()函数中根据优先级调整。从这里也能认识到,笛卡儿树需要预先给出所有节点的键值,而优先级则不必,在建树时临时分配优先级也可以。当然,本题的优先级pri就是数列的数字本身,不需要临时分配。
//改写自:https://blog.csdn.net/qq_40679299/article/details/80395824#include<cstdio>#include<algorithm>#include<cstring>#include <stack>using namespace std;const int N = 50005;const int INF = 0x7fffffff;struct Node{char s[100]; int ls,rs,fa,pri;friend bool operator<(const Node& a,const Node& b){return strcmp(a.s,b.s)<0;}}t[N];void buildtree(int n){ //不用栈,直接查最右链for(int i=1;i<=n;i++){int pos = i-1; //从前一个结点开始比较,前一个结点在最右链的末端while(t[pos].pri < t[i].pri)pos = t[pos].fa; //沿着最右链一直找,直到pos的优先级比i大t[i].ls = t[pos].rs; //图(4):i是19,pos是24, 15调整为19的左儿子t[t[i].ls].fa = i; //图(4):15的父亲是19t[pos].rs = i; //图(4):24的右儿子是19t[i].fa = pos; //图(4):19的父亲是24}}void buildtree2(int n){ //用栈来辅助建树stack <int> ST; ST.push(0); //t[0]进栈,它一直在栈底for(int i=1;i<=n;i++){int pos = ST.top();while(!ST.empty() && t[pos].pri < t[i].pri){pos = t[ST.top()].fa;ST.pop(); //把比i优先级小的弹出栈}t[i].ls = t[pos].rs;t[t[i].ls].fa = i;t[pos].rs = i;t[i].fa = pos;ST.push(i); //每个结点都一定要进栈}}void inorder(int x){ //中序遍历打印if(x==0) return;printf("(");inorder(t[x].ls); printf("%s/%d",t[x].s,t[x].pri); inorder(t[x].rs);printf(")");}int main(){int n;while(scanf("%d",&n),n){for(int i=1;i<=n;i++){t[i].ls = t[i].rs = t[i].fa = 0; //有多组测试,每次要清零scanf(" %[^/]/%d", t[i].s, &t[i].pri); //注意输入的写法}t[0].ls = t[0].rs = t[0].fa = 0; //t[0]不用,从t[1]开始插结点t[0].pri = INF; //t[0]的优先级无穷大sort(t+1,t+1+n); //对标签先排序,非常关键。这样建树时就只需要考虑优先级pribuildtree(n); //buildtree2(n); 两种建树方法inorder(t[0].rs); //t[0]在树的最左端,第一个点是t[0].rsprintf("\n");}return 0;}
笛卡儿树和RMQ问题
笛卡儿树的最直接应用是RMQ问题。“笛卡儿树+LCA”也是一种求RMQ的方法。
建好笛卡儿树后,若查询区间[L,R]的RMQ,首先在树上找到L和R,L和R的LCA即为区间[L,R]的RMQ。建笛卡儿树的复杂度为O(n),在树上查找L和R复杂度约为O(log2n),然后用倍增法或Tarjan算法求LCA,总复杂度与ST算法、线段树差不多。不过,在笛卡儿树上查找L和R可能很耗时,因为笛卡儿树并不一定是一棵平衡的BST。
《算法竞赛》系列推文正在连载中,欢迎持续关注!

扫码优惠购书














