算法竞赛系列 | Treap树

清华计算机学堂 2023-03-24

386

数据结构是数据的组织形式和访问方法，前文介绍了基础数据结构，在基础上发展出了很多高级数据结构，它们原理复杂，编程困难。

为什么需要这么多高级数据结构？这是在特定应用背景下高效处理数据的需要。基础数据结构不够强大，像数组、栈、队列这样的线性结构，计算复杂度为O(n)，在面对大量数据时力不从心；二叉树、堆、哈希很高效，但是它们过于简单，在处理很多特定问题时操作不便。高级数据结构与某些应用背景紧密结合，能高效地解决问题。例如，集合问题用并查集；区间问题用树状数组、线段树、分块、莫队算法；混合问题用块状链表；动态查询用平衡树，等等。

本篇介绍Treap树。

Treap树也是一种原理比较简单的BST。Treap是一个合成词，把Tree和Heap各取一半组合而成，Treap是树和堆的结合，通常翻译成树堆。

Treap树的操作基于“键值+优先级”。BST的每个节点上存有一个元素，把元素的值称为“键值”，这是所有BST都有的。除此之外，Treap树为每个节点人为添加了一个称为优先级的权值。对于键值，这棵树是一棵BST；对于优先级，这棵树是一个堆。堆的特征是在这棵树的任意子树上，根节点的优先级最大。对于树上的任意一组节点：父亲fa、左孩子ls、右孩子rs，满足以下两个条件。

(1) 键值(key)满足BST的要求：ls.key≤fa.key≤rs.key。

(2) 优先级(pri)满足堆的要求：fa.pri≥max{ls.pri，rs.pri}。

提示/

Treap树的核心思想是用优先级维护二叉树的平衡性。

Treap树的性质

Treap树的重要性质：若每个节点的键值、优先级已经事先确定而且不同，那么建立的BST的形态是唯一的，与节点的插入顺序没有关系。可以把每个点的(键值，优先级)看作它在平面上的坐标(x，y)，坐标确定了它的位置。可简单地概括为节点的键值x限定了它在二叉树上的横向位置，优先级y限定了它的纵向位置。若优先级是随机产生的，那么在概率上就实现了二叉树的平衡。

下面用7个节点举例说明建树过程和Treap树的形态唯一性，如图4.58所示。节点的键值分别为{a，b，c，d，e，f，g}，优先级分别为{6，5，2，7，3，4，1}。图4.58(a)的纵向是优先级，横向是键值；图4.58(b)按BST的规则建了一棵树，从堆的角度看，它是一个最大堆(也可以用小根堆)；图4.58(c)是形成的Treap树。显然，由于每个节点被键值和优先级确定了位置，Treap树的形态是唯一的。

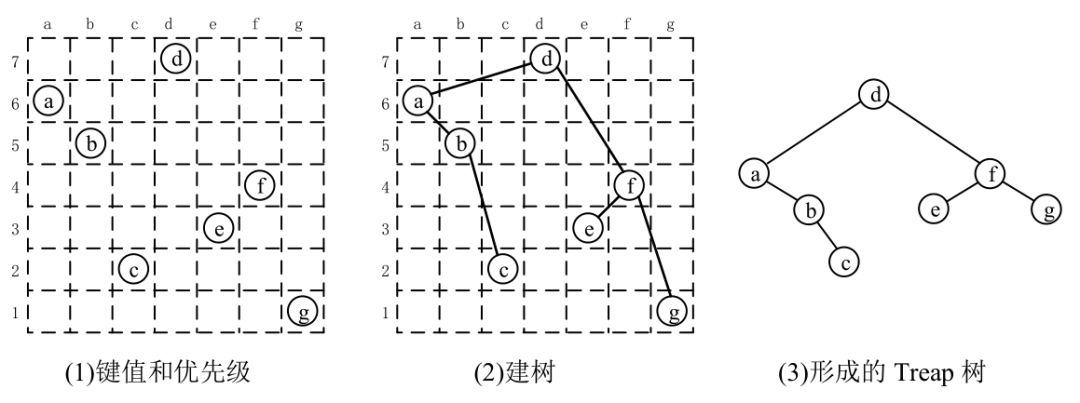
■ 图4.58Treap树的形态唯一性

需要注意，所谓“Treap树的形态唯一性”，是指已经提前确定所有节点的键值、优先级之后，建的树的形态是唯一的。但是在一般情况下，建Treap树是逐个点加入树上的，每个点的优先级是动态分配的，所以Treap树的最后形态并不能提前预知。不过，当处理完毕之后，这棵Treap树的新形态是确定唯一的。

给节点加上优先级是Treap树解决二叉树平衡的核心思想，合适的优先级能产生一个平衡的BST。如何产生优先级？最简单的方法是对每个节点的优先级进行随机赋值，那么生成的Treap树的形态也是随机的。虽然不能保证生成的Treap树是完美的平衡，但是从概率期望上看，它的插入、删除、查找的时间复杂度都为O(log₂n)。

如果预先知道所有节点的键值，那么建树很简单：先按键值排序，然后从键值最小的开始，从左到右逐个向树上加入节点，加入时按优先级(或者已知，或者随机生成)在纵向上调整形态。这就是笛卡儿树，它的建树复杂度为O(n)。

更常见的情况是需要动态加入新的节点，并不能预先知道键值和优先级。做法是每读入一个新键值，为它分配一个随机的优先级，插入树中，插入时动态调整树的结构，使它仍然是一棵Treap树。此时建一棵n个节点的树，复杂度为O(nlog₂n)。

如何调整和维护Treap树？有两种方法：①旋转法；②FHQ。两种方法的计算复杂度都为O(log₂n)。旋转法是经典方法，FHQ是近几年开始流行的新技术，FHQ不仅比旋转法编码简单，而且能用于区间翻转、移动、持久化等场合。

基于旋转法的Treap树操作

下面用旋转法实现几个基本操作：插入节点、删除节点、排名、第k大、前驱和后继。

1. 插入节点

把新节点k插入Treap树的过程有两步。

(1) 用朴素的插入方法，把k按键值大小插入一个空的叶子节点。

(2) 为k随机分配一个优先级，如果k的优先级违反了堆的性质，即它的优先级比父节点o高，那么让k向上走代替父节点o，得到一棵新的Treap树。

步骤(2)中的调整过程用到了一种技巧——旋转，包括左旋和右旋。观察图4.59，新节点k刚插入时，它有父节点o和子节点x、b。当k旋转到o的上面时，其他节点a、x、b保存原来的相对位置不变，以a、x、b为根的子树也随之同步移动。注意，不管是左旋还是右旋，树的中序遍历保持不变，这是BST的特征。

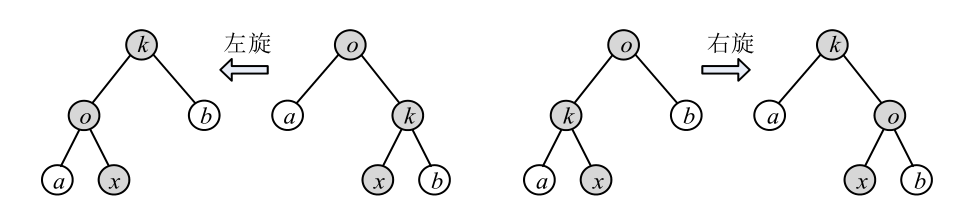
■ 图4.59Treap树的旋转(把k旋转到根)

旋转法插入节点的代码如下，代码中定义的节点名称o、k与图4.59的节点名称对应。

void rotate(int &o,int d){    //参考图示理解。d=0右旋，d=1左旋
    int k;
    if(d == 1) {              //左旋，把o的右儿子k旋到根部
        k = t[o].rs;          //rs: rson，右儿子
        t[o].rs = t[k].ls;    //图中的x
        t[k].ls = o;
    }
    else {                    //右旋，把o的左儿子k旋到根部
        k = t[o].ls;
        t[o].ls = t[k].rs;    //图中的x
        t[k].rs = o;
    }
  t[k].size = t[o].size;
  Update(o);
  o = k;                    //新的根是k
}

下面用一个例子说明插入的过程。设初始BST是{a，b，c}，插入新节点d。图4.60(a)是初始BST；图4.60(b)按键值找到空叶子，插入d；图4.60(c)中d的优先级比父节点c高，把c左旋，上升；图4.60(d)中d的优先级比新的父节点b高，继续左旋上升；4.60(e)再次左旋上升，完成了新的Treap树。注意在旋转的过程中，原来的节点a、b、c的相对位置保持不变。

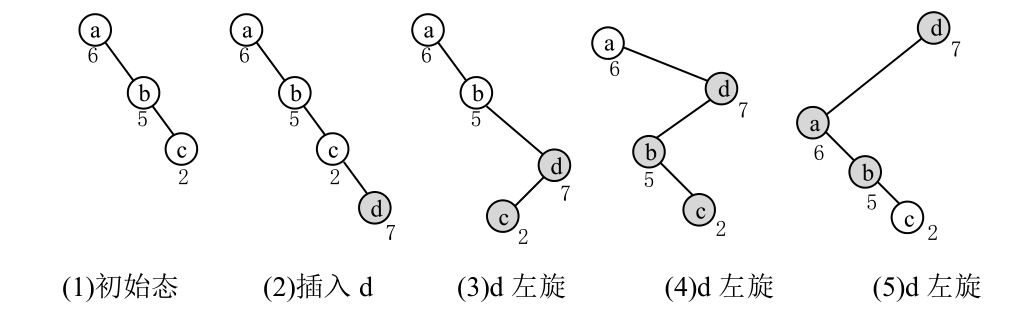
■ 图4.60Treap树的插入和调整

2. 删除节点

如果待删除的节点x是叶子节点，直接删除。如果待删除的节点x有两个子节点，那么找到优先级最大的子节点，把x向相反的方向旋转，也就是把x向树的下层调整，直到x被旋转到叶子节点，然后直接删除。

用旋转法处理Treap树的插入和删除，会不会导致出现一棵不平衡的Treap树？答案是不会，因为Treap的形态完全由留在树上的节点的键值和优先级决定，在概率上它仍然是平衡的。

3. 排名

“排名”和“求第k大数”一般被称为“名次树问题”，是BST的典型应用，在任何一种BST上都容易用递归遍历得到，Treap树也常用来求名次。它们都用到了节点的size值，即以这个节点为根的子树上的节点总数。

求数字x的排名。从根节点开始递归查找，递归到节点u时：若u的键值大于或等于x，x在u的左子树上，继续递归u的左子树；若u的键值小于x，x在u的右子树上，递归u的右子树，并加上u的左子树的size值。

4. 求第k大数

根据节点的size值不断递归整棵树，求得第k大数。

5. 前驱和后继

前驱是求比x小的数，后继是求比x大的数，计算过程与排名的过程类似。

用例4.41洛谷P3369给出Treap树代码，实现上述操作。

//洛谷P3369，用旋转法实现Treap树
#include<bits/stdc++.h>
using namespace std;
const int M=1e6+10;
int cnt = 0;             //t[cnt]: 最新结点的存储位置
struct Node{
int ls,rs;           //左右儿子
int key,pri;         // key：键值；pri：随机的优先级
int size;            //当前结点为根的子树的结点数量，用于求第k大和rank
}t[M];                   //tree[]，存树
void newNode(int x){     //初始化一个新结点
cnt++;        //从t[1]开始存储结点，t[0]被放弃。若子结点是0，表示没有子结点
t[cnt].size = 1;
t[cnt].ls = t[cnt].rs = 0;  //0表示没有子结点
t[cnt].key = x;             //key: 键值
t[cnt].pri = rand();        //pri：随机产生，优先级
}
void Update(int u){             //更新以u为根的子树的size
t[u].size = t[t[u].ls].size + t[t[u].rs].size+1;
}
void rotate(int &o,int d){      //旋转，参考图示理解。d=0右旋，d=1左旋
int k;
    if(d==1) {                  //左旋，把o的右儿子k旋到根部
       k=t[o].rs;
       t[o].rs=t[k].ls;//图中的x
       t[k].ls=o;
    }
    else {                      //右旋，把o的左儿子k旋到根部
       k=t[o].ls;
       t[o].ls=t[k].rs; //图中的x
       t[k].rs=o;
    }
t[k].size=t[o].size;
Update(o);
o=k;                       //新的根是k
}
void Insert(int &u,int x){
if(u==0){newNode(x);u=cnt;return;}    //递归到了一个空叶子，新建结点
t[u].size++;
if(x>=t[u].key)    Insert(t[u].rs,x); //递归右子树找空叶子，直到插入
else               Insert(t[u].ls,x); //递归左子树找空叶子，直到插入
if(t[u].ls!=0 && t[u].pri>t[t[u].ls].pri) rotate(u,0);
if(t[u].rs!=0 && t[u].pri>t[t[u].rs].pri) rotate(u,1);
Update(u);
}
void Del(int &u,int x){
t[u].size--;
if(t[u].key==x){
if(t[u].ls==0&&t[u].rs==0){u=0; return;}
if(t[u].ls==0||t[u].rs==0){u=t[u].ls+t[u].rs; return;}
if(t[t[u].ls].pri < t[t[u].rs].pri)
{     rotate(u,0); Del(t[u].rs, x); return;}
     else{ rotate(u,1); Del(t[u].ls, x); return;}
  }
  if(t[u].key>=x) Del(t[u].ls,x);
  else            Del(t[u].rs,x);
  Update(u);
}
int Rank(int u,int x){   //排名，x是第几名
  if(u==0)  return 0;
  if(x>t[u].key) return t[t[u].ls].size+1+Rank(t[u].rs, x);
  return Rank(t[u].ls,x);
}
int kth(int u,int k){    //第k大数是几?
  if(k==t[t[u].ls].size+1) return t[u].key;   //这个数为根
  if(k> t[t[u].ls].size+1) return kth(t[u].rs,k-t[t[u].ls].size-1);//右子树
  if(k<=t[t[u].ls].size)   kth(t[u].ls,k);    //左子树
}
int Precursor(int u,int x){
  if(u==0)   return 0;
  if(t[u].key>=x)  return Precursor(t[u].ls,x);
  int tmp = Precursor(t[u].rs,x);
  if(tmp==0)  return t[u].key;
  return tmp;
}
int Successor(int u,int x){
  if(u==0)   return 0;
  if(t[u].key<=x)  return Successor(t[u].rs,x);
  int tmp = Successor(t[u].ls,x);
  if(tmp==0)   return t[u].key;
  return tmp;
}
int main(){
  srand(time(NULL));
  int root = 0;           //root是整棵树的树根，0表示初始为空
  int n;  cin>>n;
  while(n--){
        int opt,x; cin >> opt >> x;
        switch (opt){
            case 1: Insert(root,x);    break;
            case 2: Del(root,x);       break;
            case 3: printf("%d\n",Rank(root,x)+1);    break;
            case 4: printf("%d\n",kth(root,x));       break;
            case 5: printf("%d\n",Precursor(root,x)); break;
            case 6: printf("%d\n",Successor(root,x)); break;
        }
  }
  return 0;
}