算法竞赛系列 | A*算法

A*搜索算法（A* Search Algorithm）可以高效率解决一类最短路径问题：给定一个确定起点、一个确定终点（或者可以预测的终点），求起点到终点的最短路径。A*算法常用于最短路径问题的求解，最短路问题的算法很多，例如双向广搜的效率也较高，而A*算法比双向广搜效率更高。另外，从本文的例题（K短路等）可以看出，A*算法可以解决更复杂的问题。注意，除了图这种应用场合，A*算法还能在更多场合下得到应用。

 A*算法用于最短路径问题时，可以概况为：A*算法 = 贪心最优搜索 + BFS + 优先队列。在图问题中，“Dijkstra + 优先队列”就是“BFS + 优先队列”，此时也可以把A*算法概况为：“A*算法 = 贪心最优搜索 + Dijkstra + 优先队列”。

A*算法的核心是估价函数f = g + h，它的效率取决于函数h的设计。

下面的内容，先介绍贪心最优搜索、Dijkstra与A*的关系，然后推理出A*的原理和应用。

1. 贪心最优搜索

贪心最优搜索（Greedy Best First Search）是一种启发式搜索，效率很高，但是因为使用了贪心的原理，不一定能得到全局最优解。

算法的基本思路是贪心：从起点出发，在它的邻居结点中选择下一个结点时，选那个到终点最近的结点。当然，实际上不可能提前知道到终点的距离，更不用说挑选出最近的邻居点了。所以，只能采用估计的方法，例如在网格图中，根据曼哈顿距离来估算邻居结点到终点的距离。

如何编程？仍然用“BFS + 优先队列”，不过，进入优先队列的，不是从起点s到当前点i的距离，而是从当前点i到终点t的距离。

很明显，贪心最优搜索避开了大量结点，只挑那些“好”结点，速度极快，但是显然得到的路径不一定最优。以边权为1的网格图为例，讨论两种情况：

（1）在无障碍的网格图中，贪心最优搜索算法的结果是最优解。因为用于估算的曼哈顿距离就是实际存在的最短路，所以每次找到的下一个结点，显然是最优的。

（2）在有障碍的网格图中，根据曼哈顿距离选下一跳结点，路线会一直走到碰壁，然后再绕路，最后得到的不一定是最短路径。

提示/

2. Dijkstra（BFS）

用优先队列实现的Dijkstra（BFS），能比较高效地求得一个起点到所有其他点的最短路径。Dijkstra算法有BFS的通病：下一步的搜索是盲目的，没有方向感。即使给定了终点，Dijkstra也需把几乎所有的点和边放进优先队列进行处理，直到终点从优先队列弹出为止。所以它适合用来求一个起点到所有其他结点的最优路径，而不是只求到一个终点的路径。 

提示/

A*算法是贪心最优搜索和Dijkstra的结合，“既看起点，又看终点”。A*算法比Dijkstra快，因为它不像Dijkstra一样盲目。A*算法比贪心搜索准确，它不仅有贪心搜索的预测能力，而且能得到最优解。

A*算法是如何结合这两个算法的？

设起点是s，终点是t，算法走到当前位置i点，把s-t的路径分为两部分：s-i-t。

（1）s-i的路径，由Dijkstra保证最优性；

（2）i-t的路径，由贪心搜索进行预测，选择i的下一个结点；

（3）当走到i碰壁时，i将被丢弃，并回退到上一层重新选择新的点j，j仍由Dijkstra保证最优性。

 以上思路可以用一个估价函数来具体操作：

 f(i) = g(i) + h(i)

 f(i)是对i点的评估，g(i)是从s到i的代价，h(i)是从i到t的代价。

若g = 0，则f = h，A*就退化为贪心搜索；

若h = 0，则f = g，A*就退化为Dijkstra。

A*每次根据最小的f(i)来选择下一个点。g(i)是已经走过的路径，是已知的；h(i)是预测未走过的路径；所以f(i)的性能取决于h(i)的计算。

A*算法的复杂度，在最差情况下是Dijkstra（或者BFS+队列），一般情况下会更优。

A*算法的最优性。A*算法的最终结果是最优的吗？答案是确定的，它的解和Dijkstra的解一样，是最短路径。当i到达终点t时，有h(t) = 0，那么f(t) = g(t) + h(t) = g(t)，而g(t)是通过Dijkstra求得的最优解，所以在终点t这个位置，A*算法的解是最优的。

提示/

下面的图3.9准确地对比了Dijkstra、贪心最优搜索、A*这三种算法的区别。图中起点是s，终点是t，黑格是障碍。这张图精心设置了障碍的位置，以演示三种算法是如何绕过障碍的。 

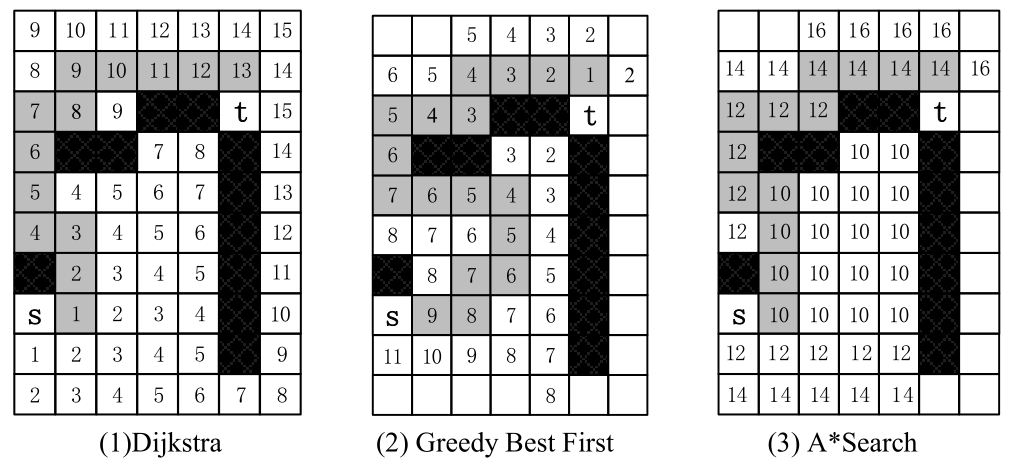
■ 图3.9 三个算法对比

从这三张格子图可以比较三种算法的计算量。图中无数字的空白格子是算法不需要遍历的格子，空白格子越多，计算量越少。图(1)的Dijkstra算法遍历了所有的格子，计算量最大；图(2)的贪心最优搜索的空白格子最多，计算量最少；图(3)的A*搜索计算量居中。

三个算法都基于"BFS+优先队列"。有数字的格子是搜索过的结点，并进入优先队列处理。灰色阴影格是最后得到的一条完整路径。格子中的数字是距离，按曼哈顿距离计算。

（1）Dijkstra（BFS）算法。格子中的数字，是从起点s到这个格子的最短距离。算法搜索格子时，把这些格子到起点的距离送入优先队列，当弹出时，就得到了s到这些格子的最短路径。最后，当终点t从优先队列弹出时，即得到s到t的最短距离14。

（2）贪心最优搜索。格子中的数字，是从这个格子到终点t的曼哈顿距离。读者可以仔细分析它的工作过程，这里简单说明如下：从s沿最小曼哈顿距离，一直走到碰壁处的2；2从优先队列弹出后，剩下最小的是3；3弹出后，剩下最小的是4；......；持续这个过程，那些看起来更近但是最终碰壁的结点被逐个弹走，直到拐过障碍，最后到达t。得到的路径共走了18步，不是最优路径。

（3）A*搜索。某个格子i中的数字，是“s到i的最短路 + i到t的曼哈顿距离”。算法在扩展格子的过程中，标记数字的格子都会进入优先队列。在图示中，先弹出所有标记为10的格子，再弹出标记为12的格子，直到最后弹出终点t。最后得到的s-t最短路径也是14。

如何打印出完整的一条路径？三个算法都基于BFS，而BFS记录路径是非常简单的：在结点u扩展邻居点v的时候，在v上记录它的前驱结点u，即可以从v回溯到u；到达目的后，从终点逐步回溯到起点，就得到了路径。在Dijkstra算法中，每次从优先队列中弹出的，都是得到了最短路径的结点，从它们扩展出来的邻居结点，也会继续形成最短路径，所以能根据前驱和后继结点的关系，方便地打印出一条完整的最短路径。A*算法用Dijkstra算法来确定前驱后继的关系，也一样可以打印出一条最短路径。贪心最优搜索的路径打印最简单，就是普通BFS的路径打印。

在二维平面的图问题中，有下面3种方法可以近似计算h。下面的(i.x, i.y)表示i点的坐标，(t.x, t.y)表示终点t的坐标。

（1）曼哈顿距离。应用场景：只能在四个方向（上，下，左，右）移动。

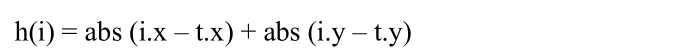
（2）对角线距离。应用场景：可以在八个方向上移动，例如国际象棋的国王的移动。

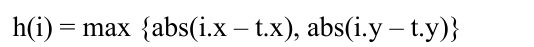
（3）欧几里得距离。应用场景：可以向任何方向移动。

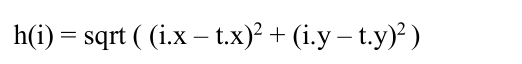
非平面问题，需要设计合适的h函数，后面的例题中有一些比较复杂的h函数。

设计h时注意以下三条基本规则： 

（1）g和h应该用同样的计算方法。例如h是曼哈顿距离，g也应该是曼哈顿距离。如果计算方法不同，f = g + h就没有意义了。

（2）根据应用情况正确选择h。各个结点的h值，应该能正确反映它们到终点的距离远近。例如下一跳结点有2个选项：A(280, 319)、B(300, 300)，如果用曼哈顿距离应该选A，用欧氏距离应该选B。如果只能走四个方向（需要按曼哈顿距离计算路径），用欧式距离计算就会出错。

（3）h应该优于实际存在的所有路径。前面的例子中，h(i)小于等于i-t的所有可能路径长度，也就是说，最后得到的实际路径，长度一定大于等于h(i)。这个规则可以用下面两点讨论来说明。

h(i)比i-t的实际存在的最优路径长。假设这条实际的最优路径是path，由于程序是根据h(i)来扩展下一个结点的，所以很可能会放弃path，而选择另一条非最优的路径，这会造成错误。

h(i)比i-t的所有实际存在的路径都短。此时i-t上并不存在一条长度为h(i)的路径，如果程序根据h(i)来扩展下一结点，最后肯定会碰壁；但是不要紧，程序会利用BFS的队列操作弹走这些错误的点，退回到合适的结点，从而扩展出实际的路径，所以仍能保证正确性。

这三个基本规则中第（3）点最重要，应用A*算法时应特别注意。

A*算法的主要难点是设计合适的h函数，而编码很容易。例如图问题中，Dijkstra或BFS使用g函数，A*使用f = g + h函数，那么编码时只要用f代替g即可。读者可以尝试把图论的最短路径题目改成用A*算法实现，例如poj 2243。

下面给出两道复杂一点的例题。

K短路问题是A*算法应用的经典例子，几乎完全套用了A*算法的估价函数。

下面分别用暴力法和A*算法求解。

（1）暴力法：BFS + 优先队列

用BFS搜索所有的路径，用优先队列让路径按从短到长的顺序输出。“BFS+优先队列”求最短路，在“BFS+优先队列”这一节中曾讲解过。其原理是当再次扩展到某个点i时，如果这次的新路径比上次到达i的路径更短，就替代它；优点队列可以让结点按路径长短先后输出，从而保证最优性。队列的元素是一个二元组(i, dist(s-i))，即结点i和路径s-i的长度。

BFS求所有路径，就是最简单的“BFS + 优先队列”，再次扩展邻居i时，计算它到s的距离，然后直接进队列，并不与上次i进队列的情况进行比较。一个结点i会进入优先队列很多次，因为可以从它的多个邻居分别走过来；每一次代表了一个从s到i的路径。优先队列可以让这些路径按dist从短到长的顺序输出，i从优先队列中第x次弹出，就是s到i的第x个短路。对于终点t，统计它出队列的次数，第K次时停止，这就是第K短路。

在K短路问题中，路径有可能形成环路。有的题目允许环路，有的不允许。如果允许环路，那么想在环路上绕多少圈都可以，环路上的结点反复进入队列，K可以无限大。  在最短路算法中并不需要判断环路，因为更新操作有去掉环路的隐含作用。

复杂度：因暴力法需要生成几乎所有的路径，而路径数量是指数增长的，所以暴力法的复杂度非常高。

下面用一个简单的图3.10解释BFS暴力搜索所有路径的过程。

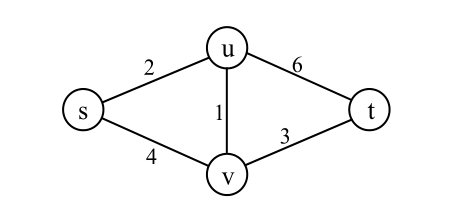
■ 图3.10 一个简单图

下面的表格给出了算法的步骤。结点后面的下标表示从s到这个结点的路径长度，例如u2，表示二元组(u, 2)，即结点u，以及s-u的路径长度2。步骤中没有列出环路。

■ 表3.2  K短路的队列

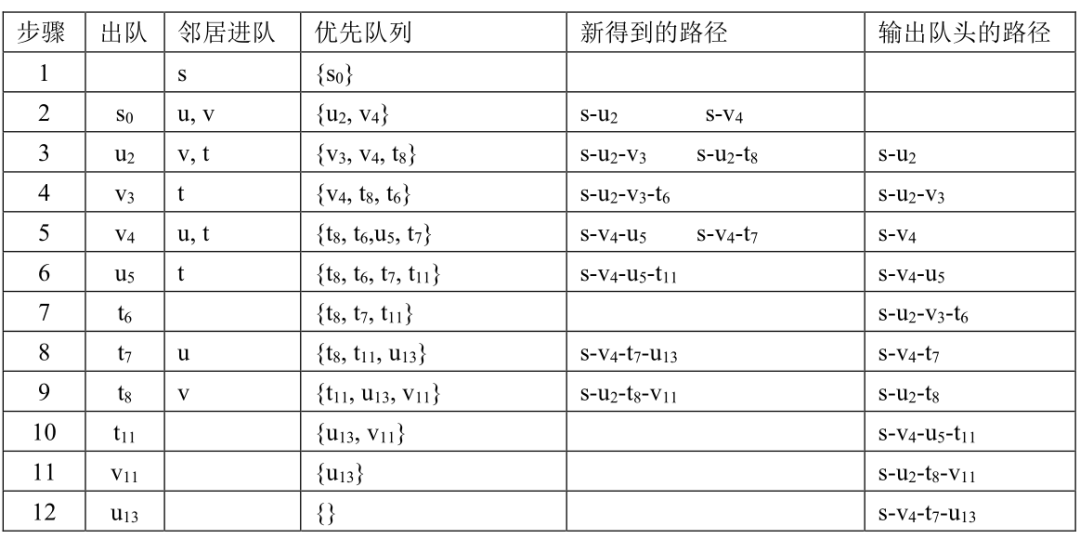
从第二列的“出队”可以看到，共产生10个路径，按从短到长的顺序排队输出。从起点s到终点t共有4条路径，t在第7、8、9、10步出队的时候，输出了第1、第2、第3、第4路径。表格中也列出了s到每个结点的多个路径和它们的长度，例如s-u有3个路径，s-v有3个路径。

（2）A*算法求K短路

从暴力法可以知道：从优先队列弹出的顺序，是按这些结点到s的距离排序的；一个结点i从优先队列第x次弹出，就是s-i的第x短路；终点t从队列中第K次弹出，就是s-t的第K短路。

如何优化暴力法？是否可以套用A*算法？

联想前面讲解A*算法求最短路的例子，A*算法的估价函数f(i) = g(i) + h(i)，g是从起点s到i的距离，h是i到终点t的最短距离（例子中是曼哈顿距离）。那么在K短路问题中，可以设计几乎一样的估价函数。g(i)仍然是起点s到i的距离；而h(i)，只是把曼哈顿距离改为从i到t的最短距离。这个最短距离如何求？用Dijkstra算法，以终点t为起点反推，求所有结点到t的最短距离即可。

编程非常简单。仍用暴力法的“BFS+优先队列”，但是在优先队列中，用于计算的不再是g(i)，而是f(i)。当终点t第K次弹出队列时，就是第K短路。

根据前面对A*算法原理的解释，求K短路的过程将得到很大优化。虽然在最差情况下，算法复杂度的上界仍是暴力法的复杂度，但优化是很明显的。

下面再看一道例题。

下面是两种解题方法。

（1）BFS+剪枝。这一题是典型的BFS。从{a, b}可以转移到8种情况，即{2a, a}、{2a, b}、{2b,a}、{2b,b}等等。把每种{a, b}看成一个状态，那么1个状态可以转移到8个状态。编码时，再加上去重和剪枝。此题P不是太大，“BFS+剪枝”可行。

（2）A*算法。如何设计估价函数f(i) = g(i) + h(i) ？g(i)是从初始态到i状态的步数。h(i)是从i状态到终点的预期步数，它应该小于实际的步数。如何设计呢？容易观察到，{a, b}中的较大数，一直乘以2递增，是最快的。例如样例中的31，在起点状态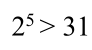，，经5步可以超过目标值，所以h = 5。