算法竞赛系列 | 贪心法与拟阵

清华计算机学堂 2023-03-16

673

本篇的基本算法原理简单，代码易写，但是效率很高，是常用的编码技术，广泛应用于编程和竞赛中，做题时不妨先想想能否结合这些算法。

贪心法的效率非常之高，复杂度常常为O(1)，几乎是计算量最小的算法。不过，贪心法是一种局部最优的解题方法，而很多问题都需要求全局最优，所以在使用贪心法之前需要评估是否能从局部最优推广到全局最优。拟阵是一种评估方法，能在某些特殊情况下证明贪心法是全局最优的。

贪心法

贪心(Greedy)可以说是最容易理解的计算机算法思想,因为贪心在日常生活中太常见了。简单地说，贪心就是“走一步看一步”“只看眼前，不管将来”。作为算法的贪心，它的执行过程是把整个问题分解成多个步骤，在每个步骤都选取当前步骤的最优方案，直到所有步骤结束；在每步都不考虑对后续步骤的影响；在后续步骤中也不再回头改变前面的选择，也就是不“悔棋”。

有些高级算法是基于贪心思想的，如最小生成树算法、单源最短路径Dijkstra算法、哈夫曼编码等，在本书相关章节中有详细解释。

下面用最少硬币问题的例子引导出贪心法的应用规则。

最少硬币问题：某人带着3种面值的硬币去购物，假设有1元、2元、5元的面值，硬币数量不限；他需要支付M元，问怎么支付，才能使硬币数量最少？

根据生活常识，第1步应该先拿出面值最大的5元硬币，第2步拿出面值第2大的2元硬币，最后才拿出面值最小的1元硬币。在这个解决方案中，硬币数量总数是最少的。

下面是最少硬币问题的代码，输入金额，输出3种面值硬币的数量。

#include<bits/stdc++.h>
using namespace std;
const int n = 3;
int coin[] = {1,2,5};
int main(){
    int i, money;
    int ans[n] = {0};            //记录每种硬币的数量
    cin >> money;                //输入钱数
    for(i= n-1; i>=0; i--){          //求每种硬币的数量
        ans[i] = money/coin[i];
        money = money - ans[i]*coin[i];
    }
    for(i= n-1; i>=0; i--)
        cout << coin[i]<<": "<<ans[i]<<endl; //输出每种面值硬币的数量
    return 0;
}

从上面的例子可以看出，贪心法代码的计算量极小，贪心法差不多是计算复杂度最优的算法了。

上面例子的最后结果是最优的。虽然每步选硬币的操作并没有从整体最优来考虑，而是只在当前步骤选取了局部最优，但是结果是全局最优的。

但是，局部最优并不总是能导致全局最优，如这个最少硬币问题，用贪心法一定能得到最优解吗？稍微改换一下参数，就不一定能得到最优解，甚至在有解的情况下也无法算出答案。

(1) 不能得到最优解的情形。例如，硬币面值比较奇怪，有1、2、4、5、6元。现在需支付9元，如果用贪心法，答案是6+2+1，需要3个硬币，而最优的5+4只需要两个硬币。

(2) 算不出答案的情形。例如，如果有面值1元的硬币，能保证用贪心法得到一个解，如果没有1元硬币，常常得不到解。例如，只有面值为2、3、5元的硬币，需支付9元，用贪心法无法得到解，但解是存在的：9=5+2+2。

所以，在最少硬币问题中，是否能使用贪心法与硬币的面值有关。如果是1、2、5元这样的面值，贪心法是有效的，而对于1、2、4、5、6元或2、3、5元这样的面值，贪心法是无效的。

提示/

任意面值硬币问题的标准解法是动态规划。如果用贪心无法求最优解，往往能用动态规划求最优解。

虽然贪心法不一定能得到最优解，但是它思路简单，编程容易。因此，如果一个问题确定用贪心法能得到最优解，那么应该使用它。

如何判断能用贪心法？贪心法求解的问题需要满足以下特征。

(1) 最优子结构性质。当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质，也称此问题满足最优性原理。也就是说，从局部最优能扩展到全局最优。

(2) 贪心选择性质。问题的整体最优解可以通过一系列局部最优的选择得到。

贪心法没有固定的算法框架，关键是如何选择贪心策略。贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。

另外，即使用贪心法得不到最优，其结果“虽然不是最好，但是还不错”。某些难解问题，如旅行商问题，很难得到最优解，但是用贪心法常常能得到不错的近似解。如果一个问题不一定非要求得最优解，那么试试贪心法，往往有不错的结果。

贪心法在一些算法中有应用，如爬山法、模拟退火、A*搜索等。

贪心法看起来似乎不靠谱，因为不知道结果是不是全局最优。有没有一个一般性的数学理论，可以证明一个问题能用贪心法？有一个叫作“拟阵”的理论，虽然它不能覆盖所有贪心法适用的情况，但是在很多情况下可以确定贪心法能产生最优解。

拟阵

拟阵理论(Matroid Theory)是一种组合优化理论。如果一个问题满足拟阵结构，那么贪心能得到最优解。本节对拟阵和贪心法的关系做简单介绍。

一个拟阵是满足以下条件的一个序对M=(S，L)。

(1) S是一个有穷集合，如S={1，2，5，10}。

(2) L是S的一个非空子集族，L中的元素称为拟阵的独立集，如L={ {1}，{2}，{5}，{1，2}，{1，5}，{2，5}}，L中有6个独立集。

(3) M满足遗传性。对于独立集B，若B∈L，对于任意A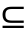B，有A∈L。例如B={2，5}，A={2}，那么A∈L。

(4) M满足交换性。对于任意A∈L，B∈L，且|A|<|B|(|A|表示A中元素的个数)，有某个元素x∈B-A，使A∪{x}∈L。这一条也称为独立扩充公理。例如，A={2}，B={2，5}，x=5，那么A∪{x}={2，5}∈L。

若L中的一个独立集A不能扩充，称A为极大独立集。在上面的例子中，L的极大独立集有3个：{1，2}，{1，5}，{2，5}。

定理2.10.1同一拟阵的极大独立集的元素个数相同。

用反证法证明：设A和B为拟阵的两个大小不同的极大独立集，且|A|<|B|，根据拟阵的交换性，A是可扩充的，不满足最大独立集的定义，与假设矛盾，故命题成立。

拟阵和贪心法有什么关系？可以把贪心问题转换为求权值最大的独立集。下面用伪代码说明。

对拟阵M=(S，L)，赋予S的每个元素x一个正整数权值w(x)，定义S的子集A的权值wA=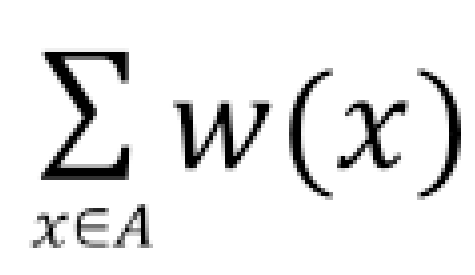，即元素的权值和。显然，权值最大独立集一定是极大独立集。求这个权值最大独立集的伪代码如下。

Greedy(S,L,w)           //拟阵M =(S, L)与权值函数w
    A={}                //A初始化为空集
    sort S by w         //将S内的元素x按权值w(x)从大到小降序排序
    for x in S:         // 按w(x)大到小的顺序，遍历每一个x∈S
      if(A∪{x}∈L)  
           A=A∪{x}
    return A;           //返回权值最大独立集