全文链接：http://tecdat.cn/?p=26277

尾部指数的希尔HILL统计量估计。更具体地说，我们看到如果 ， 和 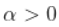，然后希尔HILL估计为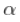  

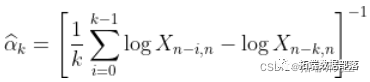
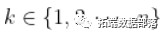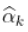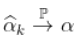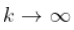 。然后  在某种意义上满足某种一致性  ,如果 ，即 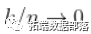 （在收敛速度的附加假设下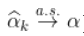， ）。此外，在附加的技术条件下

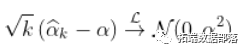
为了说明这一点，请考虑以下代码。首先，让我们考虑一个帕累托生存函数，以及相关的分位数函数

> Q=fuction(p){unro(funion(x) S(x)-(1-p),loer=1,per=1e+9)$root}

我们将考虑更复杂的生存函数。这是生存函数和分位数函数，

> plot(u,Veie(Q)(u),type="l")

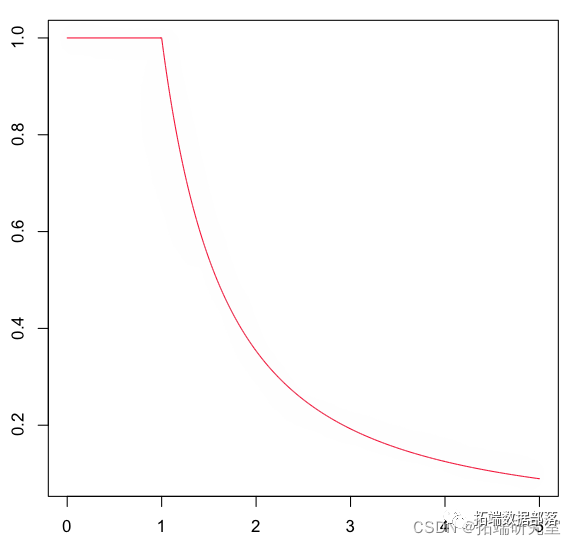
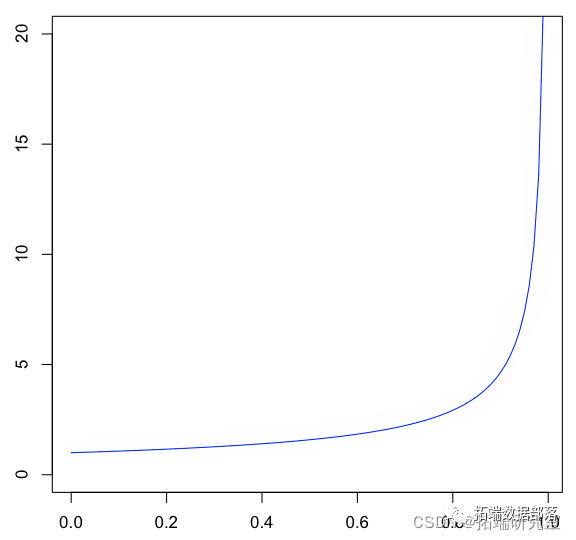
在这里，我们需要 分位数函数从这个分布中生成一个随机样本，

> X=Vectorize(Q)(runif(n))

hill统计量在这里

> abline(h=alpha)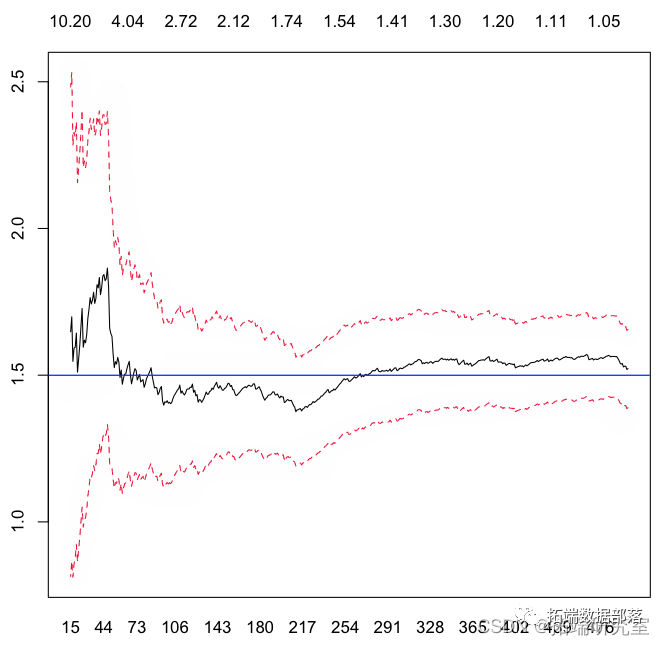

---

点击标题查阅往期内容

POT超阈值模型和极值理论EVT分析

左右滑动查看更多

01

02

03

04

我们现在可以生成数千个随机样本，并查看这些估计器（对于某些特定的k）。

> for(s in 1:ns){
+ X=Vectorize
+ H=hill
+ hilk=function(k) 
+ HilK\[s,\]=Vectorize
+ }

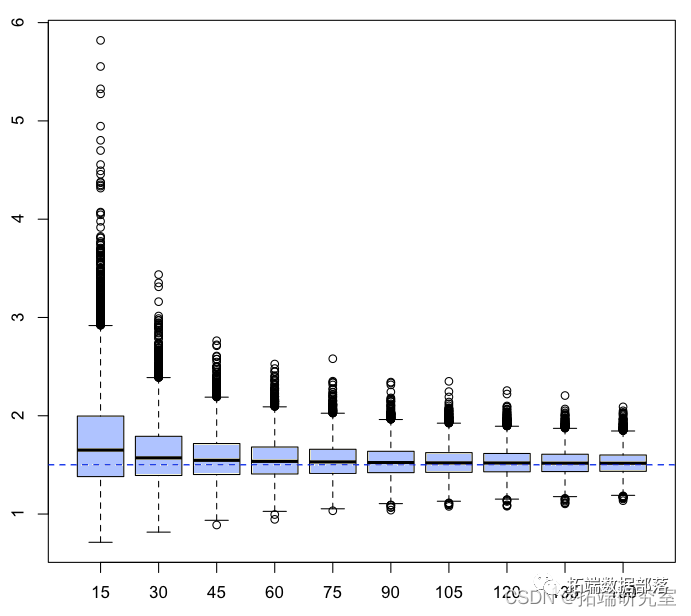
如果我们计算平均值，

> plot(15*(1:10),apply(2,mean)

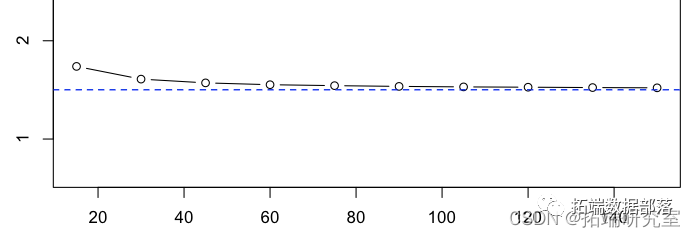
我们得到了一系列可以被认为是无偏的估计量。

现在，回想一下，处于 Fréchet 分布并不意味着 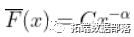， 和 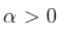, 但意味着

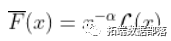
对于一些缓慢变化的函数 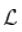，不一定恒定！为了了解可能发生的情况，我们必须稍微具体一些。这只能通过查看生存函数的性质。假设，这里有一些辅助函数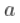  

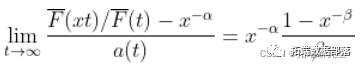
这个（正）常数 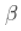 以某种方式与生存函数与幂函数之比的收敛速度有关。

更具体地说，假设

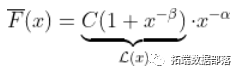
然后，使用获得二阶正则变化性质 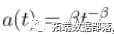，然后，如果  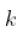趋向于无穷大太快，那么估计就会有偏差。 如果 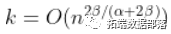，那么，对于一些 ,

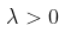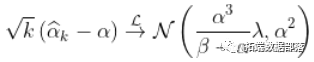
这个结果的直观解释是，如果 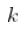 太大，并且如果基础分布不_完全_ 是帕累托分布，那么希尔估计量是有偏的。这就是我们所说的意思

• 如果 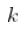 太大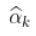，  是有偏估计量

• 如果 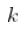 太小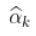，  是一个不稳定的估计量

（后者来自样本均值的属性：观察越多，均值的波动性越小）。

让我们运行一些模拟以更好地了解正在发生的事情。使用前面的代码，生成具有生存函数的随机样本实际上是极其简单的

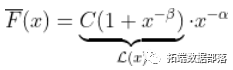
> Q=function(p){uniroot(function(x) S(x)-(1-p)}

如果我们使用上面的代码。

希尔hill变成

> abline(h=alpha)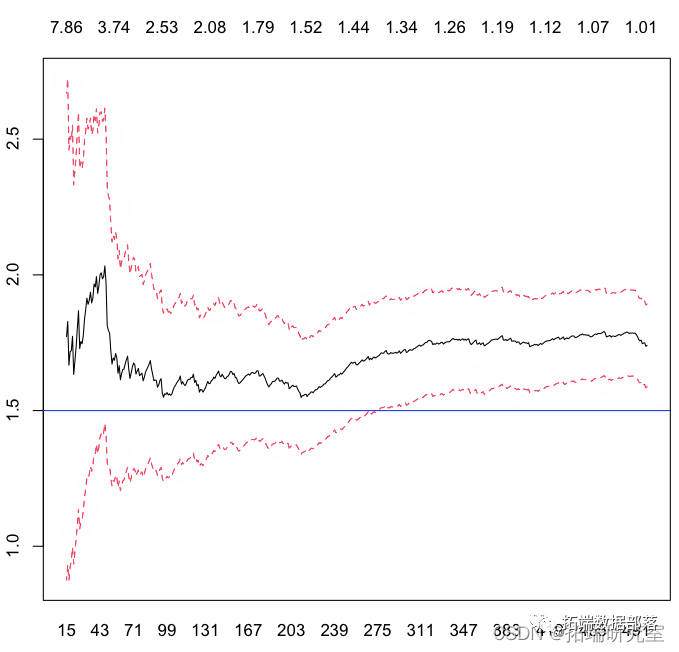

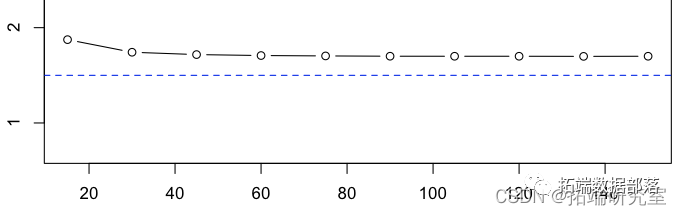
但它仅基于一个样本。再次考虑数千个样本，让我们看看 Hill 统计量如何，

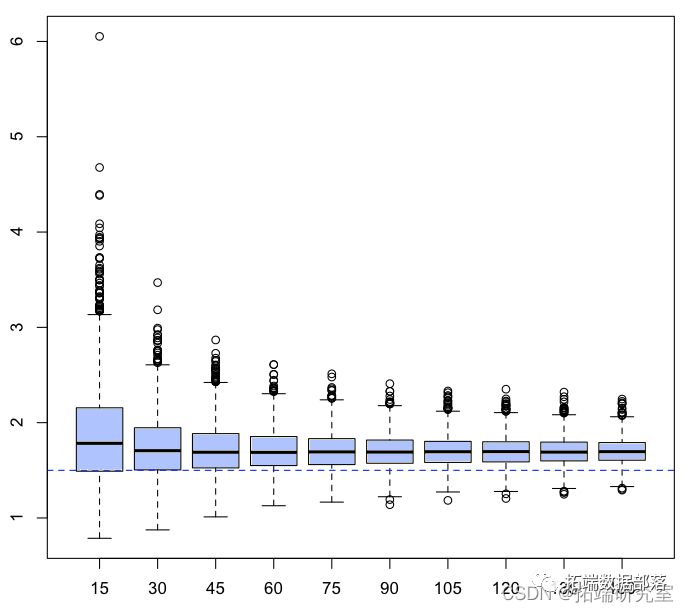
所以这些估计量的（经验）平均值是

点击文末“阅读原文”

获取全文完整资料。