原文链接：http://tecdat.cn/?p=18087
方差分析是一种常见的统计模型，顾名思义，方差分析的目的是比较平均值（点击文末“阅读原文”获取完整代码数据）。
为了说明该方法，让我们考虑以下样例，该样例为学生在硕士学位课程中的最终统计考试成绩（分数介于0到20之间）。
相关视频
这是我们的因变量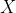 
。“分组”变量将是学生参加辅导课的方式，采用“自愿参与”，“非自愿参与”的方式。最后是“不参与”（不参加或拒绝参加的学生）。为了形成组，我们有两个变量。第一个是学生的性别（“ F”和“ M”），第二个是学生的身份（取决于他们是否获得许可）。
> tail(base)
PART GEN ORIG NOTE
112 vol F R1 16.50
113 non_vol. M R1 11.50
114 non_vol. F R1 10.25
115 non_vol. F R1 10.75
116 non_vol. F a 10.50
117 vol M R1 15.75
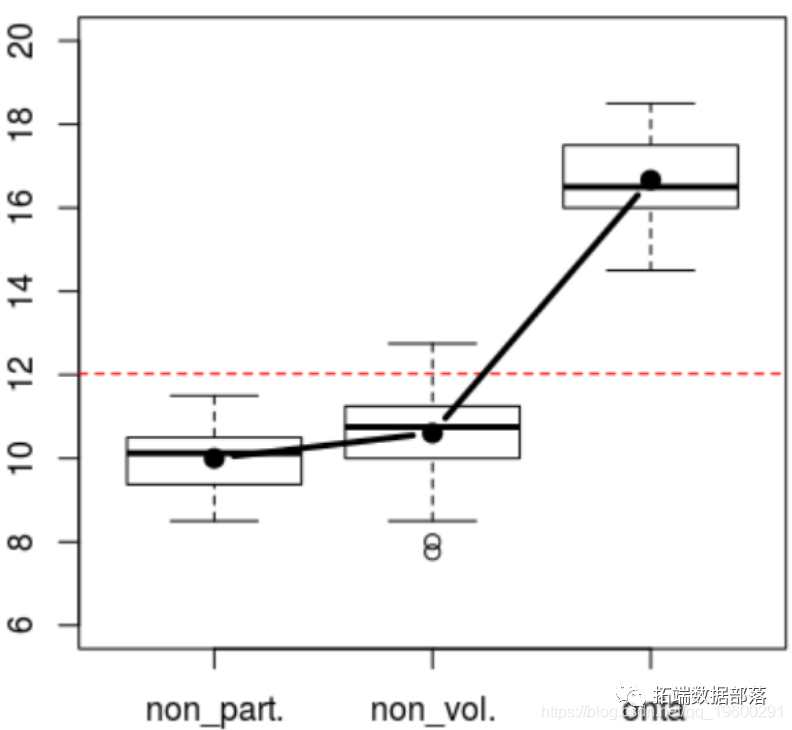
在开始多因素分析之前，让我们从单因素分析开始。我们可以查看分数的变化，具体取决于分组变量
> boxplot(base$NOTE~base$PAR
> abline(h=mean(base$NOTE),lty=2,col="re
点击标题查阅往期内容
左右滑动查看更多
我们还可以根据性别来查看
> boxplot(NOTE~GEN,ylim=c(6,20))
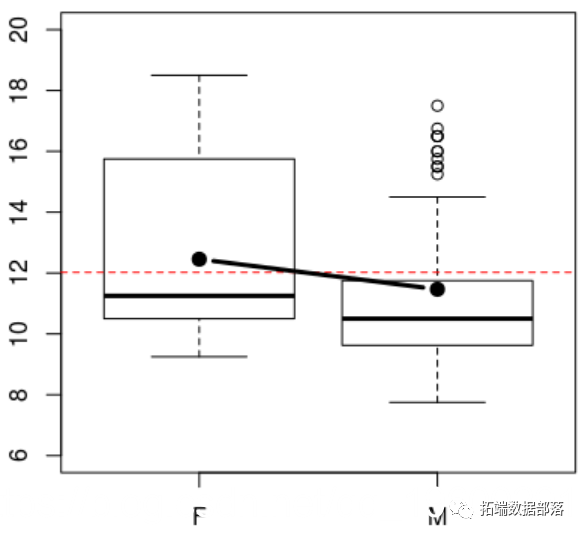
在方差分析中，假设 !（这里的图裂啦，重新上传下哦）
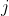指定可能的处理方式（这里有3种）。
我们将考虑对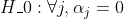 
作为补充假设 
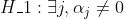。然后，我们将估计两个模型。
第一个是约束模型。
> sum(residuals(lm(NOTE~1,data=base))^2)
[1] 947.4979
对应于
> (SCR0=sum((base$NOTE-mean(base$NOTE))^2))
[1] 947.4979
第二，我们进行回归，
> sum(residuals(lm(NOTE~PART,data=base))^2)
[1] 112.5032
当我们与子组的平均值进行比较时，就等于查看了误差，
>
> (SCR1=sum((base$NOTE-base$moyNOTE)^2))
[1] 112.5032
费舍尔的统计数据
> (F=(SCR0-SCR1)*(nrow(base)-3)/SCR1/(3-1))
[1] 423.0518
判断我们是否处于接受或拒绝假设的范围内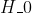 
，可以看一下临界值，它对应于费舍尔定律的95％分位数，
> qf(.95,3-1,nrow(base)-3)
[1] 3.075853
由于远远超过了这个临界值，我们拒绝 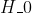。我们还可以计算p值
> 1-pf(F,3-1,nrow(base)-3)
[1] 0
在这里（通常）为零。它对应于我们通过函数得到的
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 423.05 < 2.2e-16 ***
Residuals 114 112.50 0.99
---
或者
Terms:
PART Residuals
Sum of Squares 834.9946 112.5032
Deg. of Freedom 2 114
Residual standard error: 0.9934135
Estimated effects may be unbalanced
可以总结为
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 423.05 < 2.2e-16 ***
Residuals 114 112.50 0.99
---
我们在这里可以看到分数并非独立于分组变量。
我们可以进一步挖掘。Tukey检验提供“多重检验”，它将成对地查看均值的差异，
Tukey multiple comparisons of means
95% family-wise confidence level
$PART
diff lwr upr p adj
non_vol.-non_part. 0.60416 -0.04784 1.2561 0.07539
volontaire-non_part. 6.66379 5.92912 7.3984 0.00000
volontaire-non_vol. 6.05962 5.54078 6.5784 0.00000
我们在这里看到，“非自愿”和“非参与”之间的差异不显着为非零。或更简单地说，假设我们将接受零为零的假设。另一方面，“自愿”参加的得分明显高于“非自愿”参加或不参加的得分。我们还可以成对查看学生的检验，
Pairwise comparisons using t tests with pooled SD
data: NOTE and PART
non_part. non_vol.
non_vol. 0.03 -
volontaire <2e-16 <2e-16
如果我们将“非自愿”和“非参与”这两种方式结合起来，并将这种方式与“自愿”方式进行比较，我们最终将对平均值进行检验，
Welch Two Sample t-test
data: NOTE[PART == "volontaire"] and NOTE[PART != "volontaire"]
t = 29.511, df = 50.73, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
5.749719 6.589231
sample estimates:
mean of x mean of y
16.66379 10.49432
我们看到，我们在这里接受了“志愿者”学生的成绩与其他学生不同的假设。
在继续之前，请记住在模型中
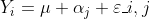在某种意义上说，与对应于同调模型 
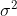不依赖分组 。
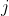我们可以使用Bartlett检验（该检验将检验方差的同质性）来检验该假设，请记住，如果p值超过5％，则假设“方差齐整性”得到了验证
Bartlett test of homogeneity of variances
data: base$NOTE and base$PART
Bartlett's K-squared = 0.5524, df = 2, p-value = 0.7587
更进一步，我们可以尝试对性别进行方差分析的两因素分析，通常要根据我们的分组情况，也可以根据性别对变量进行分析。当均值的形式为零时，我们将讲一个没有相互作用的模型 
，我们可以包括我们考虑的交互
总的来说，我们的模型
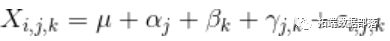
其中，按实验处理方式表示与观察到的平均值平均值的偏差，而按组表示与所观察到的平均值平均值的偏差。这样可以通过添加一些约束来识别模型。最大似然估计：
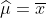
对应于总体平均值
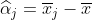
对应于每次实验的平均值（或更确切地说，它与总体平均值的偏差），
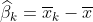
最后
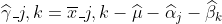
是
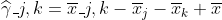
我们对一组进行方差分析
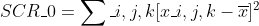
对于约束模型，
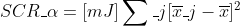
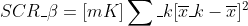
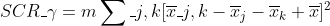
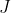和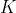 
表示实验次数和组数
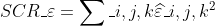
方差分解公式在这里给出
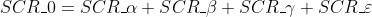
我们将进行手动计算，
Terms:
PART GENRE PART:GENRE Residuals
Sum of Squares 834.9946 20.9618 3.4398 88.1017
Deg. of Freedom 2 1 2 111
Residual standard error: 0.8909034
Estimated effects may be unbalanced
总结结果
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 526.0081 < 2.2e-16 ***
GENRE 1 20.96 20.96 26.4099 1.194e-06 ***
PART:GENRE 2 3.44 1.72 2.1669 0.1194
Residuals 111 88.10 0.79
---
由于实验组与对照组之间似乎没有任何交互作用，因此可以将其从方差分析中删除。
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 515.364 < 2.2e-16 ***
GENRE 1 20.96 20.96 25.875 1.461e-06 ***
Residuals 113 91.54 0.81
---
从结果可以看到（自愿）参加课程会有所帮助。
点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言方差分析（ANOVA）学生参加辅导课考试成绩差异》。
点击标题查阅往期内容
