引言

故名思义，就是把两个代表同一个类型的事物的不同长度序列进行时间上的“对齐”。比如 DTW 最常用的地方，语音识别中，同一个字母，由不同人发音，长短肯定不一样，把声音记录下来以后，它的信号肯定是很相似的，只是在时间上不太对整齐而已。所以我们需要用一个函数拉长或者缩短其中一个信号，使得它们之间的误差达到最小。

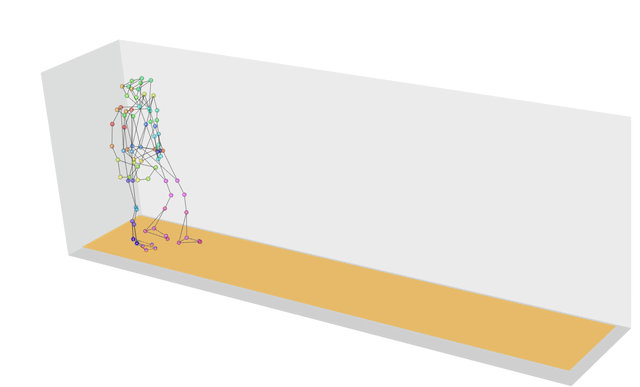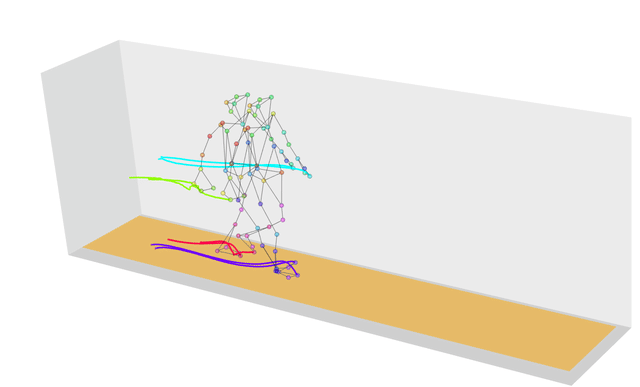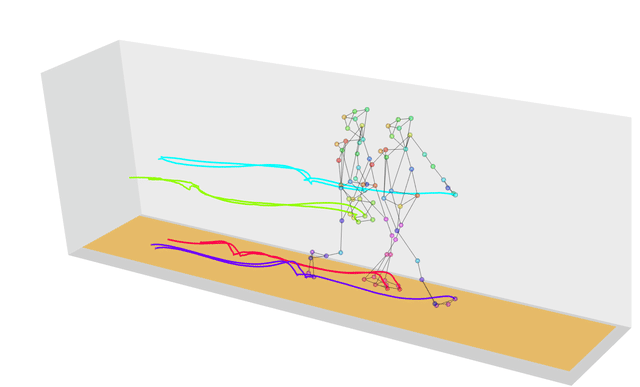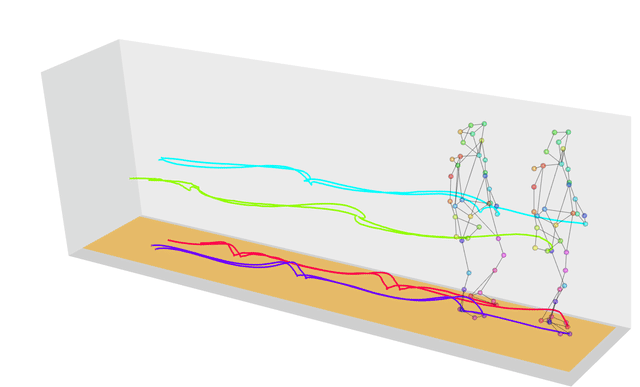
再来看看运动捕捉，比如当前有一个很快的拳击动作，另外有一个未加标签的动作，我想判断它是不是拳击动作，那么就要计算这个未加标签的动作和已知的拳击动作的相似度。但是呢，他们两个的动作长度不一样，比如一个是 100 帧，一个是 200 帧，那么这样直接对每一帧进行对比，计算到后面，误差肯定很大，那么我们把已知拳击动作的每一帧找到无标签的动作的对应帧中，使得它们的距离最短。这样便可以计算出两个运动的相似度，然后设定一个阈值，满足阈值范围就把未知动作加上“拳击”标签。

欧氏距离与 DTW

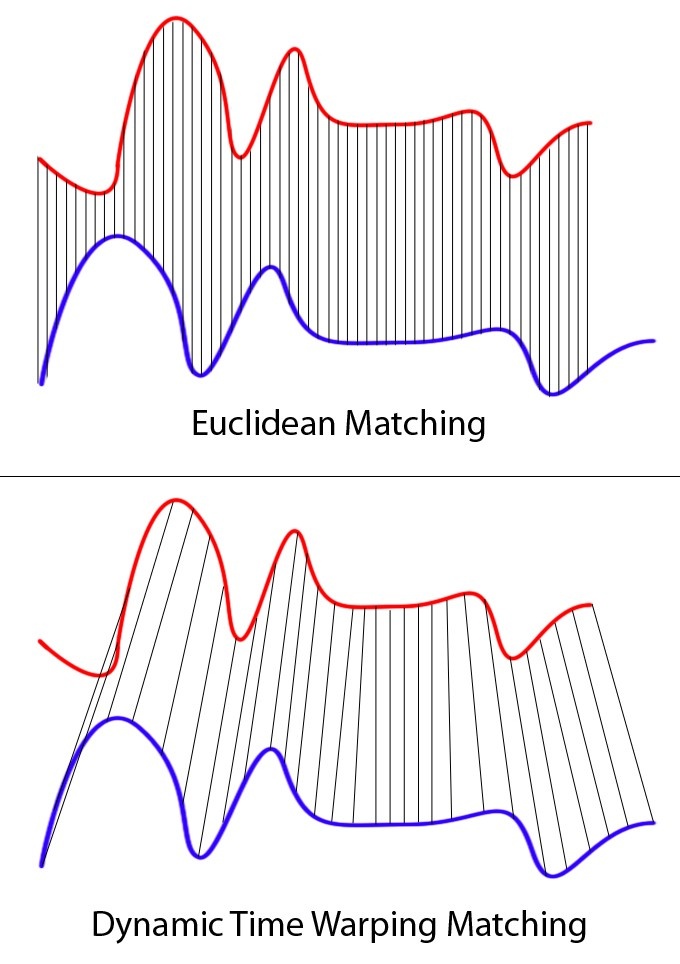
描述两个序列之间的相似性，欧氏距离是一种十分简单且直观的方法，但对于序列之间 out of phase 的情况，计算欧氏距离得到的结果会比实际的最小距离大很多，比如下面两个几乎一样的序列：

左边是欧氏距离的对应关系，在同一时刻上的点相互对应，计算总距离；右边是DTW的点对应关系，可以看到，下面序列某时刻的点可以对应上面序列非同一时刻的点，同时一个点可以对应多个点，多个点也可以对应一个点，也就是说每个点尽可能找离它距离最小的点，允许时间轴上的伸缩。显而易见的，这种情况下 DTW 计算的距离比欧氏距离更小。因此对于时间上有拉伸或压缩的序列，使用 DTW 计算的序列距离更加合理，因此该算法在语音序列匹配中使用十分广泛。

主要思想

给定两个时间序列 和 ，它们的长度分别是 和 。先画一个 的二维数组 ，数组中的每个点 代表 与 的距离 .

DTW 的核心思想是在这样的一个距离矩阵中从两个序列的起点找到通往两个序列终点（即对角线的一端到另一端）的最小距离路径，但是在寻找路径的过程中，必须满足一些约束条件：

• 边界条件：起点必须是 ，终点必须是 ，要有始有终；
• 连续性：若 ，则路径的下一个点 需要满足

即，不可能跨过某个点去匹配，只能和自己相邻的点对齐。这样可以保证 和 中的每个坐标都在 中出现。

• 单调性：如果 ，那么对于路径的下一个点 需要满足

这限制 上面的点必须是随着时间单调进行的。综合连续性和单调性约束，每一个格点的路径就只有三个方向。如: 如果路径已经通过了格点 ，那么下一个通过的格 点只可能是下列三种情况之一:

满足上面这些约束条件的路径可以有指数个，然后我们感兴趣的是使得下面的规整代价最小的路径:

示例

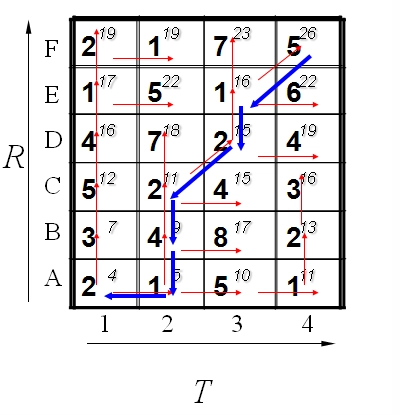
假设标准模板 R 为字母 ABCDEF (6个)，测试模板 T 为 1234 (4个)。R 和 T 中各元素之间的距离已经给出。如下：

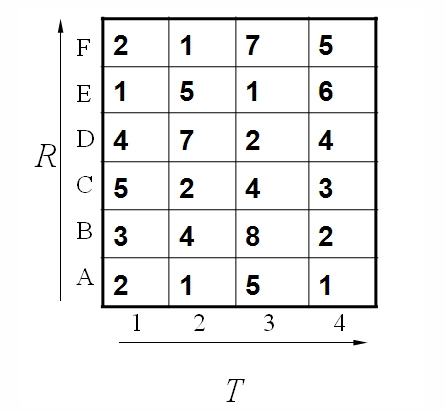
我们需要找出其中距离最短的那条匹配路径。

现假设题目满足如下的约束：当从一个方格 或 中到下一个方格 ，如果是横着或者竖着的话其距离为 ，如果是斜着对角线过来的则是 。

我们将所有的匹酉步骤标注后如下:

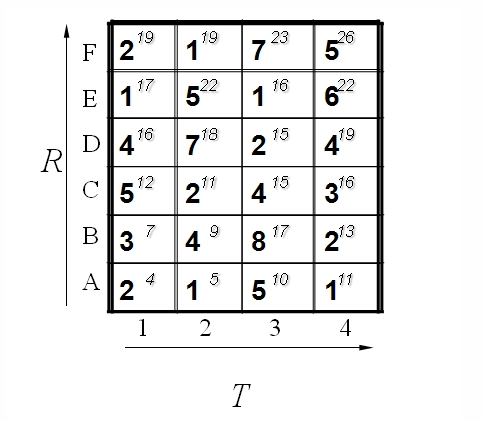
路径如下图：