在统计学中,斯皮尔曼等级相关系数(英语:Spearman's rank correlation coefficient 或 Spearman's ), 经常以希腊字母 或以 表示,此相关系数以查尔斯·斯皮尔曼之名命名。它是衡量两个变量的依赖性的无母数指标。它利用单调方程评价两个统计变量的相关性。若数据中没有重复值,且当两变量完全单调相关时,斯皮尔曼相关系数为 +1 或 −1 。
定义和计算
斯皮尔曼相关系数被定义成等级变量之间的皮尔逊相关系数。对于样本容量为 的样本, 个原始数据 被转换成等级数据 , 相关系数 为
其中等级数据 是每个原始数据的降序位置的平均。如下表所示:
| 变量 | 降序位置(仅示意,不使用) | 降序位置的平均 (使用) |
|---|---|---|
| 0.8 | 5 | 5 |
| 1.2 | 4 | |
| 1.2 | 3 | |
| 2.3 | 2 | 2 |
| 18 | 1 | 1 |
实际应用中, 变量间的连结是无关紧要的, 于是可以通过简单的步骤计算 ,被观测的两个变量的等级的差值 , 则 为
相关度量
度量一对观测数据的统计依赖性还有其他的几种度量指标: 在相关性和依赖性中有谈及。其中最常用的是皮尔逊积矩相关系数。
斯皮尔曼相关也可称为 “级别相关”;也就是说, 被观测数据的“等级” 被替换成 “级别”。在连续的分布中, 被观测数据的级别,通常总是小于等级的一半。然而,在这个案例中,级别和等级相关系数是一致的。更一般的, 被观测数据的“级别” 与估计的总体样本的比值小于给定的值,即被观测值的一半。也就是说,它是相应的等级系数的一种可能的解决方案。虽然不常用, “级别相关”还是仍然有被使用。
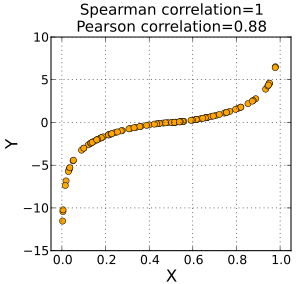
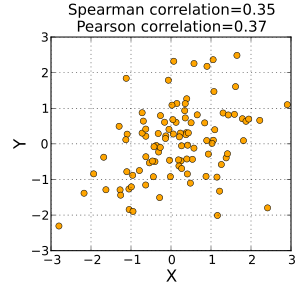
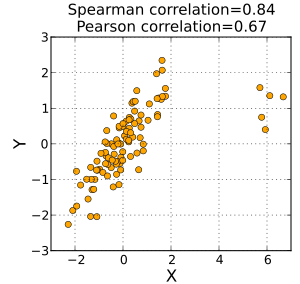
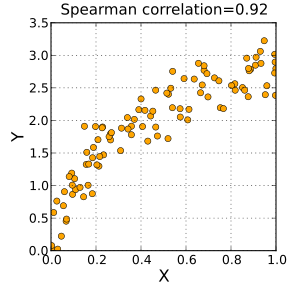
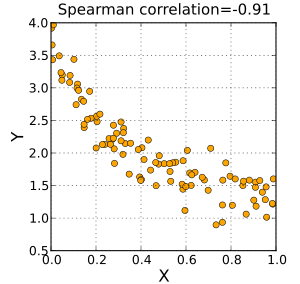
示例
在此例中,我们要使用下表所给出的原始数据计算一个人的智商和其每周花在电视上的小时数的相关性。
| 智商, | 每周花在电视上的小时数, |
|---|---|
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
首先,我们必须根据以下步骤计算出 ,如下表所示。
排列第一列数据 。创建新列 并赋以等级值 。 然后,排列第二列数据 . 创建第四列 并相似地赋以等级值 。 创建第五列 保存两个等级列的差值 和 . 创建最后一列 保存 的平方.
| 智商, | 每周花在电视上的小时数, | 的排名 | 的排名 | ||
|---|---|---|---|---|---|
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
根据 计算 。样本容量n为 10。将这些值带入方程
得 ...
这个值很大表明上述两个变量的关系很小。原始数据不能用于此方程中,相应的, 应使用皮尔逊相关系数计算等级。
文章转载自稷殿下,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






