再生核希尔伯特空间

函数空间

欧几里得空间、希尔伯特空间、巴拿赫空间或者是拓扑空间，这些我们经常见到的学术名词都属于函数空间。在数学中，函数空间是从集合 到集合 的给定种类的函数的集合。它叫做空间是因为在很多应用中，它是拓扑空间或向量空间或这二者^[1]。

一言以蔽之，函数空间由集合和定义在其上的函数组成。

与集合相对应的是集合中的元素，把集合中的元素由一个集合映射到另一个集合需要通过不同的操作。

要明白这些函数空间的定义首先得从距离，范数，内积，完备性等基本概念说起。

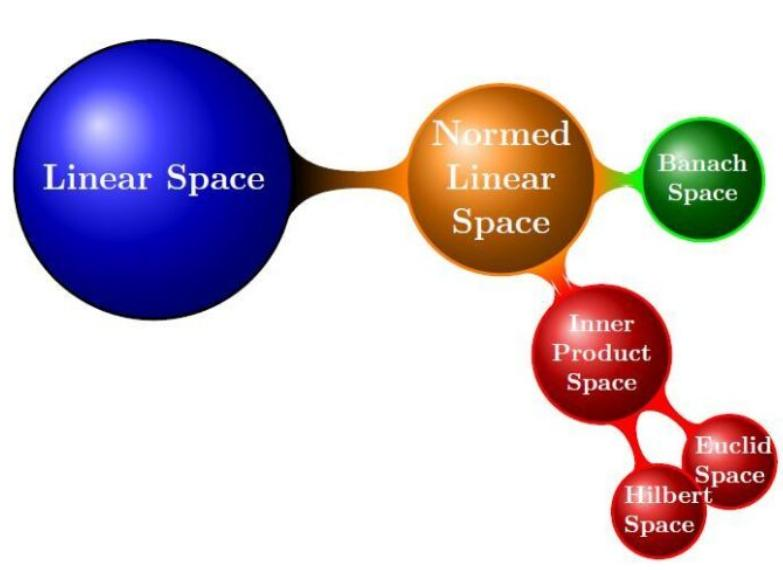
• 线性空间（Linear space）

线性空间又称作向量空间，关注的是向量的位置，对于一个线性空间，知道基（相当于三维空间中的坐标系）便可确定空间中元素的坐标（即位置）；线性空间只定义了加法和数乘运算。

• 赋范线性空间（Normed linear space）

如果我们想知道向量的长度怎么办？—-定义范数，引入赋范线性空间，其定义了范数的线性空间。

• 内积空间（Inner product space）

如果我们想知道向量的夹角怎么办？—-定义内积，引入内积空间，其定义了内积的线性空间。

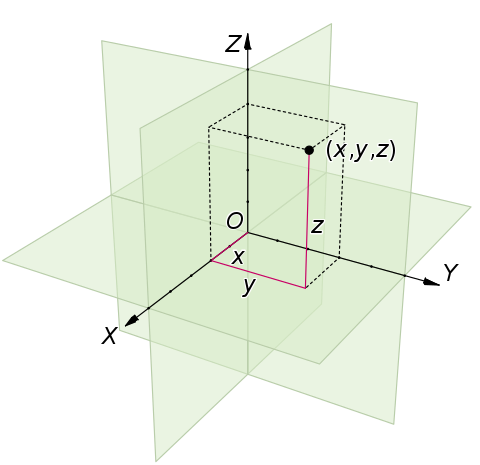
• 欧式空间（Euclid space）

如果我们想研究收敛性（极限）怎么办？—-定义完备^[2]定义了内积的有限维实线性空间。

有限维^[3]   设 是线性空间 的一个线性无关子集，我们设 的维度为 。当 时，称 为有限维的，否则称 为无限维的，即欧式空间中没有无限维的计算的概念。

• 巴纳赫空间（Banach space）

完备的赋范线性空间。

完备空间^[4]   完备度量空间或者完备空间是具有下述性质的空间：空间中的任何柯西序列都收敛在该空间之内。如在有理数集上的一个序列{1，1.4，1.41，1.414，1.4142…}，可知此序列极限为 ，而 为无理数，不属于有理数集，即有理数集不具备完备性，也就是有理数集不具备极限的概念，因为有理数集上的数都是确定的。

• 希尔伯特空间（Hilbert space）

希尔伯特空间是完备的内积空间，空间中每个元素都是一个函数。

在数学里，希尔伯特空间（Hilbert space）即完备
的内积空间
，也就是一个带有内积的完备向量空间^[5]。希尔伯特空间是有限维欧几里得空间的一个推广，使之不局限于实数的情形和有限的维数，但又不失完备性（而不像一般的非欧几里得空间那样破坏了完备性）。

再生核希尔伯特空间（Reproducing Kernel Hilbert Space，RKHS）

首先引入再生核的概念：

集合 ， 是定义在 上的希尔伯特空间，则 满足：
1. 对于 ， 作为 的函数属于空间 ；
2. 对于 ，，都有 。
则称   为 的再生核。

将 作为一组正交基构建一个 希尔伯特空间 , 这个空间中的任何一个函数（向量） 都可以表示为这组基的线性组合。如

则 就可以表示为 中的一个无限维的向量: ， 表示二元函数或无限维矩阵， 就可以表示矩阵第 行的一元函数或无限维向量，也就是固定核函数的一个参数为 ，那么

同样的，

因此，

以上就是核的可再生性(reproducing)，即用核函数来再生两个函数的内积。也被叫做可再生核希尔伯特空间.

再生核希尔伯特空间是支持监督学习（SVM）等监督学习模型的理论基础，实际上再生核希尔伯特空间就是是由核函数构成的希尔伯特空间。再生性指的就是原本函数之间计算内积需要算无穷维的积分（也就是这个映射函数可以映射到高维甚至无穷维（高斯核），而计算无穷维的积分是非常复杂的），但是现在只需要算核函数可以。

小结

距离⟶范数⟶内积
向量空间+范数⟶ 赋范空间+线性结构⟶线性赋范空间+内积运算⟶内积空间+完备性⟶希尔伯特空间
内积空间+有限维⟶欧几里德空间
赋范空间+完备性⟶巴拿赫空间

参考资料