承接上文^[1]，希尔伯特空间（Hilbert space，）是完备的内积空间。傅里叶变换的底层是希尔伯特空间坐标变换^[2]，本文将从希尔伯特空间坐标系变换角度解释傅里叶变换。

希尔伯特空间坐标变换

这里在无穷维的空间讨论问题，如果这个无穷维的空间对内积是完备的，那么这个空间就是希尔伯特空间。

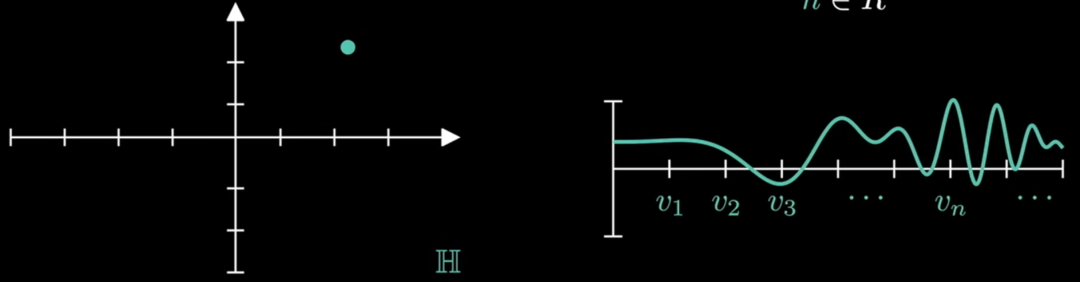
首先要对二维平面的一个点 升维到无穷维得到 。

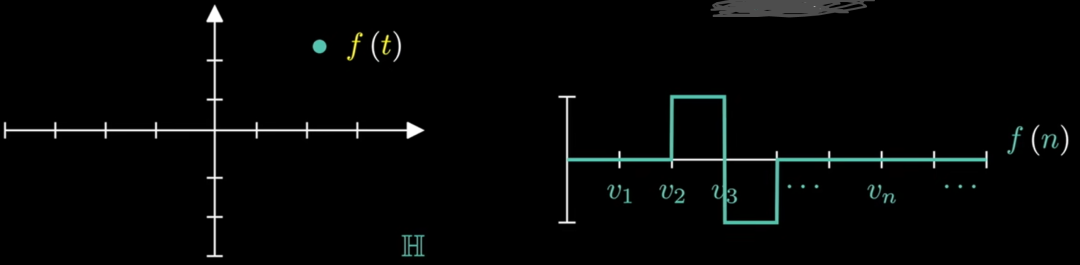
把无穷个坐标轴 排列起来看作横轴，把无穷维空间的一个点向无穷个坐标轴投影得到的取值可以看作纵轴。那么，无穷维空间中的一个点就可以与一个二维平面内的一条函数曲线 一一对应。

<<< 左右滑动见更多 >>>

不止是二维空间，升维的目的就是将有限维空间（欧式空间）中的一条函数曲线降维成无穷维空间中的一个点。

<<< 左右滑动见更多 >>>

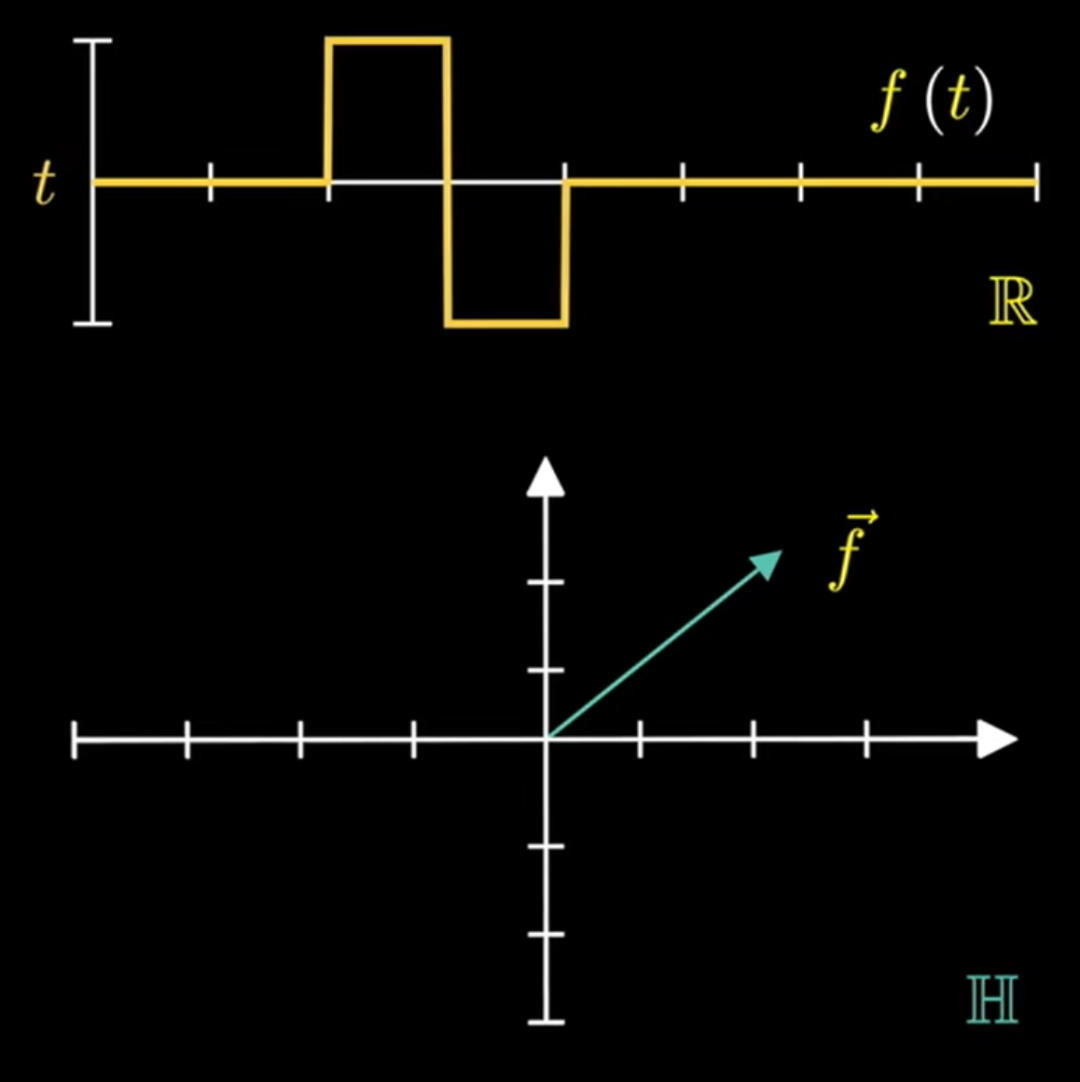
无穷维空间的一个点还可以使用向量等价表示，也就是说，二维空间的一个函数 可以由无穷维空间中的一个向量 相对应。

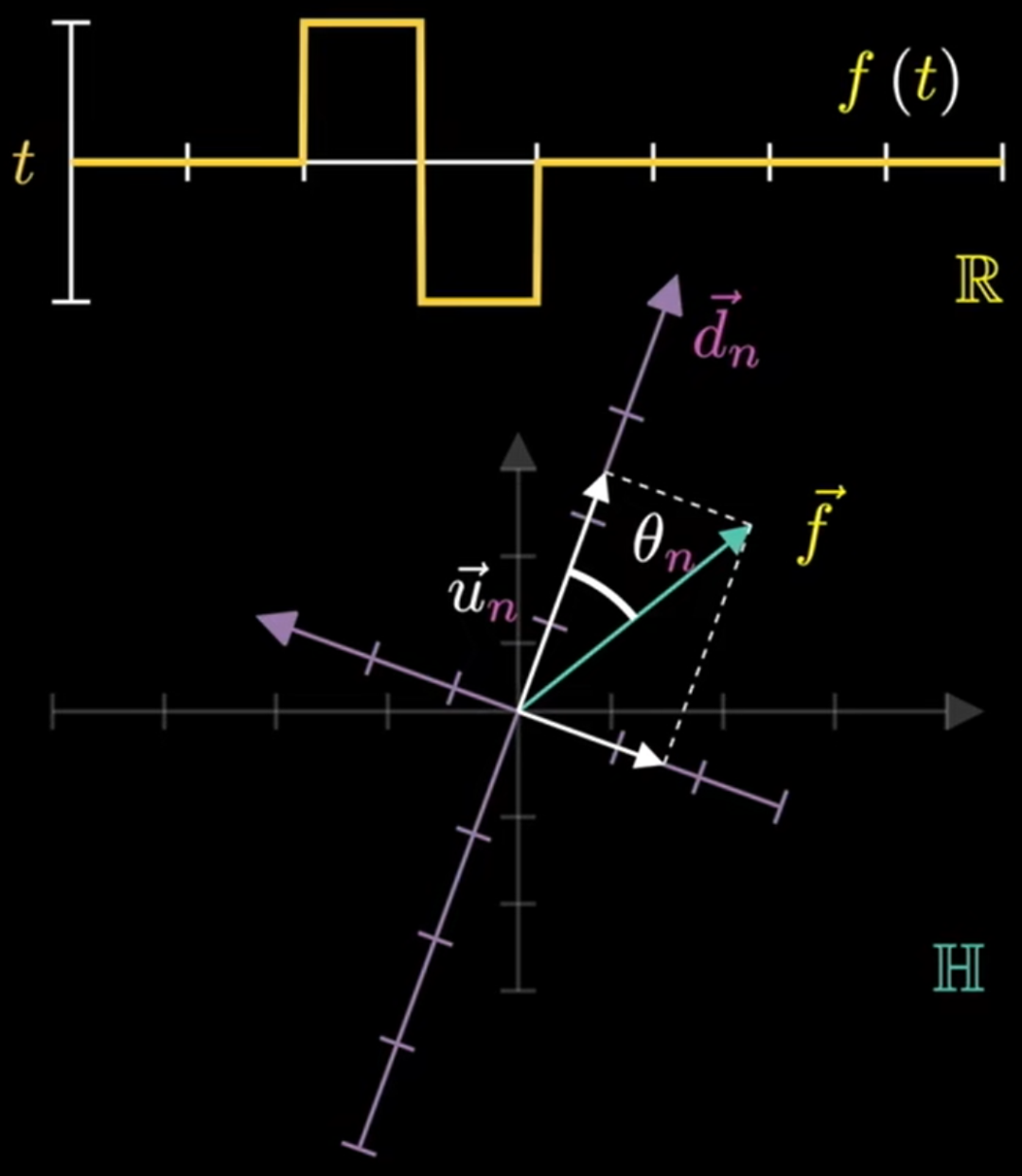
现在考虑无穷维空间中的坐标系变换，向量 在新坐标轴 上的投影为：

由于希尔伯特空间是欧式空间的一个拓展，很多在欧氏空间具有的性质在希尔伯特空间也得到保持。欧式空间中两个向量的内积可以写成两个向量对应元素相乘再相加的形式：

那么，两个无穷维空间中的两个向量的内积 可以写成：

在希尔伯特空间，坐标值的乘积可以写成函数值的成绩。那么，向量 在新坐标轴 上的投影可以写为内积的定积分乘以坐标轴的单位向量：

坐标轴的单位向量可以看作是特征向量或者模式，而坐标值可以看作是这个特征向量对应的特征值。

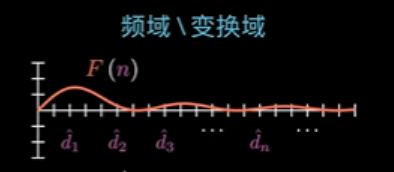
向量 对应到一个二维坐标系（变换域）下，可以用一条函数曲线 来表示。这个函数 表示为：

这个变换域其实就是频域，也就是从时域到频域相当于做了一个希尔伯特空间的坐标转换。频域里的变换就是这个代表特征值的定积分。 代表向量 在新坐标轴 下的坐标值。 与该坐标轴的单位向量 相乘即表示其在该坐标轴上的分量。把在各坐标轴上的分量相加即可得到向量 ，这就是希尔伯特空间的坐标转换的逆过程：

傅里叶变换

把变量 用 表示，坐标轴 用一组 表示，则可得：

上式即为傅里叶变换的过程。

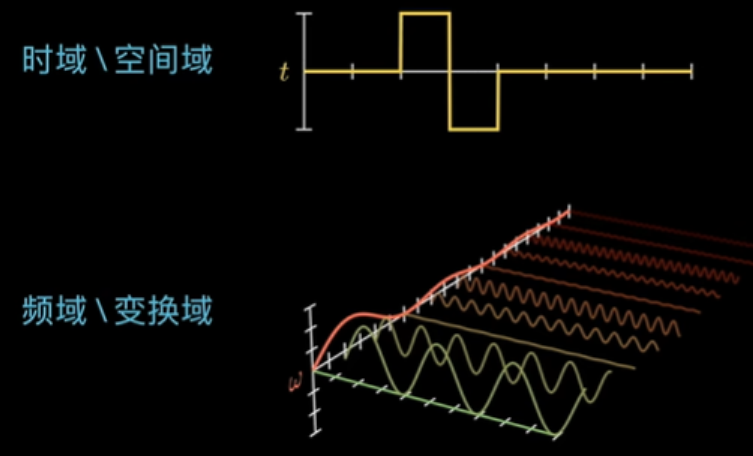
由此可见，傅里叶变换其实就是在希尔伯特空间做的一次特殊的坐标系变换，这组坐标系（基）选择的是 ，其特殊之处在于这组基向量是正交的。

由于负数的模 可以表示为：

则将无穷小量 看作是微分 ，求和符号可以写为积分符号，则：

上式即为傅里叶变换的逆过程。

推广

以上将傅里叶变换和希尔伯特空间中的坐标变换联系到一起，如下图所示：

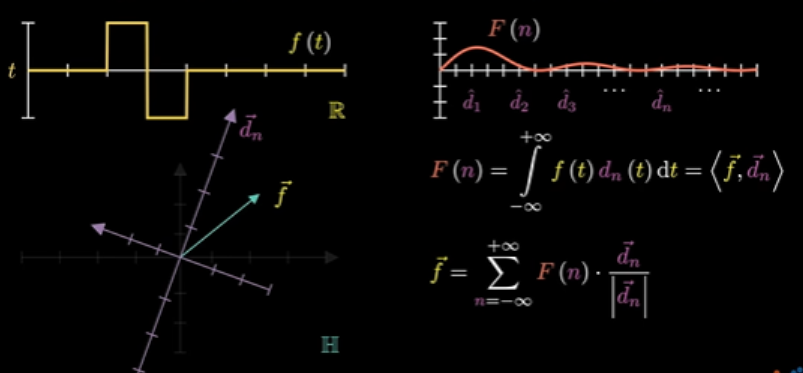
傅里叶的基即新的坐标轴也对应着时域中的一条曲线，即正弦曲线。由于正弦函数曲线是全局的，因此傅里叶变换考虑的主要是全局的变换。以它们作为基元，提取的特征自然是全局特征。

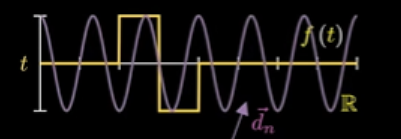
现在考虑对这组基做一些改变，让它们能够体现局部性质。最简单的做法就是对其加窗，让其只在一个范围内进行波动。

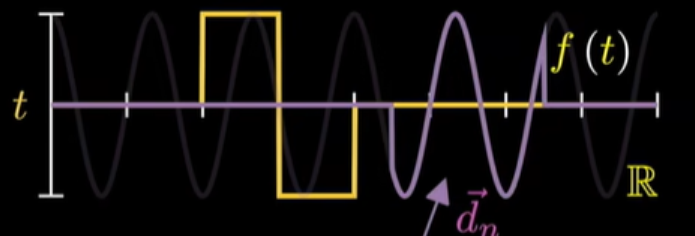
窗口的位置和窗口里边信号的频率都对应不同的坐标轴，窗函数 可以表示为：

考虑窗函数可微，则可选择高斯函数作为窗函数：

其中， 表示方差， 表示期望。

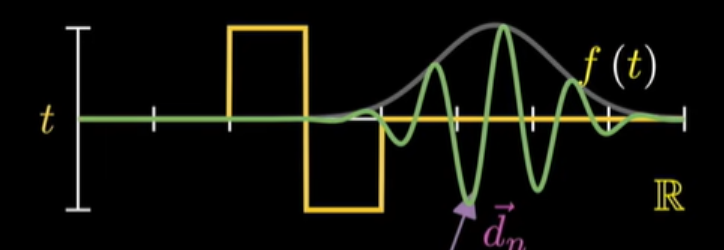
用高斯函数做窗函数的变换就是 Gabor 变换，经过变换后的特征函数分别由 控制频率、 控制窗口位置。

• 当 函数是指数函数时，此时对应的时对应拉普拉斯变换。

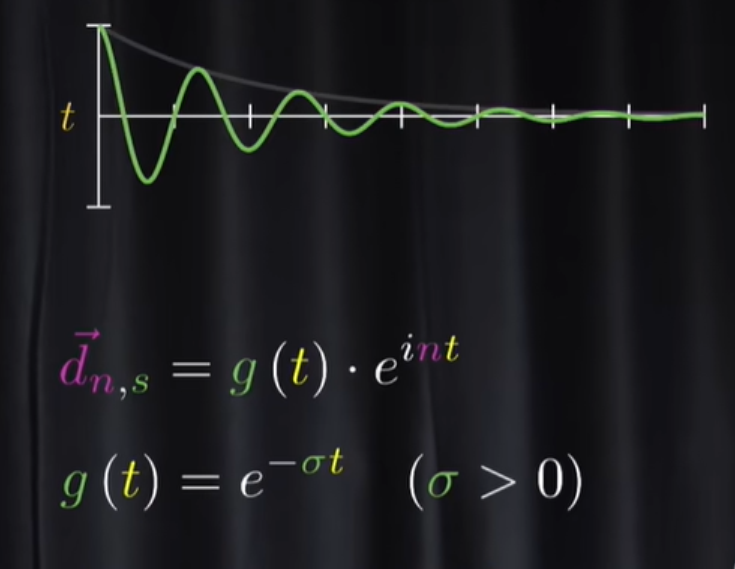
• 当窗口大小可以动态变化时时，此时对应的时对应拉普拉斯变换。

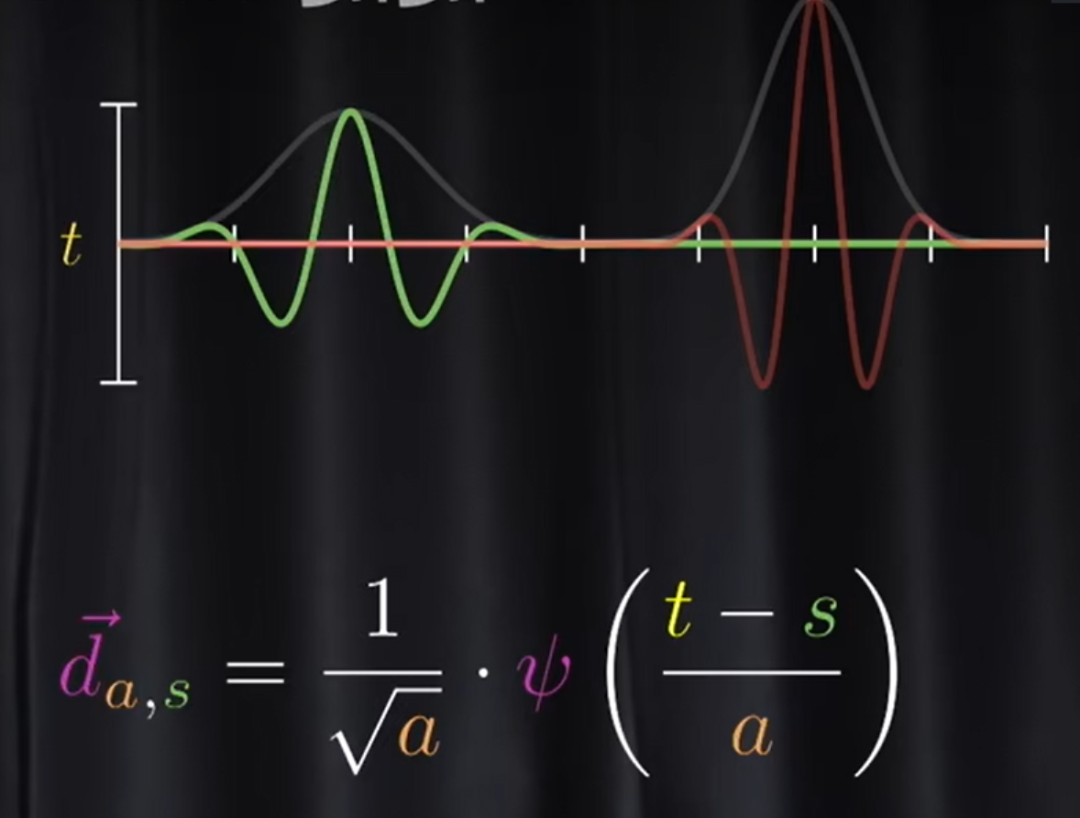
当然，这组基 也可以由其它波形来替换。

这些不同的变换本质上就是在希尔伯特空间里选择不同的基，然后对原来的函数进行的变换。

参考资料